Plan principal – Plans principaux
Plans principaux : explications
Les plans principaux d’un système optique sont utiles pour étudier de manière simplifiée le comportement de ce système destiné à réfracter la lumière, tout comme les points cardinaux, dans des conditions paraxiales. Ils servent à établir un modèle simplifié qui permet de prédire le trajet des rayons lumineux à travers un système optique : ce système peut être simple (une lentille mince) ou plus complexe : lentille épaisse, ou assemblage de lentilles. Les plans principaux n’ont pas d’existence physique: ils sont une construction théorique destinée à simplifier le problème du trajet des rayons lumineux au sein d’un système optique, dans des conditions paraxiales.
Si l’on connaît la position des plans principaux du système optique, on peut en prédire le comportement vis à vis des rayons proches de l’axe optique, c’est-à-dire la direction qu’emprunteront ces rayons après réfraction par le système (au moins dans des conditions paraxiales).
On distingue deux plans principaux : l’un est appelé plan principal objet, l’autre est appelé plan principal image. Cette page a pour but de démystifier le concept des « plans principaux » et des « points cardinaux », qui apparaissent souvent comme assez « ésotériques » pour les non spécialistes !
Justification des plans principaux
Le problème sous-jacent, qui justifie le recours à ce modèle tient à l’ « épaisseur » des systèmes optiques. Il y a deux situations particulières, pour lesquelles le problème est relativement simple :
1) Le système possède une épaisseur infinie : cas du dioptre sphérique. Dans ce cas, le rayon est réfracté, selon la loi de Snell, et poursuit indéfiniment course au sein du dioptre.
2) Le système possède une épaisseur nulle ( infime, que l’on peut négliger en pratique) : cas de lentille mince, idéale. Dans ce cas, le comportement du rayon est prédit par la théorie des lentilles minces (il suffit de connaître la position des foyers de la lentille)
Cependant, quand l’épaisseur du système est intermédiaire (et qu’il est constitué par une lentille épaisse, ou plusieurs), le chemin emprunté par le rayon lumineux est plus difficile à prédire.
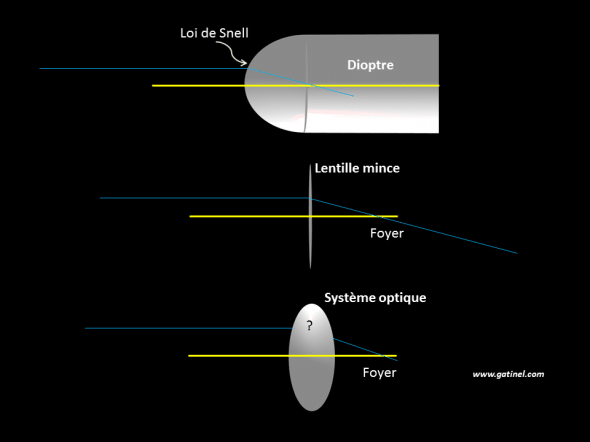
En haut, la loi de Snell permet de prédire le trajet du rayon réfracté (en bleu) par un dioptre sphérique (l’axe optique est en jaune). Au milieu, si l’on connait l’emplacement du foyer objet de la lentille mince, on peut déterminer le trajet du rayon lumineux. En bas, le système optique est « complexe » (ex: lentille épaisse) et il faut tenir compte de l’épaisseur traversée par le rayon lumineux: celui-ci émerge du système à une hauteur différente que celle d’entrée du point incident.
Les rayons incidents parallèles à l’axe optique subissent deux réflexions successives:
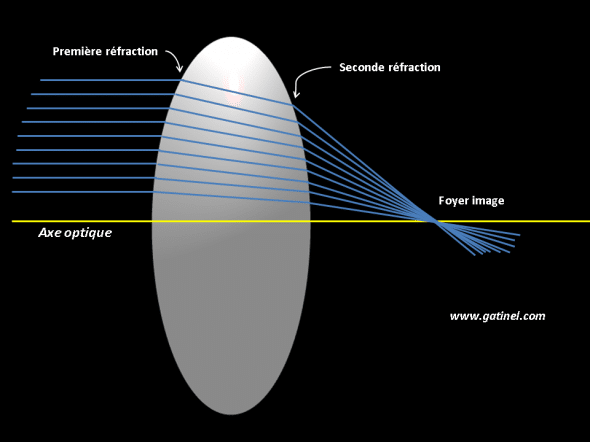
Les rayons lumineux incidents (à gauche) proviennent d’une source distante (à l’infini) et rencontrent la surface gauche de la lentille épaisse, où ils subissent une première réfraction. Les rayons réfractés se propagent alors en ligne droite puis rencontrent la surface droite de la lentille où ils subissent une seconde réfraction, et sont focalisés vers le foyer image. Pour effectuer le tracé géométrique exact et le calcul du trajet de la lumière à travers la lentille (ex : ray tracing), chaque rayon incident engendre deux calculs de réfraction consécutifs (correspondants à la première et la seconde réfraction).
Pour certains rayons particuliers, on peut déterminer facilement le point de sortie ainsi que l’angle de sortie : les rayons parallèles à l’axe optique donnent naissance à des rayons émergents qui traversent tous le foyer image.
Dans le cas d’une lentille mince, on peut faire comme si le rayon parallèle incident était dévié de manière « instantanée » vers le foyer. La hauteur du rayon d’entrée est égale à la hauteur du rayon de sortie. Dans le cas d’un système plus complexe, il y a un trajet « à l’intérieur » du système que l’on ne peut pas négliger : il est responsable d’une variation de la hauteur à laquelle émerge le rayon. La seule certitude est que le rayon émergent issu d’un rayon incident parallèle à l’axe optique passe par le foyer image.
Il est probable que la lumière emprunte le chemin optique le plus « court » entre son arrivée dans le système et sa sortie ; il serait certainement possible de calculer ce chemin, si l’on connait la géométrie du système et ses indices de réfraction, mais il est plus simple de définir l’existence de deux plans, appelés principaux, qui matérialisent l’intersection entre les rayons incidents (respectivement émergents) parallèles à l’axe optique et les rayons émergents (respectivement incidents) qui passent par le foyer image (respectivement objet).
Tracé des plans principaux
Tout se passe alors « comme si » un rayon lumineux incident n’était pas dévié… jusqu’à ce qu’il rencontre le plan principal image : il est alors réfracté vers le foyer. De même, en utilisant le principe de réversibilité du chemin de la lumière, on peut établir qu’un rayon traversant le foyer objet se propage sans déviation jusqu’à rencontrer le plan principal objet, et être alors dévié instantanément dans une direction parallèle à l’axe optique. Ce principe est utilisé pour « tracer » l’emplacement des plans principaux.
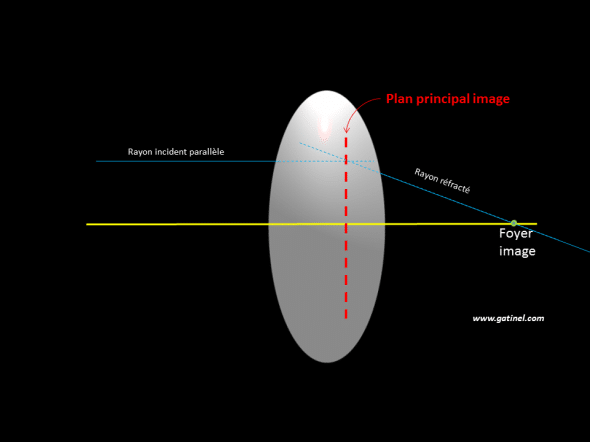
Pour déterminer l’emplacement du plan principal objet, il suffit de tracer un rayon incident parallèle à l’axe optique et de connaître le trajet du rayon émergent (qui passe au foyer image). On prolonge le trajet de ces rayons et leur intersection se fait dans le plan principal image, qui est (en conditions paraxiales) perpendiculaire à l’axe optique.
Si l’on répète ceci pour plusieurs rayons incidents parallèles à l’axe optique, on obtient le tracé suivant :
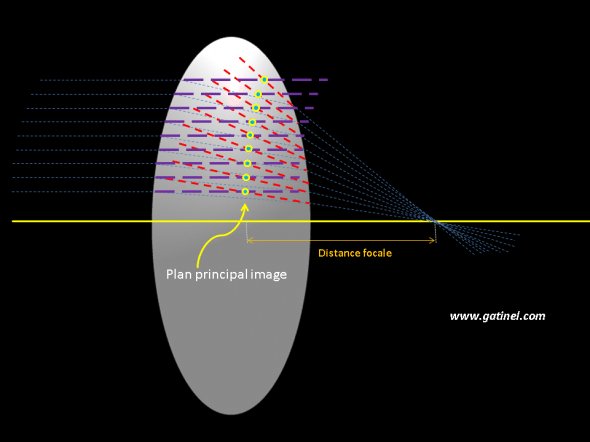
Sur cette figure on a prolongé en pointillés les rayons incidents (en violet) et les rayons émergents (en rouge). L’intersection de ces tracés pointillés vue en coupe (cercles jaunes) définit le plan principal image, qui permet de simplifier le tracé et le calcul des rayons réfractés par la lentille épaisse. Il est intéressant de noter que l’enveloppe de ces points est une ligne droite (un plan) à proximité de l’axe optique, soit dans les conditions paraxiales: à distance, cette surface est légèrement courbe. Le concept de plan principal ne s’applique que dans des conditions paraxiales. L’indice de réfraction de la lentille dépend de la longueur d’onde des rayons considérés.
Pour un indice de réfraction donné de la lentille épaisse, il est possible de définir un plan principal image, et un plan principal objet en raisonnant de manière symétrique.
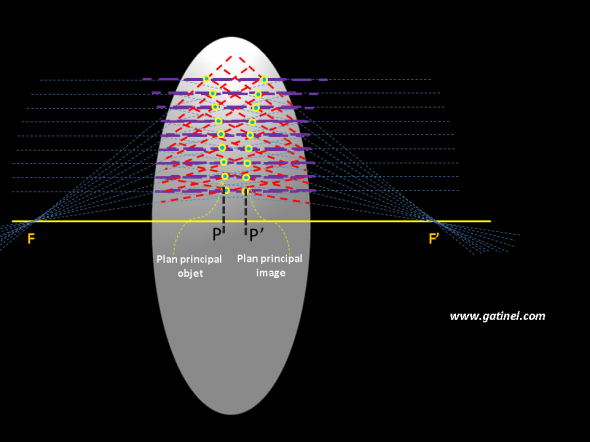
On obtient par la même méthode l’emplacement du plan principal objet. Si la lentille épaisse est située dans l’air, le plan principal image est à une distance identique du centre de la lentille que le plan principal objet.
Si la lentille épaisse est située dans l’air, le plan principal image est à une distance identique du centre de la lentille que le plan principal objet. Quand on étudie un système où le milieu incident possède un indice de réfraction différent de celui du milieu ou se forme l’image (c’est le cas de l’œil), alors cette symétrie disparait, et l’on doit recourir à d’autres constructions théoriques comme les points nodaux pour caractériser le trajet des rayons lumineux paraxiaux.
Au terme de cette construction, on peut considérer que l’on a ramené le système optique « complexe » à un système simplifié, qui serait équivalent à une lentille mince si l’on supprimait l’espace entre les plans principaux objet image (en « pliant » l’espace pour les superposer).
Le grandissement d’un objet situé dans le plan principal objet ( objet virtuel dans le cas où ce plan principal objet est dans la lentille ou le système optique) est égal à 1: l’image correspondante (virtuelle et située dans le plan principal image) est de taille et d’orientation identique à celle de l’objet.
En réalité les plans principaux ne sont réellement plans qu’au voisinage de l’axe optique, c’est à dire en conditions paraxiales: si l’on étudiait plus à distance la forme réelle des surfaces regroupant les points dont l’image par le système optique ne subit pas de magnification et est orientée comme l’objet on observerait des surfaces légèrement courbées.
Les points principaux correspondent à l’intersection entre plans principaux et l’axe optique.
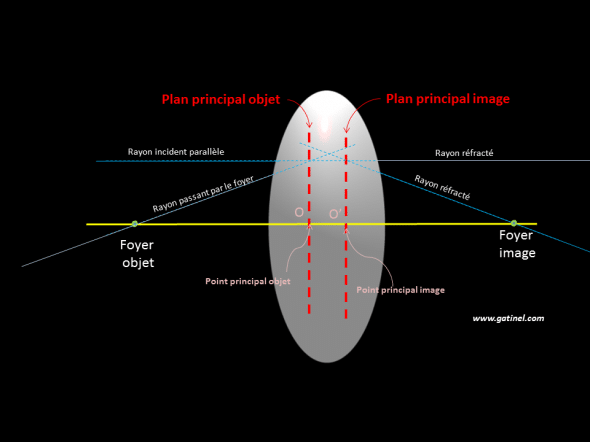
Un tracé similaire peut être effectué pour le rayon incident passant par le foyer objet et réfracté parallèlement à l’axe optique, afin de trouver le plan principal objet. L’intersection entre les plans principaux et l’axe optique définit les points principaux. La distance focale doit être mesurée depuis l’un de ces points jusqu’au foyer correspondant, et non depuis le sommet de la lentille ou du système optique (OF : distance focale objet et O’ F’: distance focale image).
Ainsi, plutôt que de calculer le trajet de chaque rayon incident (ex : ray tracing), il est préférable de remplacer le système complexe (lentille épaisse) par un système simple, constitué de points cardinaux : foyers, points principaux et points nodaux.
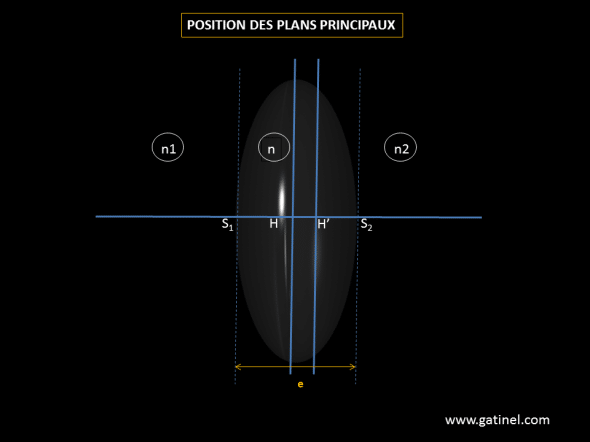
Position des plans principaux
Pour obtenir la position des plans principaux d’une lentille épaisse dans l’air, il faut utiliser la formule suivante, qui donne la distance entre le plan principal de la lentille épaisse et son sommet (ou vertex, intersection avec l’axe optique de la surface de la lentille):
Distance du sommet au plan principal objet ou image
Le schéma suivant permet de localiser les points et dimensions d’intérêt:
1) Distance du sommet avant (S1) au plan principal objet H (distance S1H)
S1H= e x (n1 /F) x (F2/n) où:
F est la puissance focale du système épais centré, n1 l’indice de réfraction du milieu du rayon incident, e l’épaisseur de la lentille, n l’indice de réfraction de la lentille et F2 la puissance de la face opposée (face de sortie).
F2 = (n2-n)/R2 où R2 est le rayon de courbure de la face arrière (passant par S2)
F est calculé selon la formule de Gullstrand, qui tient compte de la puissance de la face avant de la lentille (F1), de la puissance de la face arrière de la lentille (F2) et de l’épaisseur (e) de la lentille ainsi que son indice. F = F1+F2 – (e/n)F1F2
2) Distance du sommet arrière (S2) au plan principal image H’ (distance S2H’)
S2H’= e x (n2/F) x (F1/n) où:
F est la puissance focale du système épais centré (comme calculé plus haut), n2 l’indice de réfraction du milieu du rayon émergent, e l’épaisseur de la lentille, n l’indice de réfraction de la lentille et F1 la puissance de la face opposée (face d’entrée).
F1 = (n-n1)/R1 où R1 est le rayon de courbure de la face avant (passant par S1)
Les courbures des faces avant et arrière de la lentille épaisse, les variations d »indice de réfraction des milieux influent logiquement sur la position de chaque plan principal.
Des pages sont consacrées au calcul des plans principaux de la cornée, et au calcul des plans principaux du cristallin.
Si la lentille a une géométrie asymétrique (comme la plupart des implants intra oculaires utilisés en chirurgie de la cataracte), on ne peut donc identifier la position des plans principaux à celle du centre de la lentille, ou supposer que ces plans principaux se situeront à égale distance du centre de l’implant.
Plans principaux et implants
Les implants de cristallin artificiel sont des lentilles non minces (à leur échelle): afin d’améliorer le contrôle de la réfraction après implantation, et établir des comparaisons fiables en terme de positionnement, il est important que la position d’un implant donné soit mesurée depuis son plan principal objet. La position du plan principal objet vis à vis de l’implant ne dépend pas de sa position effective dans l’oeil (il dépend des caractéristiques de l’implant et des milieux adjacents), mais l’effet réfractif de l’implant dépend de sa position effective (ELP : effective lens position) (c’est à dire non pas simplement la position anatomique de l’implant dans l’oeil après la chirurgie de la cataracte, mais la position de ses plans principaux).
On pourrait repérer la position de l’implant comme la distance entre le sommet de la cornée et le sommet de l’implant, mais étant donné les différentes géométries, indices de réfraction, etc. des implants, ce choix exposerait à des incertitudes quant aux relations entre puissance de l’implant (vergence) et position de celui-ci. La position du plan principal objet de l’implant définit en effet la position effective de l’implant. C’est en revanche depuis le point principal image qu’est définie la longueur focale de l’implant (cette longueur est égale à la distance entre le point principal image et le foyer image).
Les différences de position des plans principaux vis à vis de la géométrie de l’implant expliquent en partie les valeurs de « constante A » (formule SRK T) ou les valeurs des constantes nécessaires au calcul des formules de biométrie (Haigis, etc.).
La position du point principal image et celle du plan principal objet peuvent être calculées grâce à la formule citée précédemment (si l’on connait la géométrie de l’implant : puissance, courbure des surfaces, indice de réfraction, épaisseur de l’implant, et en remplaçant le chiffre 1 qui est l’indice l’air par la valeur de l’indice de l’humeur aqueuse soit 1.333)
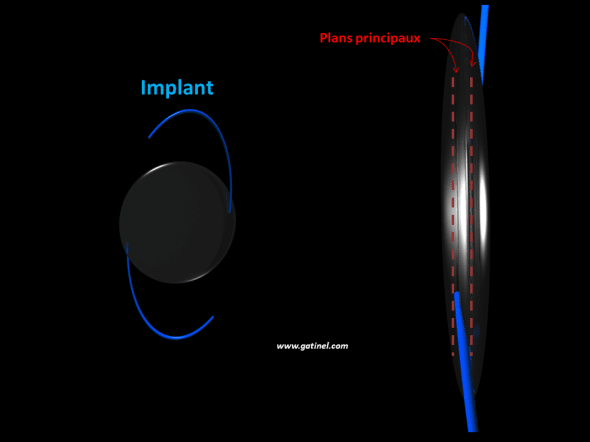
Les implants de cristallin artificiel ont une épaisseur non négligeable: il est important de tenir compte des caractéristiques comme l’épaisseur physique, la courbure antérieure et postérieure de l’implant, et l’indice de réfraction, pour calculer la position de leurs plans principaux, pour repérer de manière optique et fonctionnelle la position effective de l’implant.
Relation de Newton
La construction des plans principaux est faite en utilisant les propriétés des rayons paraxiaux parallèles à l’axe optique, mais une fois ceux-ci connus, il devient possible de prédire la position de l’image formée par le système optique d’un objet.
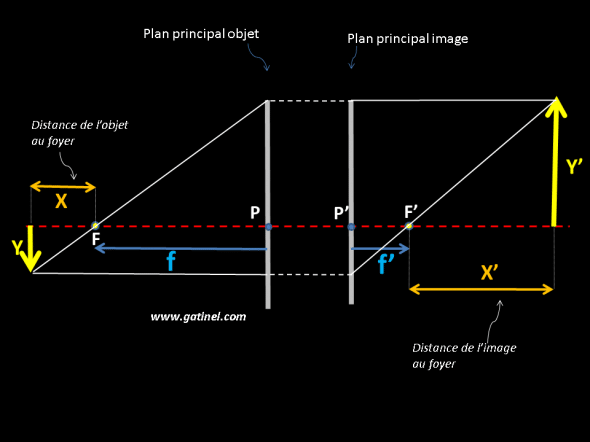
L’utilisation des propriétés géométriques de la figure permet d’établir la relation de conjugaison de Newton. X correspond à la distance de l’objet au foyer objet, X’ correspond à la distance de l’image au foyer image.
L’utilisation des propriétés liées au triangles similaires permet d’établir:
Y’/Y = -F/X = -X’/F’: ces valeurs sont égales au grandissement (magnification) produit par le système optique.
Le signe négatif devant F est lié au sens positif qui est dirigé vers la droite (F, distance du plan principal objet au foyer objet) est dirigé vers la gauche.
On obtient de l’équation précédente que : F F’ = X X’
Le produit des distances focales est égal au produit de la position de l’objet et de l’image !

Bonjour j’ai un exercice d’optique géométrique à réaliser, c’est un système simple où dessus j’ai seulement l’axe optique, des foyers secondaires (AB et A’B’). Il faut que je trouve les plans principaux ( H et H’ et ils sont confondus ) le système baigne dans l’air donc n et n’ valent 1. Je ne trouve pas la solution et nous ne l’avons pas vu en cours pourriez vous m’aider ?
En théorie, aucun impact car le modèle étant paraxial, l’asphéricité n’exerce pas d’influence sur la courbure apicale des éléments considérés. En pratique la situation est légèrement différente car la réfraction est dominée par l’optique paraxiale mais non exactement superposable cependant.