Fréquence spatiale
Une fréquence spatiale est un réseau composé de bandes alternativement sombres et lumineuses, orientées de façon variable. C’est un motif élémentaire qui permet d’étudier le contraste de l’image rétinienne (la fonction de transfert de modulation ou MTF correspond à la manière dont chaque fréquence spatiale voit son « contraste » atténué en fonction de la qualité optique de l’oeil).
Le nombre de paires de bandes sombres et claires (une paire = un cycle) par unité de distance angulaire définit la valeur de la fréquence spatiale (ex : 10 cycles par degré).
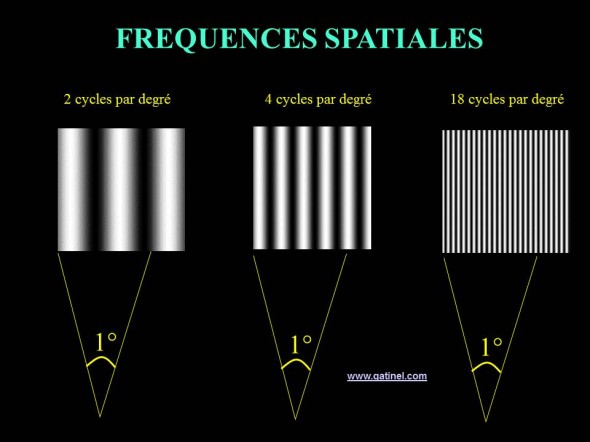
Exemples de fréquences spatiales. Elles sont définies par le nombre de cycles qu’elles permettent d’inscrire dans un degré d’angle. Plus ce nombre est élevé, et plus ces fréquences codent pour des motifs fins au sein de l’image dont elles représentent les « constituants élémentaires ».
Pour percevoir une fréquence spatiale de 30 cycles par degré, il faut un pouvoir de résolution (angle de résolution minimal) d’une minute d’arc, soit une acuité visuelle équivalente de 10/10e. Une fréquence spatiale présente un profil sinusoïdal ; le passage de la région la plus brillante (luminance maximale) à la région la plus sombre (luminance minimale) s’effectue de manière progressive. L’amplitude de la fréquence spatiale correspond à la différence de luminance entre la région la plus « brillante » et la région la plus « sombre ». Ce profil de luminance diffère de celui d’une fonction « rectangle », qui est composée d’une alternance de bande uniformément sombres et claires.
Le contraste d’une fréquence spatiale est défini comme le rapport suivant :
Imax – I min / (Imax + Imin). Ce contraste est « modulé » (réduit d’un certain pourcentage) par le système optique au moment de la formation de l’image rétinienne. La courbe MTF correspond à la représentation de cette modulation en fonction de la fréquence spatiale considérée.
L’utilisation des fréquences spatiales se justifie pour au moins deux raisons : la première est que la superposition de ces différents réseaux de fréquence spatiale permet de recomposer l’image observée. La seconde est que les fréquences spatiales sont « robustes » au «traitement optique de l’œil ; après réfraction, les fréquences spatiales conservent leur profil sinusoïdal et leur fréquence respective est inchangée. Cependant, leur amplitude est diminuée (modulation du contraste) et leur « position angulaire » décalée. Si l’amplitude d’une fréquence spatiale est réduite à zéro après réfraction, elle « disparait » de l’image rétinienne, qui est alors « appauvrie ». La vision floue d’un amétrope (ex : myopie) est liée à la perte des détails de la scène visuelle au niveau de l’image rétinienne. En termes de fréquences spatiales, on peut exprimer ceci par la perte de fréquences spatiales particulières, «codant » pour les détails en question.
L’image d’une scène observée peut être considérée comme un signal complexe dont la variable est la luminance. N’importe quel signal complexe, peut être décomposé en un ensemble de signaux périodiques élémentaires comme les fréquences spatiales, dont le profil en luminance en sinusoïde se prête parfaitement à ce rôle. La décomposition d’un signal en « fonctions sinus » est au cœur de l’analyse de Fourier. Elle permet de transformer un signal (spatial) en un spectre de fréquences (spatiales). Les principes mis en jeu au cœur de l’analyse de Fourier débordent largement le cadre de la décomposition spectrale d’images.
La perception des fréquences spatiales élevées dépend de la capacité de l’oeil à « voir » les détails d’une image. Ceux-ci ne contribuent pas toujours à rendre intelligible une image; au contraire, filtrer ces fréquences spatiales hautes permet parfois de mieux révéler le sens d’une image, quand celui-ci est porté par les fréquences spatiales basses et moyennes. Certains artistes comme S. Dali ont utilisé ces effets dans leurs tableaux, dont les motifs changent en fonction de la distance d’observation (en s’éloignant, on ne perçoit plus les fréquences spatiales élevées).
L’exemple suivant illustre ce principe:

Le mot ci dessus n’est pas aisément perceptible sans reculer l’écran ou « plisser » les yeux pour voir plus flou (et filtrer les hautes fréquences spatiales qui « brouillent » le graphisme plus simple des lettres utilisées et qui ne fait appel qu’à des fréquences spatiales basses et moyennes).
Un filtrage « logiciel » des fréquences spatiales élevées permet de révéler les lettres constitutives du mot « yeux ».

Aspect de l’image précédente après filtrage « passe -bas » (les fréquences spatiales élevées, qui « codaient » pour les contours dédoublés, ont été retirées).
Un autre exemple de filtrage « utile » est disponible ici.

Laisser un commentaire