1. From light’s speed to Snell’s law
This page is dedicated to the simplified study of light propagation within the eye and the main propagation media of interest in Ophthalmology, such as those constituting ocular tissues. Snell’s law is a fundamental property in geometrical optics and at the origin of the vergence formula.
The vergence formula builds the backbone of all IOL power calculation formulas. We will see how to establish Snell’s law from the elementary properties that govern light propagation.
The essential properties of light
On the scale of the Universe, light moves rather slowly; it takes about 100,000 years to travel through our galaxy, which is just one structure among many within an isolated cluster of galaxies. We will call light the small portion of the light spectrum visible to our eyes. Whatever the frequency of the light wave, the speed is identical for a given propagation medium.
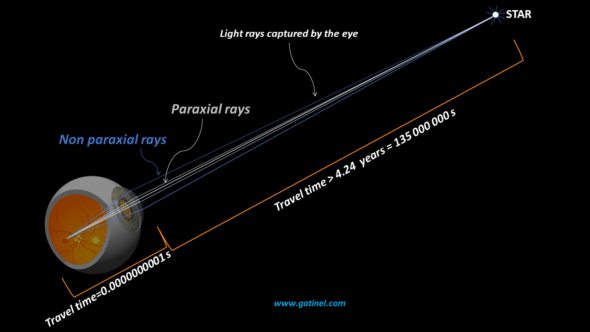
A star in a night sky corresponds to a primary image: the rays emitted diverge from the star in all directions of space. An observer can pick up some of these rays that direct his eyes toward the star. Because of the star’s enormous distance from the eye (the closest star, Proxima Centauri, is located 40,208,000,000,000 km away, and it nearly takes 4.3 years for its light to reach the Earth), the rays picked up are considered parallel. The cornea and the lens must deflect (we speak of « refraction ») these rays toward the retina.
It would certainly be closer to a particular physical reality to consider light emission as a flux of photons in all directions of space. However, in the context of paraxial calculus, the particulate aspect of light is of little interest. The same goes for the wave aspect of light. Still, we will see later that this point is questionable with the notion of the optical path, which connects with the wavefront theory of these considerations on light propagation. Finally, placing oneself in paraxial conditions implies that only the rays which take a path close to the optical axis will be considered: these rays are called paraxial. We can, however, consider that they correspond to the path assumed to be that of the photons picked up by the eye near the center of the pupil.
Light travels at a tremendous speed on our scale, nearly 300,000,000 meters per second. It only takes about 0.0000000001 seconds (100 000 femtoseconds) for light to pass through the eye and travel the distance between the cornea and the retina! It would take even less time if light traveled at the same speed through the eye as through a space vacuum. However, before being absorbed by photoreceptors in the retina, light from the surrounding world passes through transparent ocular media. It slows down (due to interactions with the atomic structures that make up matter).
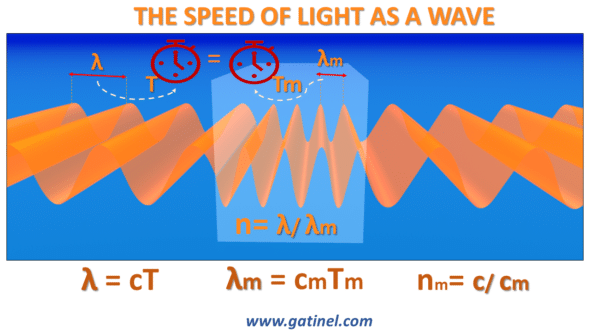
Light slows down in dense material such as the cornea or aqueous humor, but its frequency remains constant. As a result, the wavelength shortens, like a walker whose steps follow the same pace but are shorter.
Specific properties allow simple laws to be established, which are helpful in predicting the path of light through ocular structures:
The speed of light is reduced in dense materials (ex: cornea, aqueous, lens, vitreous) but not its « pulse » (frequency)+++
Therefore, the period (time) (T) elapsing between each crest is constant.
The value of the refractive index (n) of a medium is defined as the ratio between the (length of a) wavelength in a vacuum and the wavelength (of the same frequency) in the medium considered.
The refractive index is also equivalently defined as the ratio between the speed of light in the vacuum and material. However, this definition hides the dependence of the wavelength on the refractive index.
A fundamental property concerns the time taken by light to connect two points. Under the principle of least action, light takes the shortest path in duration (time). This route is not always the shortest from a geometric point of view (distance).
If the travel time of the light information between two points is minimal, the number of unit periods of oscillations is necessarily minimal. The optical path is the length corresponding to the number of oscillations accomplished by the luminous electric field between two points.
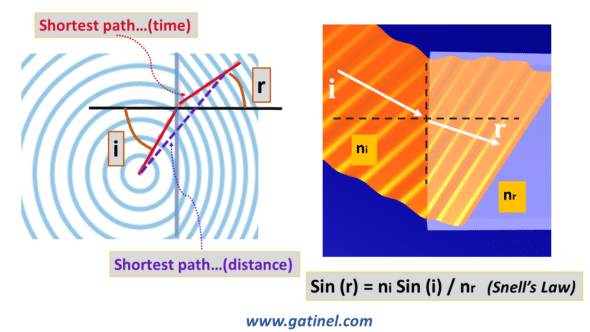
Along imaginary lines locally perpendicular to the wavefront called « rays, »
the geometric distance is not necessarily minimal, but the elapsed light travel time is minimal/. A lifeguard who wants to rescue a swimmer in danger as quickly as possible will have to run rather than swim, but not too much either. Snell’s law provides the solution to finding the optimal route in time.
Snell’s law, shown in the previous illustration, concerns the path of a light ray that encounters a medium with a different refractive index (where light slows down if the refractive index is greater and vice versa). It stipulates that the angle of penetration (we speak of refracted angle, labeled « r ») of this light ray in a given medium is smaller than the angle of incidence (labeled « i ») if the index of this refracting medium (nr) is greater than the index of the medium incident (ni). This happens when light leaves the surrounding air to enter corneal tissue. Conversely, the refracted angle is greater than the angle of incidence at the interface between the corneal stroma and aqueous humor in the anterior chamber.
The angle is defined by the direction normal (locally perpendicular) to the surface at the ray’s penetration point. It is interesting to take a step back because if we think carefully, the behavior of an isolated ray cannot be « understood » without a wave conception of light propagation! We cannot understand how a lone ray « would know » which direction it must take when it changes its propagation medium. Snell’s law is, therefore, not intuitive; on the contrary, it is relatively easy to demonstrate with simple geometric reasoning.
Demonstration of Snell’s law
Snell’s law states that we can calculate the direction of the refracted ray as a function of that of the incident ray if we know the refractive index of each medium (ni for the incident medium, nr for the refracting medium). The angles are related to the line perpendicular to the point of incidence, called the line « normal to the surface. »
Snell’s law can be written simply: ni x sin (i) = nr x sin (r).
Snell’s law is fundamental because it allows the formulation of the vergence formula, so let’s demonstrate it.
In the medium on the left, the wavefront moves at speed vi. On the medium on the right, its speed (vr) decreases. The wavefront forms an angle θi with the normal to the surface and is deflected by an angle θr after refraction. Under Huygens’ principle, the time taken to go from C to B is the same as that to go from A to D. This time is equal to the distance divided by the speed, and we can thus write:
CB / vi = AD / vr
From the geometry of the figure, and by observing that θi is equal to the angle (CAB) and that θi is equal to the angle (ABD), we can express that the distance CB = AB sin (θi) and the distance AD = AB sin (θr)
The preceding equation becomes AB sin (θi) / vi = AB sin (θr) / vr.
We can simplify by AB and multiply both sides of the equation by a constant c (speed of light in vacuum) to obtain: sin (θi) c / vi = sin (θr) c / vr.
The ratio between the speed of light in a vacuum and light in the medium considered is equal to the refractive index of this medium: ni = c / vi and nr = c / vr
We finally obtain the Snell’s law equation: ni sin (θi) = nr sin (θr)
Snell’s law and optical path
Between the two points, the travel time is minimal. It is, therefore, not possible to have fewer unit periods (which correspond to unit paths of one wavelength) between these two points. The minimal number of wavelengths corresponds to the optical path.
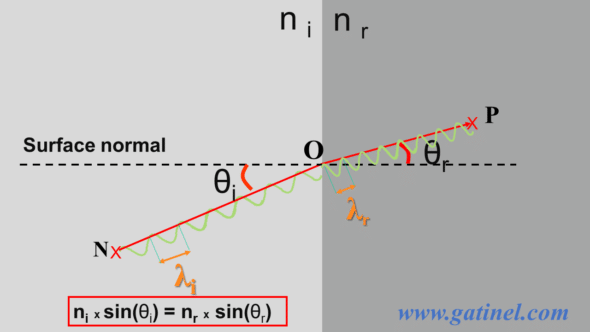
Between the two points, the optical path is minimal: O is such that it is not possible to place fewer wavelengths λi from N and λr to P
if a point receives rays along which the optical path is identical from the source, it is an image point because the light waves will be in phase; they will have accomplished the same number of oscillations from the source and interfere constructively there.
The careful reader will probably have deduced that if one adds a whole number of wavelengths to a given path, the effect will be unchanged. Based on the similarity of the optical path regardless of the whole number of wavelengths added to it, this principle is used for the design of diffractive optics. Thus, these optics must include patterns that make it possible to modulate the optical path by an order of magnitude equal to that of the wavelength. However, these patterns are much smaller than the orders of magnitude used in paraxial optics; the paraxial radius of the anterior face typical of an artificial lens implant measures a few millimeters, while the diffractive steps of bi or trifocal implants have a maximum thickness of a few microns.
Modern biometers use an interferometric method based on the concept of the optical path. Ideally, these methods should consider variations in refractive indices between different ocular components.
The optical path, Wavefront, and Vergence
The concepts of ray and optical path make it possible to understand the rules of geometric optics, the fundamental laws of wavefront propagation, and the notion of vergence. These are practical models that one can select depending on the circumstances.
In cataract surgery, as well as in refractive surgery, specific laws of geometric optics are used. In most cases, the problem relates to that question; where will the image form? For an eye to be emmetropic, the image of a point source, such as a star, must induce an image point located on the eye’s fovea, which captures part of the emitted light.
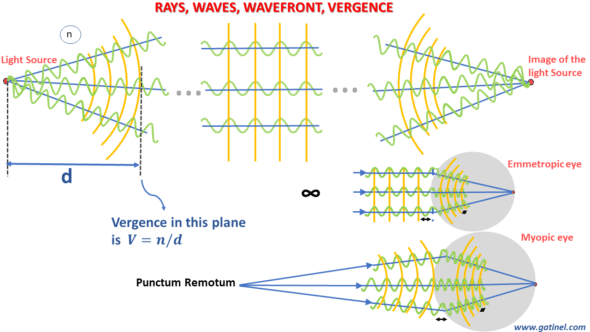
A wavefront is a virtual construction: it corresponds to the envelope of points in space in the same phase whose variations are represented by the wavetrains (sinusoids). In this context, a ray is another virtual construct corresponding to the local direction of propagating the wavefront. When impinging on the eye, the wavefronts diverge from the source and converge through the cornea and the crystalline lens (or the IOL in a pseudophakic eye).
When a wavefront emitted by a near source diverges, then converges after passing through the refractive ocular media towards a point located in the retinal plane, the eye is myopic. The eye is emmetropic when this occurs for a source located at infinity.
The study of the ocular wavefront can be interpreted as the analysis of the differences in the optical path at each point of the pupil, along a path starting from the fovea. The instruments, in fact, carry out their measurement after having emitted a beam of infrared light successively reflected by the fovea and collected at the exit of the measured eye.
The time has come to introduce the notion of vergence. This quantity makes it possible to make predictions relating to the paraxial refraction of the eye. For a point considered, the vergence is the ratio between the refractive index of the propagation medium and the distance remaining to travel to the focal point where the (paraxial portion of the) wavefront converges. This distance is by positive convention when the light propagates and converges to the right. When the light propagates from a source in divergence, the vergence (i.e., the ratio between the refractive index and the distance traveled from the source) is negative.
Why is this ratio between refractive index and distance so important? Because under paraxial conditions (light traveling close to the optical axis), we will see next that we can add or subtract the vergences at each interface to predict where the image will form (i.e., where the rays converge, i.e., where wavefront focuses). If we know the vergence at a given point (and the refractive index of the propagation medium), we necessarily can compute the distance to the next focus if the light does not encounter any other refracting element.


Thank you for your comment, I wish I had the answer to such question! The crystalline lens structure is complex (gradient of index of refraction) and I have no specific information regarding the attenuation of the light flux after it passes the cornea and the lens.
Dear Dr. Gattinel,
Many thanks for this clear and concise overview on electromagnetic waves and lightpath.
I actually came across your website while searching for information regarding crystalline composition and how photons travel through from a quantic physics point of view.
I woud be very gratfeul to you if you were able to share with me any relevant sources of knowledge, if any.
And thanks again for spreading knowledge.
Sincerely, with kind regards,
Erwan Watrin
Thank you Damien to explain so well these basic principles so usefull to understand Light and vision.