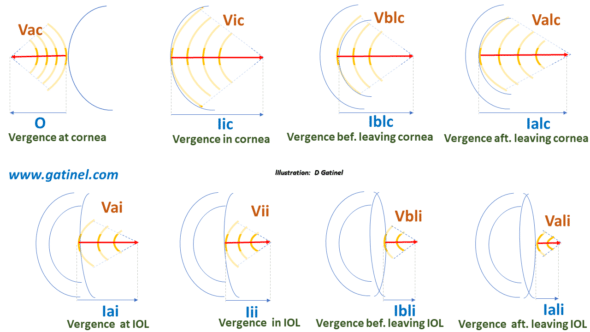
3. Computing vergence in the pseudophakic eye
This page is intended to familiarize the reader with the notion of vergence and its propagation within the ocular media of a pseudophakic eye. From the simplified characteristics of optical interfaces (radius of curvature, refractive index, and separation distances), we will show interactively how one can answer this question: where does the image of a source point focus after passing through the cornea and IOL?
A little reminder on vergence
As we have seen before, vergence is a useful parameter in paraxial optics: it is proportional to the inverse length and is expressed in diopters (D or δ).
We are only interested in part of the light emitted, in the form of wave trains, rays, and wavefronts, but our calculations will focus on vergence.
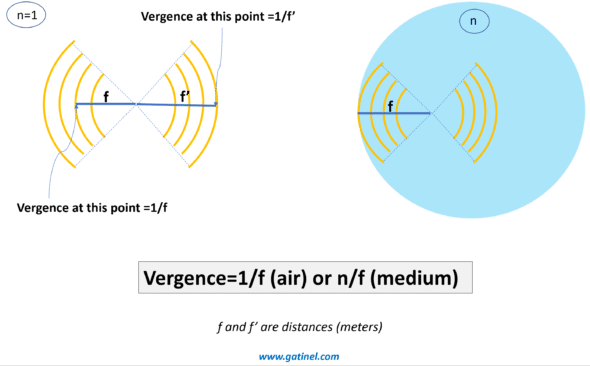
Vergence corresponds to the ratio between the medium’s refractive index and the distance from (negative value) or towards (positive value) the focus.
Let n be the refractive index of the medium considered, and f the distance to the focus:
V = n / f
The vergence of an optical system is positive for a convergent system (light propagates to the right) and negative for a divergent system (light propagates to the left): it takes the same sign as the image focal length.
The further one position is located from the source, the more the vergence decreases (in absolute value). Very far away from the source, we can consider the vergence null.
In the case of an optical system immersed in the air or a vacuum, the vergence can be defined simply as the inverse of the image focal length.
The interest in the concept of vergence lies in the fact that this notion implicitly « contains » the information on the distance from the focus from which the light comes or towards which it converges.
The vergence formula makes it possible to calculate the distance to image focus I after a diopter of radius R and refractive index n’ has refracted the light emitted by a source located at distance O in a medium of refractive index n:
n’/I = n/O + (n’ – n)/ R
n’/ I is the vergence of (to) the image Vi
n / O is the vergence of (from) the object Vo
(n’ – n) / R is referred to as the paraxial optical power P of the diopter.
We can thus write the vergence formula as:
Vo + P = Vi
When we have determined Vi, we know the distance which separates the top of the dioptre from the focus: it is equal to n ‘/ Vi.
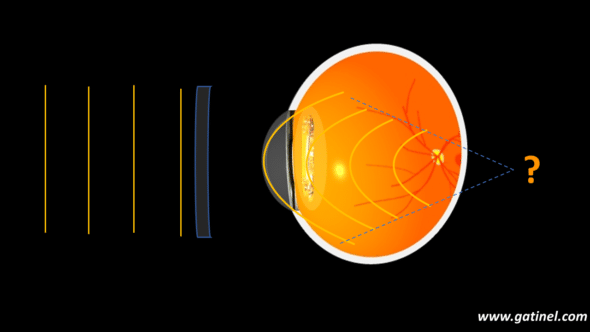
Light propagation to and in the eye
Consider a point source that emits light in all directions. We only represent a part of the light emitted here, in the form of wave trains, rays, and wavefronts, even if our calculations will involve vergence. The diagrams are not drawn to scale, of course.
Suppose a spectacle lens is in the light path far away from the source. When the source is located at a great distance, the portion of the wavefront captured by the spectacle lens can be considered plane and parallel to the axis of the lens. Light propagates in the air (n0=1). The vergence of the wavefront portion (or ray bundle) reaching the spectacle lens is null.
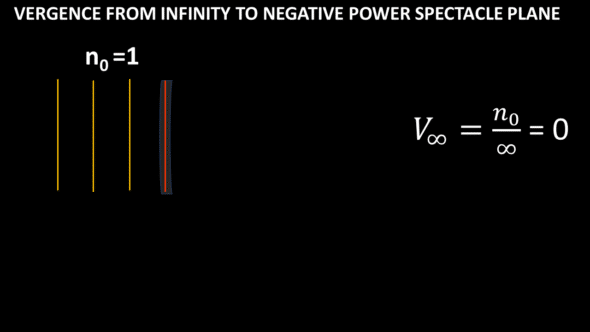
Rays (not shown) are parallel far away from the source: hence, the portion of the wavefront that will be incident on the spectacle glass is flat (i.e., null vergence).
This spectacle glass can modify the path of the light rays. The question asked is: what becomes of the vergence after the passage through the glass?
To answer this question, using the additive properties of vergence suffices. The vergence of a distant source (to infinity) is zero when reaching the spectacle lens. After passing through the glass, the vergence is that of a portion of a spherical wavefront (circular in section) of radius fs. Without any other optical element in the path, this wavefront collapses on its center located at the distance fs. The vergence after the spectacle glass, Vs., is equal to the ratio between the index of the propagation medium (here air, n0=1) and the distance to the focus fs. In this illustrated example, the vergence of the spectacle lens is positive: a beam of parallel incident rays converges a focus after the lens. This beam would diverge in the case of a glass of negative vergence, but the calculation would be the same, except for the sign.
In general, a spectacle lens is placed in front of a phakic or pseudophakic eye, for which it is intended to correct ametropia. The spectacle lens modifies the incident vergence of light so that the image from a distant source is perceived as sharp by that eye, which assumes that this image is formed at the retinal plane. In such a scenario, the vergence of a wavefront that leaves the posterior face of the crystalline lens (or of the IOL if the eye is pseudophakic) is necessarily equal to the ratio between the refractive index of the vitreous and the distance separating the posterior surface of the crystalline lens from the fovea.
To compute the wavefront’s vergence leaving the crystalline lens (or IOL in the case of a pseudophakic eye), we must calculate the cumulative effects on the incident vergence of the eye of the cornea, the lens, and the distance between them and the retina. The method to be applied is always the same: we calculate the vergence at the entry and then at the exit of a refractive element.
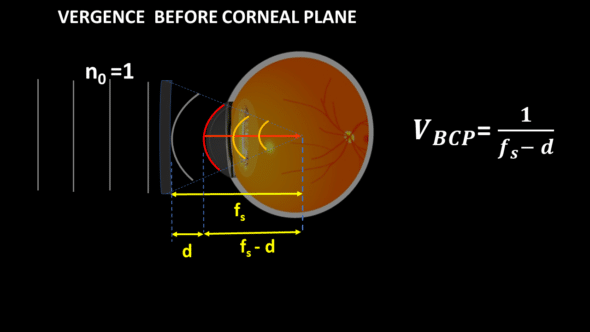
So let’s come back to our spectacle lens. After passing through it, the wavefront propagates towards the cornea, which it reaches after crossing the distance between the spectacle glass and the eye. The vergence just before the corneal plane (VBCP) is, therefore, easy to calculate. We see here that the distance between the spectacle plane and the eye comes into play in the calculation, and we understand why this distance must be considered in the spectacle lens corrections.
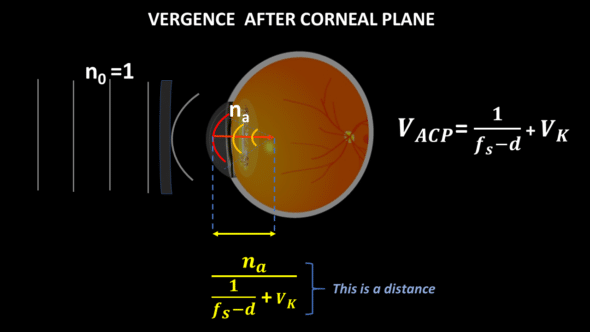
The cornea is considered here as a thin lens. Its vergence (VK expressed in diopter, for example, 43 D) adds up to VBCP, and at the exit of the cornea, the vergence after the corneal plane (VACP) is easy to calculate. After the corneal plane, the distance at which the wavefront would focus in the absence of interposed elements is equal to the ratio between the refractive index of the aqueous humor (na) and the VACP.
We can continue with the propagation of the vergence. The next step is to calculate the vergence in contact with the IOL. It is obtained by first subtracting the distance computed above the distance separating the cornea’s posterior surface from the anterior surface of the IOL. The reciprocal of this distance, multiplied by the aqueous humor’s refractive index, provides the value of the vergence in contact with the IOL.
It is important to familiarize yourself with these gymnastics of calculation used to produce an IOL power calculation formula known as a « thin lens IOL power formula »: it relies on computations using the cornea’s vergence on the IOL considered infinitely thin lenses.
To gain precision in IOL power calculation, it may be interesting to consider the cornea and the artificial lens implant as « thick lenses. » We must then apply the same method as above, detailing the effect of each of the surfaces of the cornea and the intraocular implant. This procedure will make us even more familiar with the vergence formula. It is detailed in the next paragraphs containing an interactive calculation form.
Vergence through a thick pseudophakic eye model
The cornea and intraocular lens (IOL), considered thick lenses, can be analyzed in vergence. The vergence can be traced by noting its change at each surface, using the vergence formula. S1 denotes the plane of the anterior corneal surface, S2 denotes the plane of the posterior surface, and S3 denotes the plane of the anterior surface of the IOL. S1S3 is the anterior chamber depth from the anterior corneal surface.
The distance to the focus is computed from the vergence value (assuming that the light does not meet any other surface and propagates in a medium of the constant index). We subtract from this distance the distance with the next refractive surface to calculate the vergence when reaching this refractive surface.
Each computational step is shown here (not to scale).
We start with a point source located at a finite distance from the cornea: its vergence is negative and equal to the inverse distance. After refraction by the four surfaces of the model eye (front face then back of the cornea, front face then back of the artificial lens implant), the vergence is modified. Its final value makes it possible to calculate the distance to the image focus from the back surface of the implant. If this distance is equal to that which separates the retina from the rear surface of the implant, the retina is said to be conjugated with the source point and will form a clear image of it.
Vergence in the pseudophakic eye: online computation
This spreadsheet calculates the vergences represented in the previous figure, and the distances that separate each incident or emergent wavefront from the next focus. (scroll down for results):
From the thick lens model of the pseudophakic eye, we could estimate, using the vergence formula, the distance between the anterior surface of the cornea and the final focus (referred to as Image Focal Plane in the spreadsheet) for an object located at a distance conjugated with the retina after refraction by the spectacle lens and ocular refractive components. If this distance is equal to its axial length, the pseudophakic eye is well corrected for the distance O.
We can vary the numerical values of parameters such as refractive indices, curvatures, and the distance between the refractive surfaces to appreciate the impact on the focusing distance.
The Coddington factor relates to the design of the IOL and is calculated from the values of the front and back radii of curvature of the IOL. A value of zero indicates that the IOL is symmetrical.
We are now sufficiently familiar with the vergence formula. It is time to discuss its use for calculating the power of the IOL aimed at providing the desired postoperative refraction. Next, we will use the vergence formula to establish a biometric power calculation formula from a thin lens pseudophakic eye model.