Topographie cornéenne : cartes d’élévation

La topographie cornéenne d’élévation permet de recueillir des informations directement relatives à  la morphologie spatiale, c’est-à-dire au relief de la surface cornéenne. La mesure du relief cornéen permet une représentation en élévation, vis à vis d’une surface de référence, qui est le plus souvent sphérique par défaut.

La topographie d’élévation est un outil diagnostique complémentaire à la topographie spéculaire (topographie de courbure). Elle permet d’accéder à l’étude de la face postérieure de la cornée et fournit des informations sur l’épaisseur cornéenne (pachymétrie optique, permettant d’établir une étude de la tomographie de la cornée) qui est déduite de la distance entre les surfaces antérieures et postérieures. Sa généralisation relativement récente a été favorisée par l’essor de la chirurgie réfractive, où elle est particulièrement utile pour la planification de la chirurgie photoablative cornéenne, ainsi que le dépistage des contre-indications au LASIK (dépistage des formes infra clinique débutante de kératocône, comme le kératocône fruste).

Définition de l’élévation en topographie cornéenne

L’élévation dans la topographie cornéenne fait simplement référence à la distance au-dessus ou en dessous à laquelle se situent les points de la surface cornéenne vis-à-vis d’une surface de référence: cette surface est « virtuelle » et doit être calculée. Elle sert simplement de « niveau zéro ». En cela, la topographie d’élévation est plus proche de la notion de « topographie », qui est l’étude du relief des surfaces. La prééminence de la topographie de courbure ne doit qu’à son antériorité historique.

Les données traitées en topographie d’élévation sont directement les coordonnées spatiales de la surface analysée dans un espace à 3 dimensions, et non celle de la courbure locale. La surface cornéenne étudiée y est assimilée à un maillage dont les points possèdent une abscisse X, une ordonnée Y et une coordonnée d’élévation (Z).

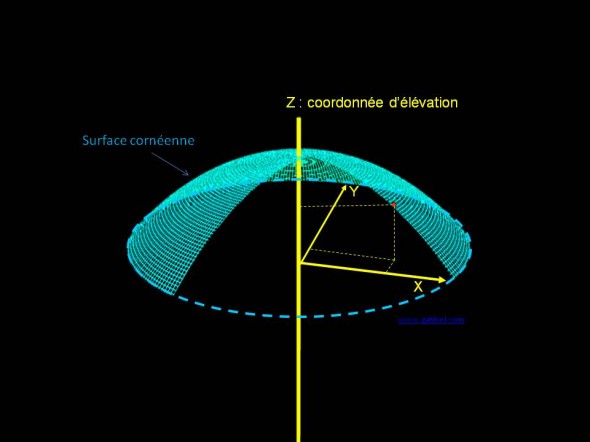
La topographie d’élévation permet d’appréhender le relief de l’élévation de la surface étudiée (antérieure ou postérieure). Les données « brutes » recueillies par les sytème d’analyse (caméra Scheimpflug, balayage par fente, etc…) correspondent à une valeur d’élévation absolue (Z) pour chaque couple de point (X,Y) situés dans le disque plan couvrant le diamètre d’analyse (en général proche de 10 mm). Ces coordonnées sont représentées ici en projection sur les axes (X,Y, Z) pour un point figuré en rouge. A ce stade, la surface de référence n’est pas encore calculée.

Les données d’élévation cornéenne peuvent théoriquement être calculées à partir des données de courbure (technologie de réflexion spéculaire, qui fut la première technique utilisée pour l’étude de la topographie cornéenne). Il faut effectuer une opération mathématique qui induit une perte de précision de l’étude de l’élévation vis à vis de la mesure directe. Acquises de manière plus directe en utilisant les images numérisées du balayage d’une fente lumineuse (instrument Orbscan), ou d’une caméra rotative Scheimpflug (instruments Pentacam, Galilei, TMS 5).

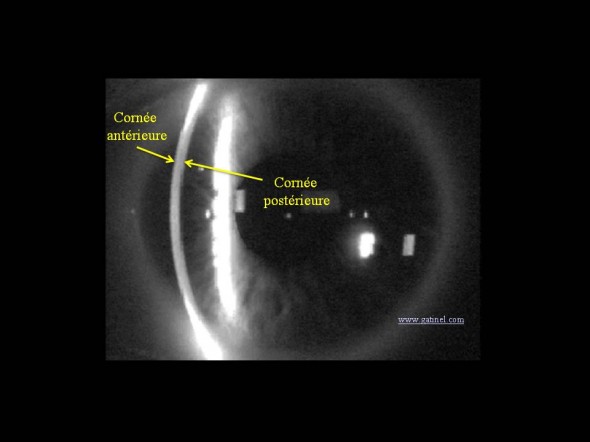
Acuquisition des données brutes de l'élévation par le topographe Orbscan : visualisation d'une des fentes lumiineuses utilisées pour l'acquisition des données antérieures et postérieures de la cornée.

Images correspondant à des images acquises par le topographe Galilei (Ziemer). Ce topographe est équipé d'une double camera Scheimpflug et permet de visualiser le segment antérieur et calculer la topographie d’élévation cornéenne antérieure et postérieure.

L’acquisition directe (indépendante de la technologie par réflexion spéculaire type Placido) est plus fiable que le calcul effectué à partir des données de courbure,car elle n’est pas influencée par l’interpolation mathématique et/ou le lissage des données spéculaires, liés au nécessaire calcul d’intégration pour passer de la courbure à l’élévation. La courbure est en effet déduite de l’élévation, car le rayon de courbure local d’une surface se calcul à partir d’une opération de dérivation (nécessité d’obtenir la pente locale et surtout ses variations; opération de dérivée seconde).

Ce type d’acquisition directe fournit également des données d’élévation de la surface postérieure de la cornée, que les techniques de réflexion spéculaire ne peuvent analyser : en effet, le reflet spéculaire est proportionnel à la différence d’indice de réfraction au niveau de l’interface réflective. n ce qui concerne la surface postérieure et l’humeur aqueuse, cette différence est trop faible pour permettre l’étude du reflet de mires projetées.

Les images des données brutes recueillies par le système de détection (camera Scheimpflug, ou détection de « fentes balayantes ») sont traitées par un procédé mathématique dédié (ex : triangulation) en vue de la reconstruction tridimensionnelle des surfaces de la cornée. Les surfaces antérieure et postérieure de la cornée délimitent le volume cornéen, ce qui permet d’établir un relevé pachymétrique « point par point », permettant alors l’établissement d’une carte tomographique.

Compte tenu de la divergence entre le diamètre total de la cornée (échelle millimétrique) et la variation de l’élévation qu’il faut décrire (échelle micronique), la représentation des variations fines de l’élévation ne peut pas être faite par rapport à une surface de référence (SR) horizontale arbitraire comme un plan.

Comme la cornée, la Terre est un corps dont la surface est proche de la géométrie d’une sphère. En topographie terrestre, le niveau moyen de la mer est commodément choisi comme celui la surface de référence habituelle et « niveau zéro ». Les terres situées sous le niveau de la mer et les fosses sous- marines sont alors pourvues d’une élévation « négative ».

La représentation de l’élévation cornéenne suppose  aussi l’utilisation d’une surface de référence, par rapport à laquelle les différences d’élévation seront caractérisées. Afin de mettre en évidence les petites variations locales, la surface de référence doit épouser le profil global de la surface mesurée. La sphère est la surface géométrique choisie « par défaut » pour représenter l’élévation de la cornée. Il est important de comprendre que la Surface de Référence utilisée pour la représentation de l’élévation de la cornée doit être calculée : elle correspond à une surface géométrique caractérisée (ex : sphère) dont les points sont les plus proches de la surface analysée.

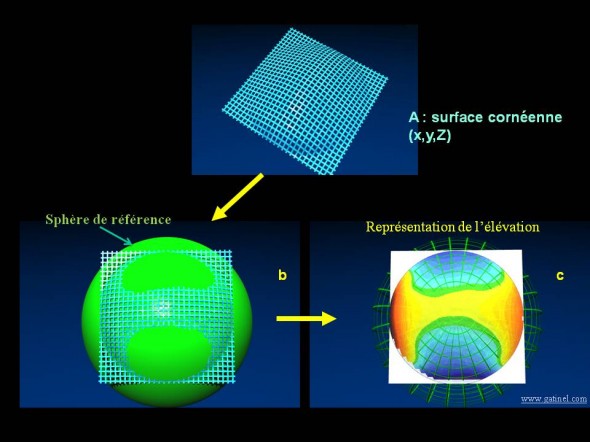
Représentation schématique de la séquence conduisant à la représentation en élévation de la surface de la cornéen. Une fois l’élévation acquise (la matrice des points recueillis est représentée en bleu), une sphère de référence est calculée (b). Une couleur est atrribuée à chaque point en fonction de sa distance à la sphère de référence (c). Les points situés "au dessus" de la sphère sont colorés en couleurs "chaudes", et les points situés "au dessous" en couleurs froides.

Calcul de la sphère de Référence :

Une fois accomplie l’acquisition des données brutes d’élévation (coordonnées X,Y,Z), le logiciel du topographe doit calculer une sphère de référence (communément appelée même en France : « best-fit sphere »: BFS) en utilisant un algorithme approprié. Schématiquement, plusieurs sphères (de rayon et position variable – mode dit « flottant » ) sont « testées » et pour chacune, le logiciel du topographe calcule la somme des distances élevées au carré entre chacun des points de la surface cornéenne mesurée et la sphère pressentie. La sphère retenue est  celle pour laquelle la somme du carré des distances avec la surface cornéenne mesurée est la plus faible. Élever au carré la distance mesurée permet à la fois d’annuler l’influence de la position (supérieure ou inférieure) du point mesuré par rapport à la sphère testée, et de donner un certain poids aux points les plus distants de la courbe testée. La sphère de référence retenue est ainsi celle dont l’écart quadratique à la surface cornéenne mesurée est la plus faible.

Il faut calculer une sphère de référence pour la face antérieure de la cornée, et une autre sphère de référence pour la face postérieure de la cornée: bien évidemment, ces sphères n’auront pas le même rayon.

La valeur du rayon de la sphère de référence n’a pas de signification optique particulière, et ne correspond pas directement à la valeur de la kératométrie moyenne de la surface étudiée, même s’il est en général d’autant plus grand que la kératométrie moyenne est basse. L’asphéricité et le degré de toricité ou d’irrégularité de la surface cornéenne représentée influent également sur le rayon de la sphère de référence. Quand la surface cornéenne analysée est dominée par la toricité, le rayon de la sphère de référence tend à adopter une valeur intermédiaire entre les valeurs respectives de courbure du méridien le plus plat et du méridien le plus cambré. De ce fait, les points situés le long des méridiens les plus plats seront plutôt situé au dessus de la sphère, alors que ceux situés le long des méridiens les plus cambrés seront situés au dessous. Un motif d’élévation en « X » (en « croix ») est alors obtenu.

Rendu des cartes d’élévation :

Après calcul de la sphère de référence sur un diamètre d’analyse donné, les données d’élévation sont rendues en utilisant une échelle de couleurs appropriée. Avec la plupart des topographes et par analogie avec les cartes terrestres d’élévation, les points au-dessus de la sphère (élévation positive) sont représentés en couleurs chaudes, allant du jaune et rouge foncé, tandis que les points situés au-dessous de la sphère (élévation négative) sont représentés en couleurs froides (du bleu ciel au violet). Les points situés au niveau de la sphère sont représentés en vert (« niveau zéro »). E topographie d’élévation, une zone « rouge » doit simplement être perçue comme « au dessus » de la sphère de référence, non comme une zone cambrée.

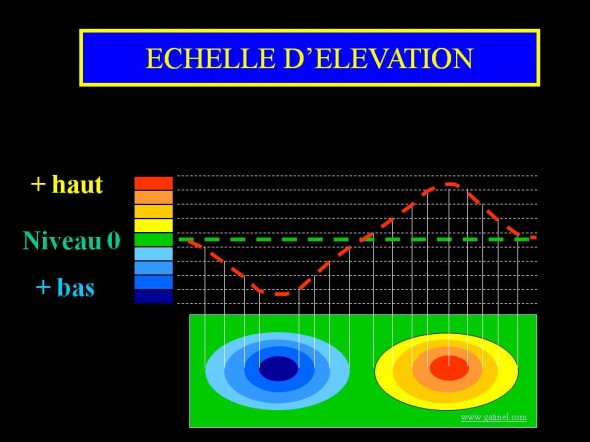
Principe de l’échelle colorimétrique pour l’élévation. L’unité habituelle est le micron. Chaque couleur correspond à un pas, le plus souvent égal à 5 microns par défaut.

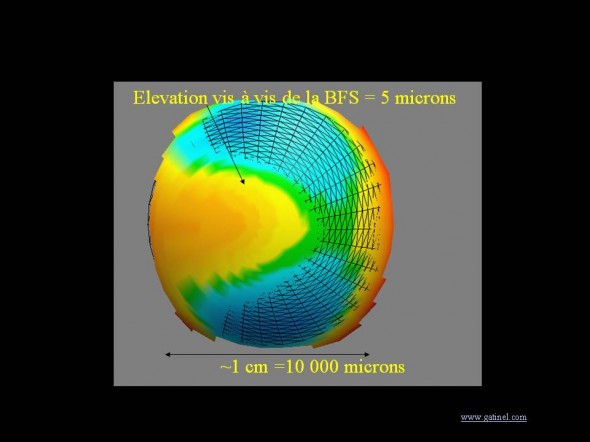
: Représentation en élévation d’une surface antérieure de cornée normale. Les disparités d’élévation vis-à-vis de la sphère de référence (maillage sombre) sont représentées par une couleur différente en fonction de leur valeur. Le pas de l’échelle est ici de 5 microns, et les points situés dans les zones colorées en jaune clair ont une élévation (distance) à la sphère comprise entre 2.5 et 7.5 microns. Les variations de l’élévation sont environ 1000 fois plus petites que le diamètre de la cornée mesurée.

Disposer de l’élévation antérieure et postérieure, tout en connaissant l’écart entre ces surfaces permet de réaliser une carte de pachymétrie, qui fournit un relevé particulièrement exhaustif des variations de l’épaisseur cornéenne: on définit également ce type d’étude comme la représentation tomographique de la cornée. L’échelle de couleur varie des couleurs chaudes (cornées fines) aux couleurs plus froides (cornées épaisse) . La valeur de l’épaisseur minimale, sa localisation, l’existence d’un amincissement central ou paracentral sont autant d’informations recherchées en chirurgie réfractive, dans le cadre du dépistage du kératocône infra clinique notamment.

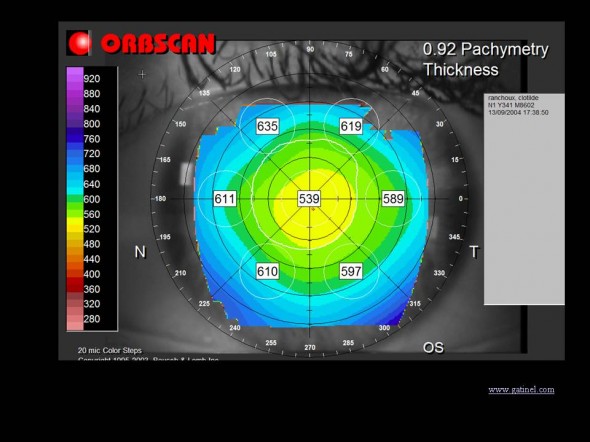
Exemple de carte pachymétrique. L’échelle correspond à la distribution de l’épaisseur en microns. L’emplacement du point le plus fin (« thinnest point ») est matérialisé par le point rouge. Les chiffres présentés sur la cartes correspondent à des épaisseurs moyennes locales.

Contraintes d’alignement

Les différents choix possibles pour l’alignement sont les suivants : « float », « axis », « pinned » ou « apex » (Figure 11). Le mode « float », dans lequel aucune contrainte n’est appliquée à la sphère de référence, est le mode par défaut de la plupart des topographes. L’alignement « axis » contraint le centre géométrique de la sphère à être aligné avec celui de la cornée, avec possibilité de se déplacer le long de celui-ci. La contrainte « pinned » impose une intersection de la sphère de référence et de la surface sur l’axe de visée. Le mode « apex » combine les deux contraintes, celle du mode « pinned » et celle du mode « axis ».

Par défaut, il n’y a pas de contraintes d’alignement pour la sphère de référence (la sphère calculée est dite« flottante », ou encore en calculée en mode « float »‘). Le centre de la BFS n’est pas contraint de se situer sur l’axe géométrique de la cornée, et la sphère choisie correspond simplement à celle qui épouse le mieux la surface cornéenne considérée.

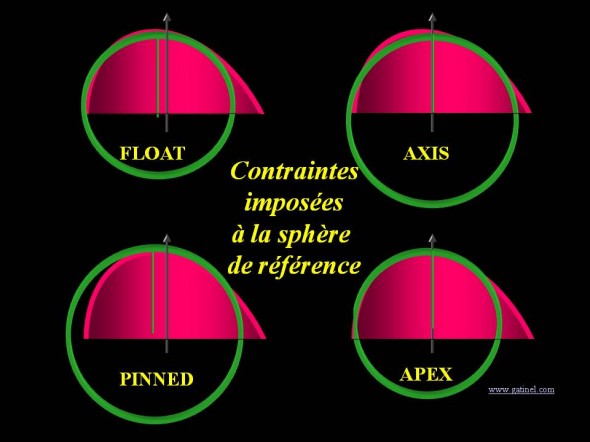
Représentation schématique des différentes contraintes d’alignement possibles pour le calcul d’une sphère de référence. La flèche verticale marque l’emplacement du centre géométrique de la cornée

Surfaces de références non sphériques

Il est possible de sélectionner dans le menu du logiciel de topographe comme l’Orbscan, le Pentacam ou le Galilei une surface de référence NON sphérique. Par défaut, le calcul des surfaces de référence est effectué en mode « float ». Il est également possible de contraindre l’axe géométrique de ces surfaces à s’aligner sur celui de la cornée (ex : mode axial avec l’ Orbscan). L’intérêt des surfaces non sphériques est de mieux « coller » à la réalité géométrique de la cornée, et de permettre de scinder qualitativement l’effet de certaines caractéristiques de la forme de la surface analysée.

En plus des contraintes d’alignement peuvent être ajoutées à la sphère de référence calculée, et d’autres surfaces géométriques de références peuvent être choisies, telles que des ellipsoïdes, des toroïdes ou tout conicoïde.

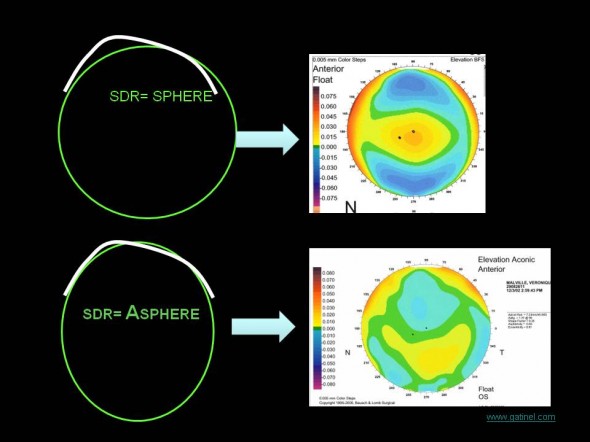
: Principe de l’effet du changement de surface de référence. La cornée étant naturellement légèrement asphérique et asymétrique (en plus de présenter un degré variable de toricité), le choix d’un type de surface de référence exempt (sphère) ou muni d’une ou plusieurs de ces caractéristiques permet souvent de mieux épouser le relief cornéen. De plus, le degré d’asphéricité et de toricité de la surface de référence fournit une « estimation » de celui de la surface cornéenne analysée. A gauche, représentation schématique d’un profil cornéen (en blanc) et sa surface de référence (profil vert). A droite, un exemple de carte d’élévation ou un changement de surface de référence (sphère en haut, et surface aconique en bas) a été effectué. Le mode aconic permet à la surface de référence calculée d’être torique et apshérique. Cette représentation permet de souligner un certain degré d’asymétrie verticale dans le relief étudié. Cette carte correspond à une cornée atteinte de kératocône débutant.