Centering corneal based refractive surgery
Centration (or centering) of the surgical procedures is an important area in refractive surgery. While using the center of the entrance pupil as landmark for large treatment zones such as myopic laser photoablations may be sufficient for achieving good optical quality, smaller treatment zones such as hyperopic photoablations or corneal inlays (ex : Acufocus KAMRA inlay with its central 1.6 mm zone) may be less forgiving (see related article). It is well admitted that the visual axis is NOT coincident with the line joining the fixation target to the center of the entrance pupil (this line is called the called line of sight). Hence, it is of paramount importance to adopt a proper strategy for centering hyperopia and presbyopia related surgical procedures.
To understand this topic, we need to introduce a number of axes, which validity is dependent upon some « idealized » properties of the human eye. While learning some theory cannot be detrimental in essence, the specificities of the eye and some conflicting nomenclature have made this field a bit complicated. There has been a confusing array of terms, which the second part of this page will address. We first need to define the mot meaningful ones in order to answer this simple question: for any corneal refractive procedure (laser photoablation, inlay insertion, femto assisted corneal surgery, etc. s), which the best centration strategy ?
This page and its related links are written for the ophthalmic surgeon, assuming that mastering this topic may allow to obtain better clinical results. We will have to introduce theoretical concepts,but we may try to keep them as simple as possible; and not loose their clinical significance.
Centering strategies based on the vertex normal
For the naive reader centering the refractive correction on the center of the cornea might be a reasonable strategy. Unfortunately, this approach is irrelevant since the cornea is usually not perfectly rotationally symmetrical, and is also slightly irregular. The junction between the cornea and the surrounding conjunctiva (limbus) is not perfectly circular. More importantly, the aperture stop of the eye (iris pupil) is neither aligned nor centered on the corneal dome.
For the impatient reader whose inclination to subtle physiological optics is moderate (or whose life is fulfilling enough so that he would not waist time with it), I will jump to the bottom line, where simple but approximate guidelines can be proposed:
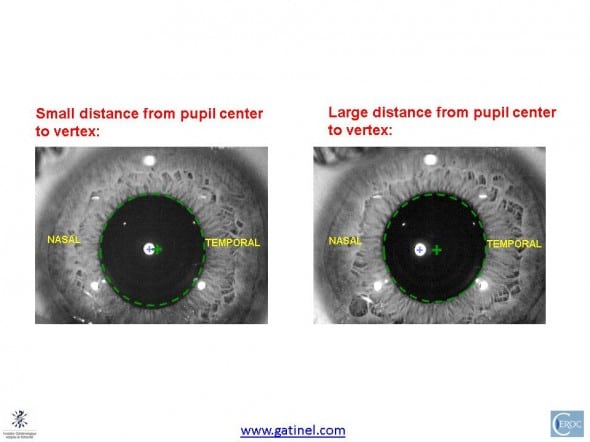
Although partly empirical, following these guidelines will improve the retinal image quality in most cases, especially when the treatments zones are narrow (corneal inlays i.e. Kamra, Intracor (c) , hyperopic LASIK, etc). The distance from vertex to entrance pupil is usually less than 0.3 mm (300 microns) : beyond 0.4 mm, this distance can be considered as large. The proposed strategy aims at trying to reduce the odds of improperly centering the refractive treatment, as the true visual axis intercept location remains speculative, although the results of some studies suggest that it stands between the apparent location of the vertex and the center of the pupil.
In particular, it is important to note that the vertex location is NOT equivalent to the visual axis. The vertex is simply a virtual image formed behing the cornea by the reflective properties of its anterior surface: in another words, the light forming the vertex image (1st Purkinje image) is NOT refracted but reflected by the eye. Its location is aligned with the center of curvature of the anterior corneal surface, but does not relate to the other refractive ocular surfaces (posterior corneal surface, anterior and posterior surfaces of the crystalline lens).
In addition, the visual axis is an idealized concept, which supposes that the eye is rotationally symmetric. Because the lack of symmetry of the eye, the concept of locating the corneal intercept of visual axis can be thought instead as locating a « sweet spot » which should serve as the center of the surgery, in order to optimize the quality of the retinal image.
This page will now expose a short overview of the definitions and concepts which gravitate around the question of the best centering strategies. Because of the eye’s biological basis, different axes must be used to define image formation.
The eye is not rotationally symmetrical about a single axis
If the human eyes were centered optical systems (just as a zoom of a reflex camera, where each of the lenses are centered, aligned and rotationally symmetrical on a common axis, any treatment would have to be simply centered on the corneal geometric center: this center would be confounded with the vertex of the cornea, the optical axis of the eye. There would be one straight line joining the fixation target to the corneal vertex, the center of the entrance pupil, the center of the crystalline lens, and the fovea: actually, this line would be the optical axis.
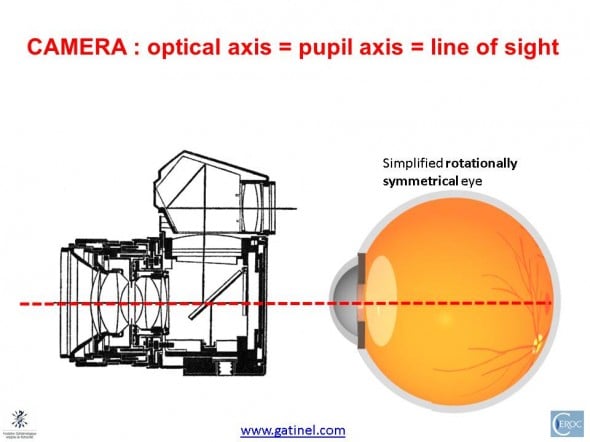
In a symmetrical eye, all refractive surfaces and aperture (iris pupil) are aligned on a common optical axis (as in a reflex camera) : this axis is therefore the landmark for centering corneal based refractive procedures. The vertex (image reflected from a light source coaxial with the optical axis) would be coincident with the visual axis, for geometry reasons.
Unfortunately, as shown here, the cornea, the crystalline lens, the pupil and the fovea are nor centered, neither aligned around a common axis. One may define one « best fit » optical axis, which is a theoretical construction based on the average of each ocular structure’s own optical axis. A method to locate this axis could consist in trying to best align the reflex of the 4 main refractive surfaces of the eye. This would require a special apparatus, which would be sensitive enough to locate the faint reflex of the posterior surface of the cornea and crystalline lens. With regards to this ocular best fit axis, the fovea is slightly displaced temporally in human eyes.
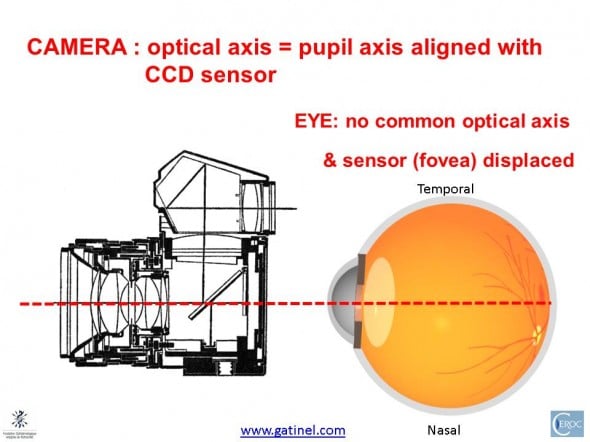
Real human eyes are not symmetrical; the cornea and lens are neither aligned nor centered. One may define the optical axis as the « best-fit » axis between the cornea and the lens (red dotted line). The iris pupil is neither centered nor aligned with the ocular refractive structures, and the optical axis. The fovea is slightly temporal to this « best fit » optical axis. Hence, the visual axis (which will be described later) is usually « piercing » the cornea nasally to the pupillary axis.
Fixation and visual axis
Let us consider a « perfectly rotationally symmetrical » ( theoretical – non real) eye again, where the cornea, lens, pupil and fovea would be symmetrical,aligned and coaxial. This eye is convenient, since its optical axis is the same as its visual axis. Suppose that this eye is oriented to fixate a monochromatic fixation source (F) : it aims at forming a foveal image of the source (F). In this example, we suppose that this source would located in the nasal portion of the visual field.
To fixate the fixation target, the eye will rotate until the retinal image of F is formed on the fovea. At the foveal zone, which is a few tenth of microns wide, the photoreceptors are packed with the highest density, and only represented by the cones. The inner segment of these cones are comparable to small optical fibers, which tend to be oriented toward the visual axis, in order to maximize the change of catching incoming photons. This directional dependance in efficiency has been called the « Stiles Crawford » effect.
In the case of a simplified rotationally symmetrical eye, once the globe has rotated to align the target with the fovea, this would result in a perfect alignment of F, the cornea, center of iris, crystalline lens and fovea.

A perfectly « symmetrical eye » would rotate to align its optical axis onto the Fixation source (F).
In this simplified situation the eye’s optical axis contains both the fixation target and the fovea.
However, in a more realistic eye where there is a temporal displacement of the fovea (but otherwise the same basic corneal and lens power, etc.) , forming a foveal image of F will happen sooner than in the previous example (that is for a lesser rotation angle).

Since the fovea is slightly temporal, the formation of a foveal image occurs for a lesser angle of rotation (counter clock wise in this example)
The fact that an (inverted) image of the fixation point is formed on the fovea means that in an eye free of optical aberrations, all the light rays emitted by F and collected by the pupil are converging and intersecting on the fovea.
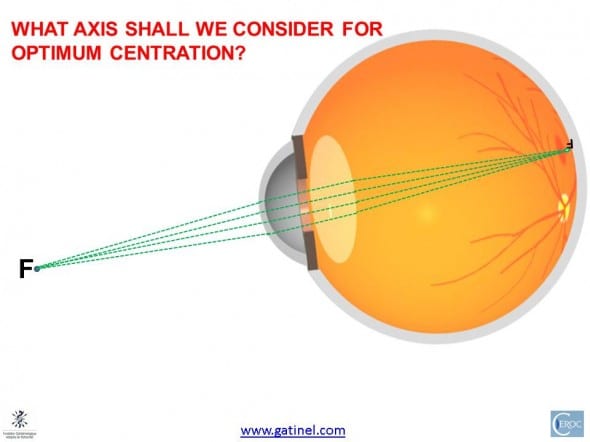
The formation of the foveal image is caused by the focalization of light rays emitted by the source and admitted by the eye’s netrance pupil. This is not fully informative on where to locate an « optimal » refractive concentric central subzone
This is however not yet informative with regards to the optimal centering location. One may claim that since the bundle of ray which is collected by the pupil is centered by a ray (the « chief ray), and since by definition this ray is going through the center of the pupil, this should coincide with an optimal center for refractive procedure. Unfortunately, this may not hold true for all corneal based refractive surgical procedures, especially those in which the functional optical zone is narrow (hyperopic photoablations, corneal inlays). Additionally, it should be kept in mind that at the time of surgery, the eye to be operated presents (by nature) a refractive error (ametropia: myopia, hyperopia, etc.) : as opposed to on the previous diagram, the rays may converge before (or after) the retina, leading to a defocused retinal image. In addition, the center of the pupil is a moving target, as it has been shown that it can shift up to 400 microns from constricted to dilated diameters.
Visual axis
What is the visual axis? It should not be confounded with the optical (« best fit ») axis. Once the image of the fixation point F is formed on the fovea, one may conceptualize that there is one « ray » of light that joins the fixation target to the fovea. Rays of light are convenient concepts to predict some of the behavior of light, but they are just concepts: light is a strange phenomena made of particles (photons) which exhibits « wave » properties. Rays of light are somewhat the simplified » materialization » of the path of photons. Given the absence of common optical axis between the corneal and the crystalline lens, there may not be any significant number of photons that would travel in an exact straight line from the fixation point (F) to the fovea. However, one may define an axis along which the angular deviation along the photon’s path is minimum. This axis could correspond to a broken line, represented by a first segment equal to the incident ray, and a second segment corresponding to the refracted ray. What would be the corresponding incident and refracted rays?
Taking the « best fit » optical axis as reference, the angle of such incident ray (from source to cornea) formed with this optical axis is equal to the angle of the refracted ray (from back crystalline lens surface to fovea) with this same optical axis.
The cornea and the lens form a « thick lens dual system », that can be simplified owing to paraxial theory by defining its cardinal points (foci, principal points, and nodal points). Optical scientists define two nodal points for the eye, but their proximity allows some simplification and we will assume that there is only one nodal point, which is located slightly behind the crystalline lens posterior capsule. The location of each of the nodal points is wavelength dependant, but the variation caused by shifting the wavelength from blue to red extremes of the visual color spectrum results in negligible changes. Traveling along the nodal ray from the point source, a photon would not undergo any angular deviation until it impinges on the fovea. This trajectory corresponds to the idealized visual axis, as it also controls for the axis that minimizes transverse polychromatic aberration.
The ray joining the fixation point to the fovea is called the nodal ray, owing to the existence of a unique nodal point. This simplification allows to define as a point through which each of the incident ray is refracted with the same angle than the angle of incidence; this ray undergoes « no deviation ». This trajectory defines our idealized visual axis, for reasons that will be explained later.
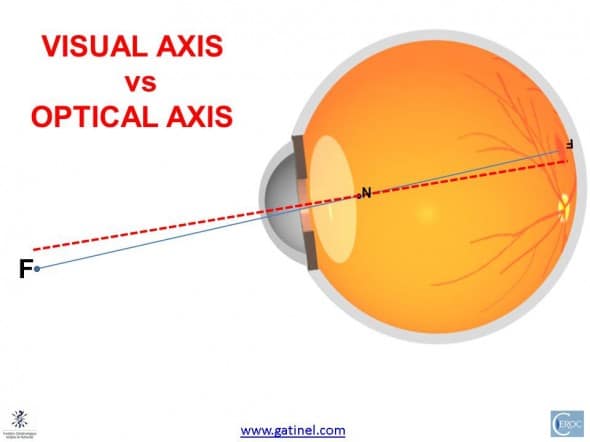
The visual axis is defined by the (solid) line joining the fixation point to the 1st nodal point, and the 2nd nodal point to the fovea. Given the proximity of the nodal points, one can simplify this concept by keeping the posterior nodal point as a unique nodal point. The angle between the visual axis (broken line) and the optical axis is about 5° on average.
The optical axis should not be confounded with the pupillary axis. The pupillary axis is used to reference several angles such as angle kappa: angle kappa is the angle that is formed by the pupillary axis and the visual axis.
Visual axis and polychromatic aberrations
When photons of different wave light (red, blue, etc.) undergo refractions (going from a media to another), the angle of refraction that they take depends from their wavelength (blue photons tend to be refracted with a larger angle than green photons, and green photons tend themselves to bend more than red photons). If a white source emits these different wavelengths, then the photons of different wavelengths will not be refracted to the same location on the image plane (retina, screen, CCD, etc.). This is called « chromatic aberration ». Ophthalmologists use this property when they test the refraction of their patient, by showing them letters in red and green. The photo objectives of reflex cameras are made of several lenses partly to correct for chromatic aberrations (they are also selected and designed to minimize « monochromatic » aberrations). Chromatic aberrations can be divided into two sub-categories: longitudinal chromatic aberration (LCA) and transverse chromatic aberration (TCA). Transverse chromatic aberration increases when polychromatic light is refracted away from the direction containing the nodal points. Conversely, transverse chromatic aberration is null if the aperture stop (the iris pupil in the case of the eye) is centered on the line joining the fixation point source to the nodal point : since there is no change in the direction of a photon traveling along this path (it keeps the same « angle ») , the path to the nodal point and to the fovea would be that of any photon emitted along this direction, regardless of its wavelength. Hence, this results in the minimization of transverse chromatic aberration, and satisfies the the goal of maximizing the optical quality of the retinal image. Even if human eyes (and/or the visual system) seem to be robust to perceived chromatic aberration, its minimization still warrants the optimization of the photon capture rate at the foveal plane, regardless of their energy (wavelength).
This line from the fixation point, to the nodal point and then to fovea where it meets with the cones packed with the highest density and which alignment is optimized to that same line defines what is called the « visual axis ». The problem is that this axis and its intercept at the corneal plane are difficult to identify using simple clinical methods. From the geometry of the eye in cross section (see figure), we can anticipate a slightly nasal deviation with regards to the center of the cornea (and the entrance pupil).
Locating the ocular axes
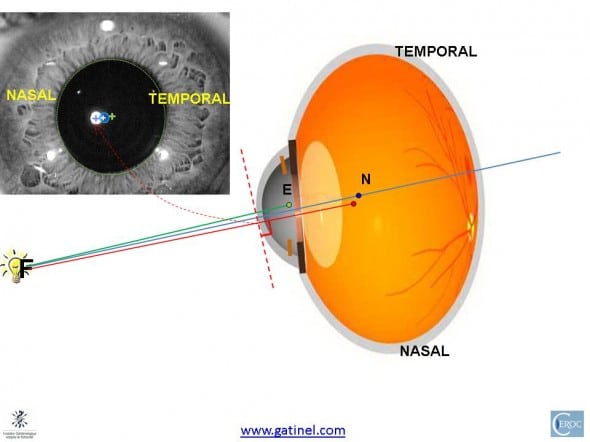
The following illustration shows the different axes relations in an average eye :
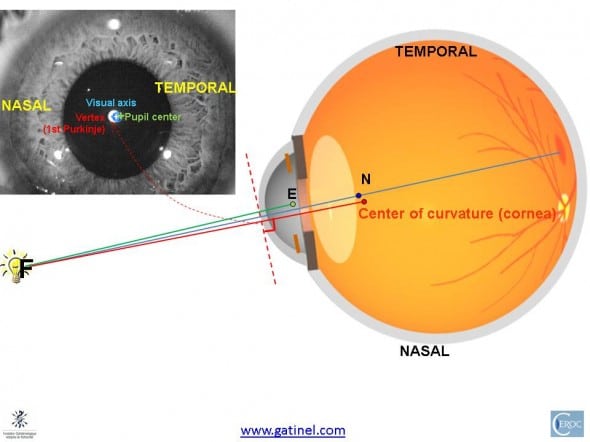
On average, the visual axis intercept of the visual axis may be located nasally to the intercept of the line of sight with the cornea (this point is called the « corneal sighting center » in the optometry litterature). Hence, it tends to be close to the vertex normal (bright spot which is the reflexion of the fixation source on the cornea). The vertex is aligned with the center of curvature of the cornea. E is the center of the entrance pupil. N is the posterior nodal point.
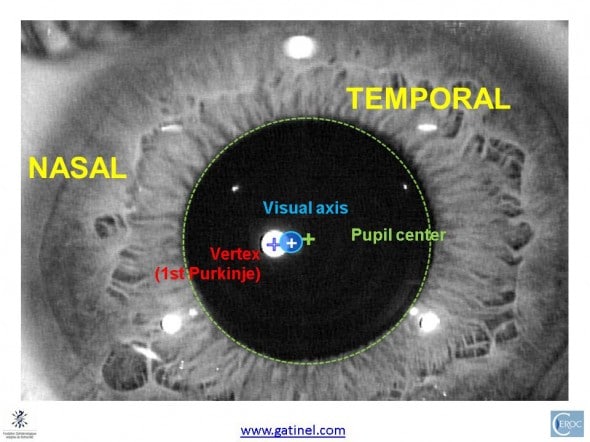
A magnified view of the pupil may allow to predict where the intercepts with the corneal dome of these principal axes are located.
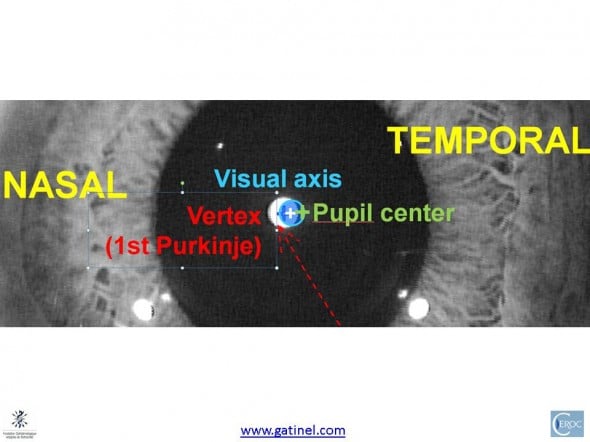
The probable intercept of the visual axis with the cornea is supposedly slightly nasal to the pupil center, and close to the corneal vertex.
Of course, these locations have been shown a bit arbitrarily; there may also be slight vertical displacements of this points, which have no reason to lie on the same horizontal line. Also, remember that these concepts are a bit idealistic, as there may not be one « straight » line visual axis in non-rotationally symetrical eyes. However, these simplifications are useful to better apprehend this problem.
Given these assumptions, centering on the corneal vertex may be a reasonable way of minimizing transverse chromatic aberration in procedures that incur a narrowing of the functional zone (ex: KAMRA inlay).
In some eyes, these axes may show more separation. Often, in hyperopic or highly astigmatic eyes, the nasal shift of the vertex normal is more pronounced. This is the consequence of a larger angle Kappa, which can be attributed at least partly (in a deterministic approach) to the fact that the axial length is reduced, but the distance between the best fit optical axis and the fovea preserved. Hence, the external rotation of the globe has to be slightly increased compared to a longer eye in order to gaze at the target.
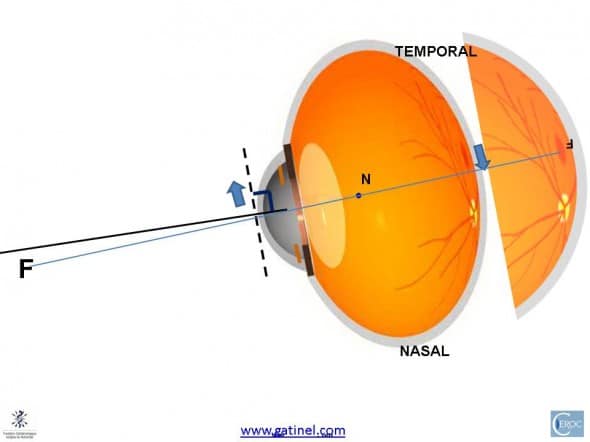
In a shorter eye, the distance from the optic nerve to the fovea may be constant: the geometry of the figure show that the reduction in axial length causes the fovea to be proportionally ( rotationally) more temporal than in the case of a longer eye. To align with the same target, the shorter eye has to rotate externally. On the figure, the pupil axis is shown in black, relative to longer eye the visual axis (in blue).
Having reached foveal fixation, the orientation of the shorter eye makes the kappa angle larger:
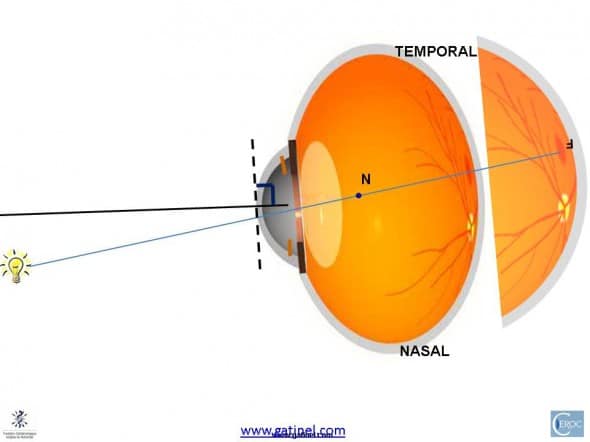
To fixate the target, the shorter eye has to rotate more externally. This causes an increase in the Kappa angle.
Let us now represent in cross section the line of sight, visual axis and normal vertex respective locations in an eye with larger angle Kappa :
Due to the increased outer rotation of the globe (resulting in a larger kappa angle, not shown here); the separation between the intercepts of the different remarkable axes is increased.
A magnified view of the pupil area allows to better visualize the predicted locations of the different axes.
In an eye with a larger kappa angle, the vertex normal appears to be more nasally located. The position of the visual axis may be slightly temporal to the vertex normal.
This justifies the following recommendation: in eyes with large apparent angle Kappa, the best location for centering a corneal based refractive procedure is to use a spot located between the vertex normal and the center of the entrance pupil (ex: choosing the point located midway, or 2/3 from pupil center – 1/3 from vertex). Again, the exact location of the visual axis remains speculative, but this strategy minimizes the risk of increasing transerve chromatic aberration, optimizes the efficiency of admitted photons to meet with foveal cones, and prevents from significantly degrading the quality of the retinal image.
Those concepts can also be applied for intraocular lens IOL centration. However, in this situation, the control of centration of the IOL may not be as efficient as for corneal surgery, since IOLs tend to « auto center » in the capsular bag at the time of the surgery.


No, since the entrance pupil is not even centered on the limbus in the vast majority of human eyes!
Dear,
Should we ever center on to the limbus?
Thanks for your kind comment. The line starting form E (center of the entrance pupil), and which connects with the fixation target is the line of sight. The line in red is the keratometric axis, which indicates the vertex apparent location at the corneal plane (first Purkinje image). The line starting from the nodal points is the the visual axis, which forms with the pupillary axis (not shown) the Kappa angle.
Dr Gatinel , hats off to you for sparing time and effort to explain such a complex issue. I had to read it four times to get a grasp of what you were saying. I have however one doubt. In the second last diagram showing cross section with various axes I have presumed that the axis starting from E is pupillary axis and the one passing through N is visual axis. So the axis in red should be the line of sight as it indicates the vertex which is nasal to other points. Then why does the line of sight start from behind the lens when it should start from the centre of the entrance pupil ?
Grazie! Molto chiaro e istruttivo