Calcul d’implant – formule théorique
Le calcul de la puissance optique de l’implant posé pour remplacer le cristallin est un temps important en chirurgie de la cataracte. Dans le cas de la chirurgie pour cataracte, on retire le cristallin car celui-ci présente une opacification responsable d’une gêne visuelle (perte d’acuité visuelle – dixièmes, éblouissements, voile, etc.). Dans le cas de la chirurgie du cristallin clair, on retire le cristallin non opacifié dans le cadre d’une procédure à visée réfractive : on le remplace par un implant dont la puissance optique (vergence) est calculée pour corriger une erreur réfractive sévère (amétropie prononcée: myopie forte, hypermétropie forte, astigmatisme élevé).
La puissance optique de l’implant (vergence) est exprimée en dioptries (symbole : D) : elle permet à l’ optique de l’implant de faire converger la lumière vers la rétine. Elle est calculée pour un implant placé dans un milieu aqueux (humeur aqueuse à l’avant de l’implant, et vitré à l’arrière), qui est muni d’un indice de réfraction proche de 1,33 (on choisit généralement la valeur n=1,336 pour le milieu dans lequel baigne l’implant).
Cette page expose les principes généraux du calcul de la puissance de l’implant posé au cours de la chirurgie de la cataracte. L’utilisation du calcul des vergences de la cornée et du cristallin artificiel permet d’établir une formule théorique de base, qui est encore utilisée aujourd’hui dans les formules de dernières génération. Les éléments qui interviennent dans ce calcul sont logiquement la puissance de la cornée, la longueur de l’oeil (longueur axiale), et la position effective de l’implant dans l’oeil. Si les deux premiers paramètres sont mesurables avant la chirurgie, le troisième ne peut qu’être prédit. C’est dans la manière dont les formules « prédisent » la position finale de l’implant dans l’oeil que résident leurs principales différences.
Voire pour plus d’informations (en anglais): IOL power formula
Quelle que soit l’indication du retrait du cristallin, le choix adéquat de la puissance de l’implant destiné à le remplacer conditionne le résultat réfractif, c’est-à-dire la capacité à corriger le défaut optique éventuel qui existait avant l’intervention (myopie, hypermétropie etc.) ou à maintenir l’absence de défaut optique (emmétropie).
Pour obtenir le résultat réfractif souhaité, il faut effectuer un calcul préopératoire appelé biométrie. Celui-ci repose sur la prise en compte de certaines mesures oculaires, et de leur utilisation dans une formule de calcul. On distingue deux types de formules : les formules statistiques, et les formules « exactes », qui font appel à un calcul optique.
Cette page est consacrée à l’établissement d’une formule exacte simple, reposant sur le calcul optique et faisant appel à la formule de vergence, dont le calcul de la puissance de l’implant est une application directe et importante.
Données du problème
L’œil opéré de cataracte avec implant peut être modélisé comme un système optique simple, muni de deux lentilles : la cornée, et l’implant.
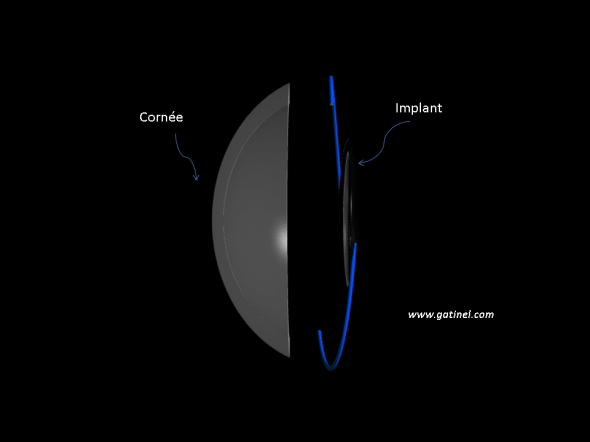
Le couple « cornée et implant » doit posséder une puissance réfractive à même de faire focaliser la lumière incidente émise par une source lointaine vers la rétine. On néglige l’épaisseur du cristallin et de l’implant : ils sont considérés comme des lentilles minces.
Le but de notre calcul est d’établir une formule qui fournit la puissance de l’implant permettant à l’œil d’être emmétrope, c’est-à-dire bénéficiant d’une vision nette de loin sans qu’il soit besoin de l’équiper en lunettes ou verres de contact.
Pour obtenir une vision claire de loin, il faut que la puissance optique de la cornée ET celle de l’implant de cristallin artificiel permettent aux rayons lumineux incidents émis par une source lointaine d’être focalisés sur la rétine.
La chirurgie de la cataracte ne modifie pas significativement la puissance optique de la cornée ; la vergence de la cornée peut être mesurée en préopératoire. La longueur axiale de l’œil, qui est la distance comprise entre la cornée et la rétine est également inchangée après la chirurgie.
Le retrait du cristallin « réduit » la vergence de l’œil : la lumière est focalisée en arrière de la rétine par la cornée seule ; l’oeil devient hypermétrope. L’ajout de l’implant doit permettre d’augmenter la vergence de l’oeil afin de « ramener » le plan focal du couple cornée + implant dans le plan de la rétine.
Pour l’œil opéré, la puissance (vergence) du couple « cornée + implant » dépend de trois facteurs :
– la puissance de la cornée
– la puissance intrinsèque de l’implant (ce que notre formule cherche à calculer)
– la position de l’implant vis-à-vis de la cornée, appelée position effective de l’implant (effective lens position) : il existe une incertitude vis-à-vis de la position exacte de l’implant, et ce point est important.
Rappels :
Pour un objet source situé à l’extérieur de l’œil, la cornée et l’implant peuvent être assimilés de manière simplifiée à un couple de lentilles convergentes. Dans ce qui suit, on considère que ces lentilles sont minces. La puissance optique (ou vergence) d’une lentille s’exprime comme l’inverse de sa distance focale : D=1/F (F doit être exprimé en mètre, D est en dioptries)
La formule de vergence permet de prédire la position de l’image formée par une lentille d’un objet source :
Vi = Vo + D ou Vi est la vergence de l’image, Vo la vergence de l’objet et D la puissance de la lentille : ces grandeurs sont exprimées en unité « dioptrie ». Vo est égal à l’inverse de la distance de l’objet (notée D0) vis-à-vis de la lentille (en mètre, avec un signe négatif par convention si cette distance est dirigée vers la gauche) et Vi est égal à l’inverse de la distance de l’image (notée Di, exprimée en mètres avec un signe positif si cette distance est dirigée vers la droite).
Application de la formule de vergence au couple cornée + implant.
Pour un objet source, l’image formée dépend de deux réfractions successives : celle de la cornée, puis celle de l’implant.
Voir ici pour une séquence plus détaillée (en anglais)
Réfraction par la cornée :
On peut l’exprimer comme :
Vi = Vo + K
La puissance optique de la cornée est K, et est mesurée avant l’intervention (kératométrie).
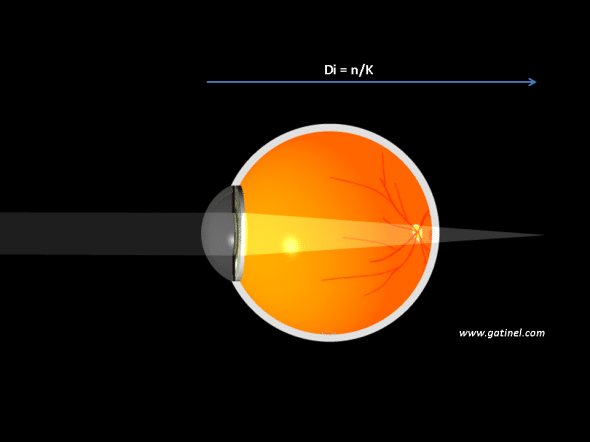
Pour un objet situé à l’infini, la vergence Vo est nulle (D0 est infini). La vergence Vi est égale à n/Di où n est l’indice de réfraction du vitré.
Di peut donc être calculée : c’est le plan de l’image formée par la cornée : cette image devient l’objet pour la réfraction par l’implant
Réfraction par l’implant
La figure suivante renseigne sur la position de l’image vis-à-vis de l’implant.
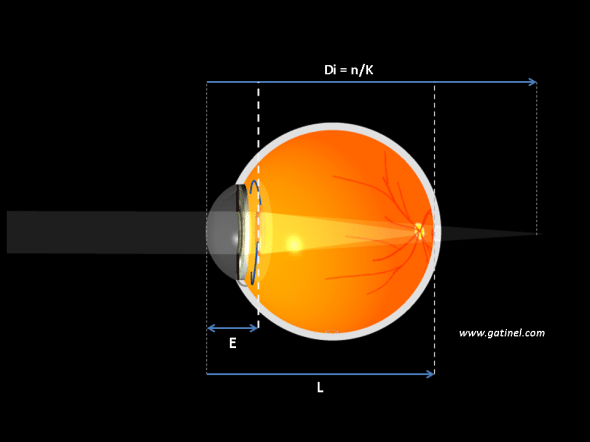
La distance entre implant et cornée est notée E. Cette distance est appelée « position effective de l’implant » (effective lens position). Elle est prédite, car elle ne peut être mesurée en préopératoire: l’implant peut se positionner différemment d’un oeil à l’autre, en fonction de certains paramètres anatomiques (profondeur de la chambre antérieure de l’oeil, anatomie de l’espace en arrière de l’iris appelé sulcus, état de l’humeur vitrée, etc.)
La distance de l’implant vis-à-vis de la cornée est notée E. Sur le schéma, on observe que la distance entre la première image (formée par la cornée) et l’implant est égale à Di – E.
La vergence de cette première image est égale à n/(Di – E)
Pour que l’œil voie net en vision de loin, l’implant doit focaliser les rayons issus de la première image dans le plan de la rétine. On appelle L la longueur axiale de l’œil, la distance entre l’implant et la rétine est égale à L-E.
On connait la position du foyer vers lequel converge la lumière après réfraction par la cornée seule (oeil aphake). On peut appliquer la formule de vergence à partir de ce point focal, qui sert d’objet pour l’implant. La vergence de l’image rétinienne correspond à la distance (L-E).
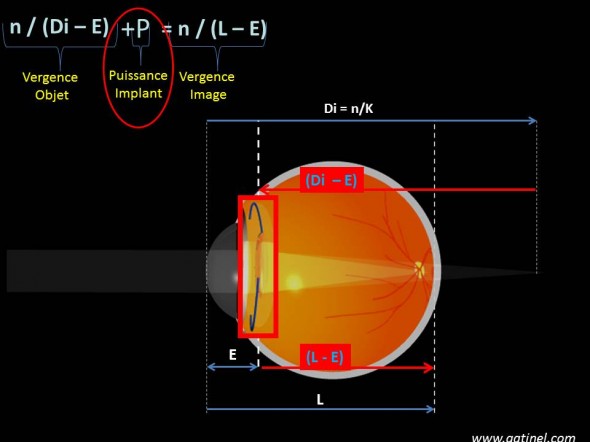
La formule de vergence peut être appliquée à l’implant, dont l’objet est l’image formée par la cornée, et l’image doit se former dans le plan rétinien.
On peut écrire la formule de vergence comme suit :
n / (Di – E) + P = n / (L – E) où P est la puissance de l’implant qui donne à l’œil l’emmétropie.
On obtient ainsi la formule :
P = n/ (L – E) – n / (Di – E)
On remplace Di par n/K (puisque K = n/Di)
P = n / (L – E) – n /( (n/K) – E)
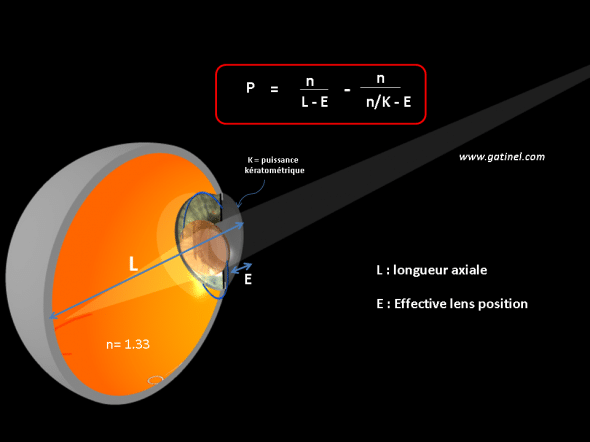
La formule théorique exprime la puissance (vergence) de l’implant en fonction de la longueur axiale de l’oeil, la kératométrie et la position effective de l’implant dans l’oeil.
Si la kératométrie est mesurée à 43 D, la longueur axiale à 23.3mm, et que la position effective de l’implant est estimée à 5mm, on obtient P =21.5 D (avec n = 1.33). Il est fondamental d’observer que dans cette formule, E est la seule variable que l’on ne peut pas mesurer en préopératoire, puisque cette grandeur correspond à la position finale de l’implant dans l’œil, et que celle-ci n’est pas égale,ni anatomiquement (l’implant est beaucoup plus fin) ni optiquement à celle du cristallin. On ne peut pas simplement remplacer E par la profondeur préopératoire de la chambre antérieure mesurée en pré opératoire, car le retrait du volume occupé par le cortex et le noyau du cristallin, le comportement de l’implant dans le segment postérieur sont autant de variables à même de faire varier la position finale de l’implant.
Ainsi, cette formule est la « mère » de toutes les formules modernes de calcul d’implant. Elle permet de calculer la puissance à donner à l’implant pour corriger l’œil opéré de cataracte pour la vision de loin. Elle néglige un certain nombre de facteurs et utilise certaines simplifications (la cornée et l’implant sont considérés comme des lentilles minces). Les formules théoriques de différentes génération diffèrent surtout dans la manière dont elles cherchent à anticiper au mieux la valeur de la position effective de l’implant. Cette position sera prédite d’autant plus loin de la cornée que l’oeil est long, et que la cornée est cambrée, avec les formules qui utilisent ces variables dans le calcul prédictif.
Pour les calculs de distances « optiques » séparant les éléments (cornée / implant) assimilés à des lentilles épaisses et à partir des positions anatomiques, il faut leur substituer leurs équivalents simplifiés à partir des points cardinaux (plans principaux). Ce sont ces plans (voir plans principaux et optique paraxiale) qui servent de référence pour le calcul optique paraxial. (en anglais: principal planes)
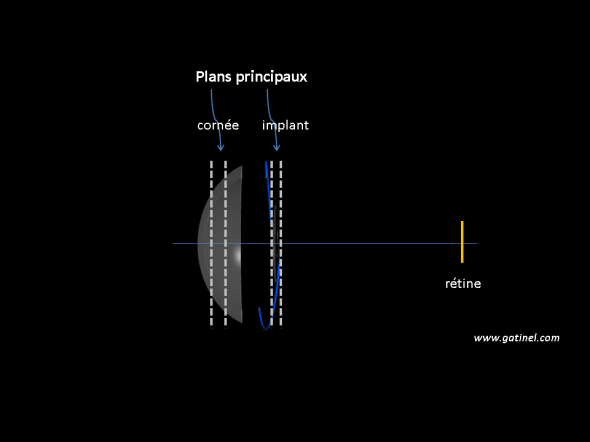
Un modèle d’œil simplifié paraxial suppose que les position des structures réfractives (cornée et implant) soient représentées par leur plans principaux. La position des plans dépend de la courbure des surfaces impliquées, de leur épaisseur et des indices de réfraction des différents milieux considérés. Les plans principaux de la cornée sont en pratique quasiment confondus et situés en avant de celle-ci, à ue distance d’environ 0.060 mm de la surface cornéenne)

C’est une question dont la réponse fait appel à des points un peu techniques. Les formules doivent prendre en compte le fait que la cornée a été opérée au niveau de sa face antérieure (PKR) et que de ce fait, la prédiction de la position de l’implant ne doit pas faire appel à ce paramètre. Il est également recommandé d’utiliser un topographe cornéen et un mode de calcul spécifique pour bien estimer la puissance de la cornée. Les formules de dernières génération possèdent une option pour les cornées opérées. Cette option active ou désactive certains paramètres d’importance pour assurer un calcul le plus précis possible. Nous avons mis au point une formule de calcul d’implant (PEARL-DGS) qui comporte une option pour les yeux « complexes »: https://iolsolver.com/main
Bonjour docteur.svp comment calculer la puissance de IOL chez un patient opérer déjà pour PKR où bien c’est la même formule chez un sujet normal ?merci
Très bonne question posée par bonnefoix thierry.
Dommage que nous n’ayons pas de réponse.
Bonjour,
quels sont les résultats réfractifs et leur prévision pour les personnes, au départ soit myopes, soit hypermétropes et qui ont subi une chirurgie réfractive cornéenne ? Le calcul de l’implant est t-il plus difficile, les résultats plus aléatoires ? Et qu’en est-il de l’astigmatisme préopératoire ? Enfin, une retouche lasik ou PKR est-elle possible après l’opération ?
Merci pour votre message; les formules de vergences « simplifiées » s’appliquent à des surfaces assimilables à des dioptres sphériques. Il faut distinguer la puissance d’un dioptre (qui dépend de la différence entre son indice et celui du milieu incident), et les formules de vergences proprement dites qui découlent d’une simplification paraxiale. La cornée est généralement assimilée à un dioptre sphérique dont la puissance est égale à l’inverse de son rayon de courbure multiplié par la différence d’indice (air vs indice kératométrique). L’indice kératométrique possède une valeur « fictive » destinée à minorer le résultat de ce calcul vis à vis de celui qui utiliserait une valeur d’indice de réfraction « réellle » (l’indice du stroma cornéen est égal à 1.376, l’indice de réfraction « kératométrique » de la cornée est plutôt proche de 1.33). Ceci afin d' »anticiper » l’effet de la face postérieure de la cornée. Les formules biométriques plus complexes prennent en compte les surfaces antérieures et postérieures de la cornée (à condition que les mesures de celles-ci soient disponibles), et considèrent aussi l’implant comme une « lentille épaisse ».
En théorie, cela est possible, surtout si l’implant est décentré. Le tilt isolé est également pourvoyeur d’astigmatisme. Un examen aberrométrique devrait par ailleurs révéler la présence d’aberrations de haut degré comme le coma, le trefoil, l’astigmatisme de haut degré, etc.
bonjour docteur , je suis chirurgien ophtalmologue, j aimerai savoir est ce que un implat incliné(un haptique dans le sac capsulaire et l autre haptique dans le sulcus cillaire ) peut entrainer un astigmatisme ou tout autre consequence ?
MERCI POUR VOTRE DISPONIBILITE.
Bonjour,
je ne peux que commencer par des félicitations pour ce site, qui est une véritable mine d’or d’information sur les sujets traités, alliant un parfait dosage entre concision et précision.
Ma question concerne la base théorique:
– vous faites un rappel très utile sur la formule de vergence: Vi = Vo + D qui permet de calculer la vergence de l’image d’une lentille, qui transposée à la cornée peut s’écrire sous la forme:
Vi= Vo + K.
– Dans la cas de la biométrie, nous cherchons, à cette étape, à calculer Di de la cornée.
– K se mesure, Vo = O pour un objet situé à l’infini, du coup Vi= K.
– si V= 1/D, alors Vi= 1/Di et du coup Di= 1/K dans mon raisonnement…
…qui manifestement est faux car vous écrivez que Di= n/K. A quel moment, n (indice du corps vitré) rentre en ligne de compte?
Ou alors la formule V= 1/D n’est valable que pour des milieux d’indices de réfraction équivalents de part et d’autre du système optique?
La cornée d’ailleurs est à considérer comme un dioptre sphérique (vu que la kératométrie ne se soucie pas de la pachymétrie et de face postérieure) ou comme une lentille convexe, dans ce cas là?
Je vous remercie par avance pour votre réponse.
Il n’y a aucune obligation de résultat en matière de résultat réfractif suite à une chirurgie de la cataracte qui s’est bien déroulée et pour laquelle l’implant dont la puissance qui a été prédite par la biométrie preopératoire pour atteindre le résultat souhaité (chez vous voir net de loin sans lunettes) a été posé. Le calcul d’implant est une pure prédiction, car nul ne peut savoir exactement à quelle distance de la cornée l’implant se positionnera au décours de l’intervention. Heureusement, cette incertitude a généralement de faibles conséquences en matière d’écart avec la correction prédite. Mais dans certaines configurations (yeoux très myopes ou hypermétropes, géométrie oculaire particulière, etc.) l’écart peut être significatif (ex: myopie, ou hypérmétropie jusqu’à 2 D environ). Par ailleurs, l’objectif initial d’une chirurgie de la cataracte est de rétablir la transparence des milieux oculaires: le choix d’un implant de puissance adaptée au souhait réfractif du patient est bien entendu une option légitime, mais cet aspect réfractif doit être considéré comme un « bonus ». La chirurgie réfractive au laser peut tout à fait corriger un défaut optique qui n’était pas prédit avant la chirurgie de la cataracte; il est dans ce cas à la charge entière du patient, et cet acte ne fait pas l’objet d’une prise en charge par la SS en France.
Bonjour. J’ai été opérée de la cataracte il y a 1 an. J’avais choisi la vision de loin et port de lunettes de près. Un choix bien exprimé auprès de mon chirurgien. Mais au bout d’un an de vue un peu moins nette de l’oeil droit, celui ci me dit que l’implant s’est mal positionné et me propose du laser (lazic) pour 1 coût de 1300€. Est ce à moi de payer ce soucis ? Suis je responsable? N’a t’il pas un devoir de réussite ? Que dois je faire ? Vers qui me tourner? .merci de votreHery danielle reponse
Bonjour Monsieur,
J’ai lu avec intérêt l’article sur les dysphotopsies, je vous en remercie. Opérée de la cataracte en avril 2018, je ressens toujours, même j’ai l’impression davantage, la gêne de cette lumière circulaire parasite dans certaines conditions. Ma question serait : que puis-je faire et la rétine peut-elle être affectée (ou l’oeil en général) par ce phénomène ?
Merci de la réponse que vous avez bien voulu me donner déjà et excusez-moi si mon nouveau message vous est déjà parvenu. (Je le recommence car je crois l’avoir mal envoyé).
Les symptômes que vous présentez évoquent fortement la présence de ce que l’on appelle des dysphotopsies: https://www.gatinel.com/chirurgie-de-la-cataracte/dysphotopsies/
Est-ce que vous pourriez me dire pourquoi depuis mon opération de la cataracte je vois, très souvent, un cercle très régulier de lumière par exemple si une source de lumière est perpendiculaire à mon oeil opéré ou autour d’une source de lumière isolée dans l’obscurité comme un simple point lumineux ou une lumière type réveil matin dans le noir. C’est comme si je voyais les bords de l’implant ! C’est assez désagréable bien que ma vue à l’infini soit parfaitement corrigée.
Cordialement.
La mesure de la longueur axiale en interférométrie (OCT, biométrie optique) n’est pas significativement altérée par la cataracte et la vergence du cristallin (même en cas de myopie d’indice). Il n’y a donc pas de risque de surcorrection de la myopie par une mésestimation de la longueur axiale.
Bonjour,
La mesure de la distance L (géométrie réelle de l’oeil en profondeur) est-elle précise ? Le principe de l’instrument utilisé pour la mesurer s’affranchit-il de la vergence réelle du cristallin à remplacer , et qui a varié récemment dans mon cas par un effet secondaire de la cataracte ?
En effet, j’ai compris que l’excédent récent de ma myopie (2 dioptries !) était lié à la cataracte et non à la forme de mon oeil , restée stable sur 40 ans si j’en crois l’historique de mes ordonnances ophtalmologiques avant le début de ma cataracte il y a 2 ans.
Autrement dit, si la mesure de la distance L est affectée par la vergence actuelle de mon cristallin avec sa cataracte, j’ai peur d’avoir une myopie sur-corrigée par l’opération . Peut-être serait-il alors préférable de calculer L à partir des éléments réels de ma myopie avant l’apparition de la cataracte ?
Merci de vos éclaircissements sur le principe de la mesure de L et de sa dépendance ou non de la vergence du cristallin à remplacer.
Cordialement.
Le calcul de la vergence globale fait appel à une formule de vergence qui ne considère pas le trajet réel des rayons: cette formule de vergence découle de certaines simplifications faites en optique paraxiale. Le calcul du trajet des rayons (ray tracing) est une approche différente, pour laquelle l’incidence convergente des rayons sur l’implant est bien entendu considérée.
Bonjour,
lors du calcule de la vergence globale, considérez vous que les rayons ayant traversés la cornée sont tous parallèles avant de venir traverser l’implant (rayon venant de l’infini convergeant au foyer de l’implant)?
Merci
Il faut effectivement faire un choix, en sachant qu’une légère différence de correction entre les deux yeux (si les deux sont à opérer) peut permettre de réduire la dépendance au lunettes; par exemple, opérer un oeil pour voir net de loin, et laisser une légère myopie sur l’autre pour facilité la vision de près. Il faut avant tout que vous sachiez dans quelles circonstances vous accepterez le plus de devoir porter des lunettes et faire un choix en conséquence.
je dois me faire opérer de la cataracte mais le chirurgien ne peut pas me poser un implant multifocal, je dois donc choisir entre correction de loin ou de près et ce n’est pas facile de prendre une décision. si correction de loin il va falloir sans arrêt mettre les lunettes pour lire ds les magasins les étiquettes prix etc; si correction de près idem pour se diriger
comment choisir au mieux pour se faciliter la vie?
merci de me conseiller pour une situation future rationnelle