Novel Polynomial Decomposition: Clinical Examples
CLINICAL EXAMPLES: TAKING OUR THEORY TO YOUR CLINICAL PRACTICE!
To aid understanding of the application of a novel wavefront decomposition method and polynomials (+read the JOSA A paper), we have created further clinical examples including clinical scenarios you will come across in your practice.

Conversion Zernike to LD HD (Low Degre / High Degree): proper analytical methods can be implemented to convert a Zernike coefficient expansion into a new LD-HD coefficient expansion.
Current wavefront sensors (read more about wavefront sensing) express the wavefront as a sum of Zernike weighted coefficients (read more about Zernike polynomials). From these, one can calculate the values of the GM coefficients in the new basis called « LD-HD » for Low Degree / High Degree. Such calculation requires the rearrangement or reorganization within and between the low vs high degree terms which are parceled or combined in the high order modes.
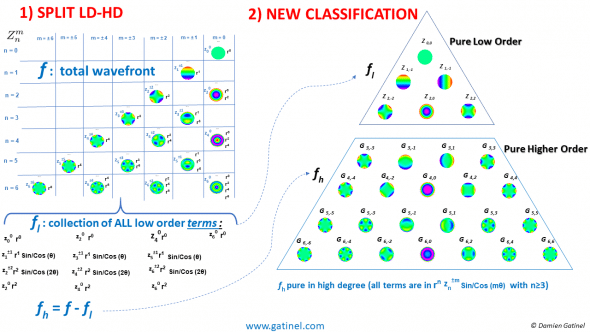
fl (for f low) is obtained after collecting all the low order terms (those present in the low order modes, and those which contaminate the HO modes. Subtracting fl to the total wavefront f enables to obtain the « pure » HO WF component (fh). This pure HO component, called fh, is decomposed using the new series of orthogonal modes.
The new series of orthogonal higher order modes do NOT contain low order terms. Hence, that new decomposition method does not induce undesirable interactions between the high and low order modes’ coefficients (no artefactual tilt or defocus coefficients are induced).
Such calculations have been implemented in a beta-software running on the OPD-scan III wavefront sensor, which has been used extensively to provide the following examples’ data (special thanks to the RnD department of the Nidek company).
EXAMPLE 1
Orthokeratology (ortho-k) is the fitting of specially designed gas permeable contact lenses that are worn overnight. This 25 y.o patient has her myopia (-2.50 D) corrected by ortho-K.
The eye is emmetropic in photopic conditions (20/15 uncorrected visual acuity) but perceives large halos in mesopic conditions.

The vergence map displays the local dioptric power variations throughout the pupil area (for mesopic conditions).
In the central area, there are negligible to slight hyperopic errors (about 0.50D). In the extreme periphery, there is a rapid increase in the local vergence and marked myopic change. This ring of peripheral myopia is the consequence of the increase in positive spherical aberration. It explains the perception of halos in mesopic conditions. Note that the predicted PSF from positive Zernike spherical aberration presents concentric rings, whereas the perception of the patient when viewing a bright light source is a continuous halos.
The following figure displays the Zernike vs New LD/HD wavefront coefficients:
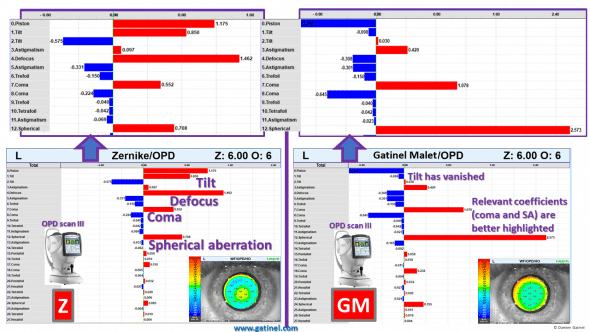
The wavefront decomposition using the Zernike polynomials is shown on the left (6 mm pupil): the inspection of the modes’ coefficients suggests that tilt and defocus are the most relevant aberrations, despite significant coma and spherical aberration being elevated.
The wavefront decomposition using the LD/HD method reveals that tilt and defocus have almost completely vanished as there is no need of compensating the low order terms embedded in the high order modes in the lower order wavefront component. There is also no artificial reduction of the spherical aberration and coma coefficients.
A vectorial depiction of the wavefront decomposition between the Zernike vs LD-HD methods is shown:
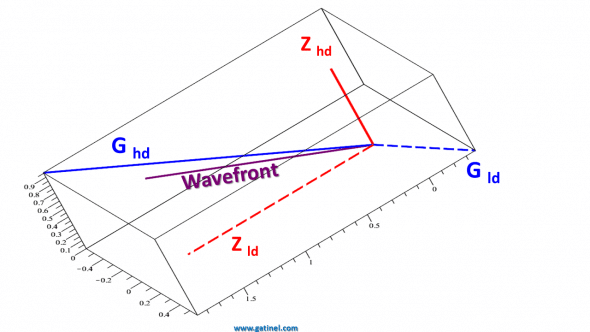
Vectorial depiction of total Wavefront decomposition : Zld : sum of Zernike low order, Zhd: sum of Zernike high order, Gld: sum of Gatinel-Malet low order, Ghd: sum of Gatinel-Malet high order. The Zernike reconstruction tends to underestimate the role of the high order within the total wavefront error.
In this representation, the low and higher order wavefront components are orthogonal in the Zernike decomposition method, but not in the LD-HD decomposition method. This is not detrimental to the clinical interpretation of the case. On the contrary, this non-orthogonality better reflects the relative independence and differences between low and higher-order wavefront error components.
The comparison between the refraction and retinal image predicted by the two wavefront methods for the best spectacle correction is shown here:
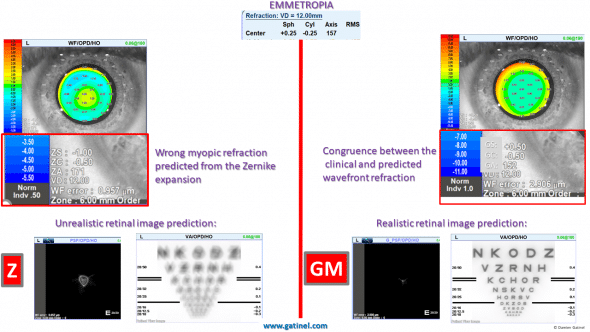
The comparison between the refraction and retinal image predicted by the two wavefront methods (Z: Zernike, GM: Gatinel Malet)
There is no correspondence between the clinical refraction (emmetropia) and the Zernike predicted refraction (-1.25D of spherical equivalent). Conversely, the refraction predicted by the new wavefront reconstruction method (LD-HD) correlates with the clinical refraction.
The retinal image prediction for the high order wavefront component of the Zernike based wavefront reconstruction is unrealistic as it predicts a dramatic reduction in visual acuity (see the retinal image simulation of the perception of the visual acuity chart). This is because of the presence of the defocus term in the Zernike spherical aberration component. The LD-HD wavefront reconstruction provides a more realistic output (reduction of the contrast with no reduction of the maximal contrast visual acuity).
EXAMPLE 2:
This 26 y.o male complains about mild halos at night, which appeared after his LASIK procedure which corrected for -5D of myopia.
The right eye is emmetropic (20/15 uncorrected visual acuity).
The Zernike predicted refraction is biased by the defocus coefficients which correspond to artefactual compensation for low order terms embedded in the Z40 mode:
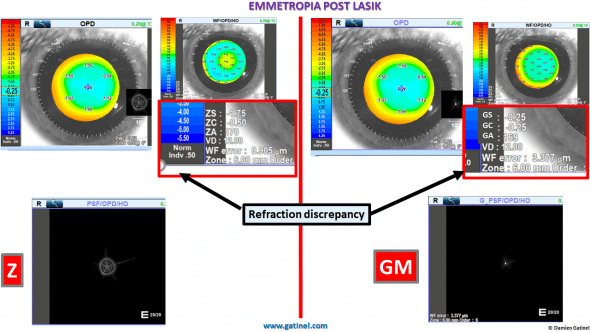
Refraction prediction discrepancy between wavefront decomposition methods: Zernike vs LD/HD with Gatinel Malet (GM) coefficients.
As you can see the PSF light distribution is exaggerated in the Zernike prediction as well as the refraction being far more myopic.
The comparison between the wavefront coefficients and their predicted metrics is instructive:
The Zernike decomposition suggests a mixture of low and high order aberration. The highest coefficient in the Zernike decomposition is that of defocus, despite the eye being emmetropic!
In the LD-HD decomposition, the tilt and defocus coefficients are negligible. In addition, there is no artificial reduction of the coma and spherical aberration coefficients, and this contributes to highlight the true clinically significant higher order aberrations at play.
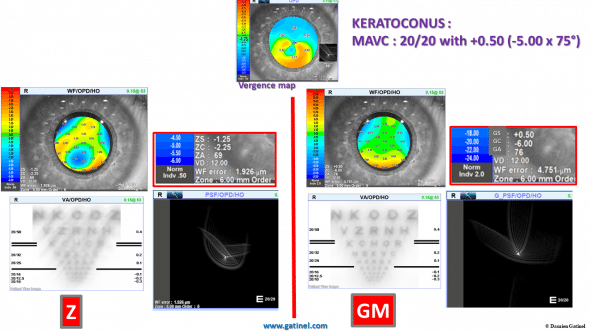
EXAMPLE 3:
This 28 yr old- male has developed right eye keratoconus after rubbing his eyes too often and vigorously.
The subjective refraction is +0.50 (-5 x 75°) and the best corrected visual acuity is 20/20.
Note the disparity between the predicted refraction and the better estimation of astigmatism and spherical equivalent with the LDHD method.
Here is the comparison between the wavefront coefficients charts:
Note the reduction of the tilt (or prism-like) aberrations and the highlighting of some high-order aberrations in the LDHD decomposition.
RELEVANCE TO Q-VALUE AND ASPHERICAL/CUSTOMIZED PHOTOABLATIONS:
This chart represents the comparison between the Zernike and GM coefficients’ changes between the two decompositions when asphericity is modulated (target Q varied between 0 and -0.9, for a +3D hyperopic correction).
The first graph allows to compare the variations of the defocus coefficients (Δz20 vs Δg20):

Comparison of the theoretical variations in the defocus coefficients (Δz20 vs Δg20) after the deliverance of a custom-Q hyperopic correction (+3 D) for various target asphericities (toward increased prolateness). Note the stability of the g20 defocus coefficient which is, as opposed to the z20 defocus coefficient, robust to the variations of the corneal asphericity.
In the LD/HD decomposition with GM coefficients, the defocus coefficient is almost unaffected. In the Zernike decomposition, interactions between spherical aberration and defocus result in a dramatic reduction of the defocus coefficient. This is not expected from a clinical standpoint, as the variations of the corneal asphericity should leave the paraxial (apical) corneal curvature unchanged. The LD-HD wavefront analysis method using the GM modes correctly reflects the expected results from a clinical viewpoint.
The second graph allows to compare the variations of the spherical aberration coefficients:
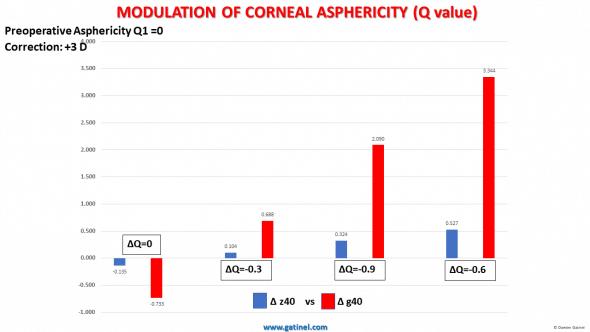
Variations of the spherical aberration coefficient after customization of the asphericity in hyperopic correction : Δz40 vs Δg40.
As expected, the variation of the asphericity induces a variation of the spherical aberration coefficients. The amplitude of the induced variation is reduced or minimized in the Zernike classification.
CONSEQUENCES:
ASPHERICAL (CUSTOM Q) ABLATIONS
As underlined above, aspherical photoablations (custom Q) have unexpected effects on the defocus coefficients when using Zernike coefficients to elaborate customized photoablations (read more about the relation between variations of asphericty and their effects on Zernike spherical aberration).
When correcting Zernike spherical aberration, unwanted low order correction will occur if no preoperative adjustment is made. Spurious refractive results can occur and this will oblige the surgeon to anticipate unwanted interactions between the low and higher-order wavefront component.
Similarly, the interactions between higher order (Z4+/-2) astigmatism and low order astigmatism (Z2+/-2) may reduce the accuracy of the optical refractive evaluation and subsequent correction.
This screenshot from the EX500 excimer laser (Wavelight/Alcon) in the Custom-Q mode enables the surgeon to visualize the expected changes in the wavefront for a specific aspheric correction.
In this example, the refractive correction is +2.50D, the initial asphericity is Q=0, the target asphericity is also 0 (no intended change in corneal asphericity). This correction incurs an expected variation in the defocus (noted c4 in a single index scheme) and spherical aberration (noted c12 in a single index scheme) coefficients.
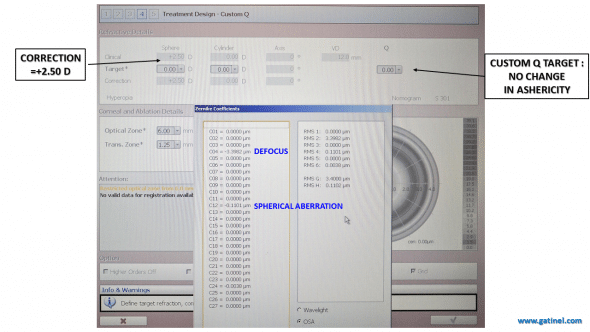
Effect on the Zernike coefficients of a customized aspheric correction of +2.50 D and no intended change in the corneal asphericity.
Now, let us examine the effect of the change in target asphericity (target Q is now -0.6). The refractive correction is unchanged. It results in an increase in the expected change in Zernike spherical aberration (as expected) but also a large change in the Zernike defocus (which is NOT clinically expected as no change in the planned refraction correction was made).
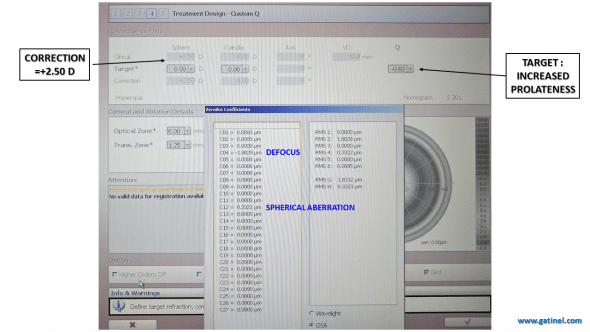
The modification of the corneal asphericity (toward increased prolateness) results in a large variation of the Zernike defocus coefficient, although the intended defocus correction is unchanged (+2.50 D).
Again, this variation in defocus is caused by the necessity to compensate for the low degree terms in r^2 « hidden » in the Zernike spherical aberration mode. Because it alters the peripheral curvature of the corneal contour, the intended asphericity modulation should mainly result in an alteration of the r^4 phase error (Seidel-like spherical aberration). The induction of the defocus is necessary to compensate for the defocus term present in the analytical expression of the Zernike spherical aberration.
TOPOGRAPHY GUIDED ABLATIONS
The correction of ocular optical ocular aberrations of corneal origin can be accomplished by the delivery of a customized photoablation called « topography-guided » or « topo-guided ». In this strategy, the surgeon aims at correcting both the refractive error and the corneal irregularities.
Based on some of the preoperative corneal characteristics (apical curvature, asphericity) which are obtained via corneal topography examination of the considered eye, an « ideal » corneal shape is defined.
This shape is a perfect rotationally symmetrical ellipsoid devoid of any irregularity. It would ensure a perfect optical quality if its power (which depends on the apical curvature) is adjusted to make the eye emmetropic (assuming no other source of optical imperfection within the internal ocular optical surfaces such as the posterior cornea or the crystalline lens).
This ideal surface is compared to the actual preoperative corneal topography of the operated eye: the difference between the two corresponds to the corneal irregularities which encompass both regular and irregular astigmatism and can be expressed as a Zernike coefficient expansion. This expansion corresponds to a theoretical wavefront error of corneal origin, which comprises low order astigmatism and higher order modes’ coefficients.
However, this approach will require the surgeon to perform some adjustments to the target refractive correction.
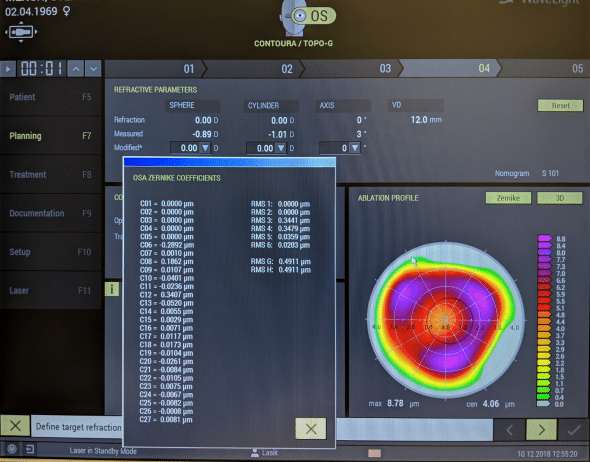
– Firstly, the refractive and corneal astigmatisms may differ (because of the presence of internal astigmatism). In our example, the software suggests altering the cylinder and axis of the refraction to the following values: -1.01 D x 3° (see the « Measured CYLINDER & AXIS » in the REFRACTIVE PARAMETERS box).
However, if the corneal astigmatism is estimated from the z(2,-2) and z(2,2) coefficients extracted from a Zernike decomposition of a theoretical corneal wavefront, it may not still be an accurate depiction of corneal astigmatism as some extra low order astigmatic terms may be « hidden » in the higher order astigmatism modes (e.g. z(4,-2), z(4,2), z(6,-2), z(6,2) ).
– Secondly, because of the presence of a defocus term in the Zernike spherical aberration mode, an adjustment of magnitude -0.89 D (added to the sphere obtained from subjective refraction) must be made to the corrected refractive sphere (see the « Measured SPHERE » in the REFRACTIVE PARAMETERS box).
The list of single scheme index Zernike polynomials corresponds to the predicted change induced by a customized topographic ablation.
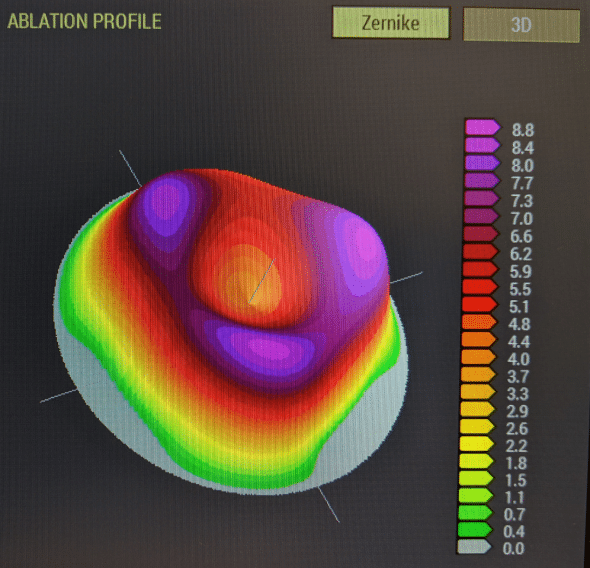
The reason for this adjustment can be deduced from the inspection of the profile of ablation restrained to the correction of higher order corneal aberrations which is shown on the right. Because of the correction of Zernike spherical aberration of corneal origin (coefficient c12, which corresponds to z40), an unintended but necessary low degree change is induced (equivalent to the amount of r^2 term – defocus within z40). This defocus is of a negative sign (induced myopia). This is why the software suggests altering the sphere correction by an amount of -0.89 D to avoid an under-correction.
This figure displays a 3-D plot of the ablation profile which aims at correcting higher order aberrations of corneal origin (mainly positive spherical aberration Z40 and trefoil Z3+/-3 modes). Note the central dip, caused by the parasitic defocus term embedded in the Zernike spherical aberration mode, which explains the unwanted induction of some myopic defocus (the overall profile grossly looks like a hyperopic ablation profile, not like a « pure higher order » correction profile which should be paraxially null or constant).
CONCLUSION:
The effect of customized ablations and topics related to the comparison between the total eye and corneal aberrations might be facilitated by methods which better segregate the true high and low order wavefront components. Better inferences can be made by clinicians and surgeons when using better « wavefront semantics ».
This may promote a better understanding and adoption of these cutting edge or customized techniques by the surgeons, and avoid unnecessary steps in treatment programming.
Watch the video:
See other relevant examples and material :
Pre and Post LASIK aberrations



Hi Len, thank you for your encouraging comments. I have presented an introduction to this work last year in Denver at the Wavefront Congress and ARVO (as a paper communication). I have submitted the continuation of this (clinical applications related to refraction prediction) to be presented at 2019 ARVO… I hope to see you there!
Hi Damien,
This is super interesting work. I look forward to learning more about it. There are some topics in my life that took several introductions before I really understood it. For example, Fourier transforms and physical optics was like that for me as a student. This will also probably take several redundant explanations. But just because something is difficult, does not mean it is unimportant. Quite the contrary. Do you plan to present this at Wavefront Congress or ARVO this year?
Take care,
Len