Réflexion sur miroirs courbes sphériques
Lois de la réflexion sur les miroirs
Connaître certaines lois de la réflexion de la lumière sur des miroirs courbes sphériques s’avère utile pour appréhender les fondamentaux de technologies comme la topographie cornéenne spéculaire, et comprendre la genèse des reflets lumineux que l’on peut observer lorsque l’on illumine l’œil, dont le plus simple à observer est le reflet cornéen, également appelé image de Purkinje I.
Comme pour les lois de la réfraction, les questions que l’on cherche à résoudre concernent la position du plan où se forme l’image (le reflet) et la taille de cette image (sa magnification).
L’œil oppose au trajet de la lumière trois surfaces qui agissent comme des miroirs convexes :la face antérieure de la cornée, la face postérieure de la cornée, la face antérieure du cristallin. Seule une surface agit comme un miroir concave : la face postérieure du cristallin. Le pourcentage de la lumière incidente réfléchie est proche de 5% pour la face antérieure de la cornée, et beaucoup plus faible pour les images formées par la réflexion sur les autres surfaces.
En vertu du principe de Huygens et du temps de parcours minimal imposé au parcours de la lumière, la réflexion d’un rayon sur une surface plane ne pose pas de problèmes. L’angle d’incidence avec la surface (où la normale au point d’incidence) est égal l’angle réfléchi.
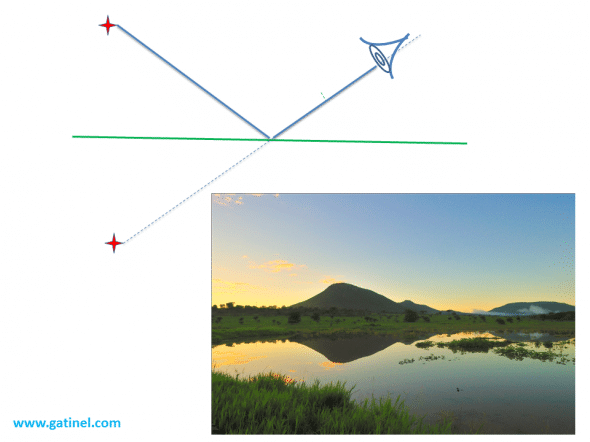
Réflexion plane (en haut). L’image réfléchie subit une inversion. L’œil qui observe le miroir dans une direction donnée fixe un point de l’image tel que le temps mis par la lumière depuis sa source jusqu’à la l’œil est minimal (équivalent au trajet en « ligne droite ». (en bas exemple de réflexion plane en milieu naturel)
Un rayon incident sur la surface lisse d’un miroir courbe forme un angle donné avec la normale à cette surface (que l’on peut considérer comme localement plane). Il est réfléchi selon un angle identique vis-à-vis de cette normale.Dans le cas des miroirs courbes, circulaires en section, la normale à la surface épouse le trajet du rayon de courbure local de cette section.
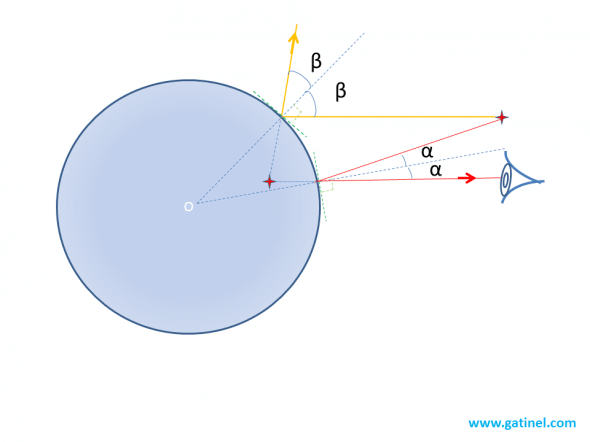
L’observateur et la source ne sont pas alignés avec le centre du miroir: les rayons lumineux qui atteignent l’observateur sont réfléchis selon un angle égal de part et d’autre de la normale à la surface au point de réflexion.
Miroir concave
Seule la face postérieure du cristallin (ou d’un implant) se comporte comme un miroir concave. Nous nous intéresserons à un système simple, un miroir concave circulaire où un rayon incident proche de l’axe optique est réfléchi. A ce stade, on s’intéresse à établir un lien entre l’angle d’incidence avec la normale à la surface réfléchissante, sa courbure (inversement proportionnelle à la valeur de son rayon R), et le trajet du rayon réfléchi.
En raison de la symétrie de révolution (représenté plus loin en coupe), on devine que tous les rayons incidents parallèles réfléchis à la même distance de l’axe optique se couperont sur l’axe optique. Il est donc essentiel de repérer l’intersection d’un rayon incident parallèle à l’axe de symétrie du miroir (l’axe optique), avec l’axe optique.
Cette démarche vise ainsi à déterminer la position de l’image formée par la réflexion avec le miroir d’un point situé à l’infini, pour des rayons proches de l’axe optique.
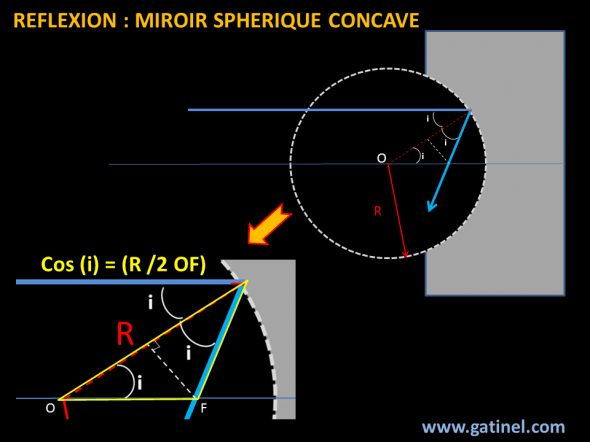
Quand un rayon incident est réfléchi par un miroir sphérique, il forme un l’angle d’incidence i vis-à-vis de la normale à la surface du miroir. Par définition, l’angle réfléchit forme un angle égal à i vis-à-vis de cette normale, qui passe par le centre de courbure du miroir. Le point d’intersection avec l’axe optique (F) permet de dessiner un triangle isocèle, dont le grand côté (hypothénuse) est OF
On peut établir à partir de la figure ci-dessus la loi suivante :
OF = R / (2 x cos (i) )
Comme l’angle i varie avec la distance du rayon incident à l’axe, on déduit de cette égalité que la position du point F varie avec la hauteur du rayon considéré. Le miroir sphérique n’est pas un système stigmatique ; l’image d’un point n’est pas un point, sauf à considérer un petit faisceau de rayons incidents.
Quand i est petit, on peut alors écrire : OF = R/2 car cos (i) tend vers 1.
Pour les petits angles d’incidence (les rayons proche de l’axe optique), on peut établir que le foyer du miroir, où se concentrent les rayons, est situé à une distance égale à la moitié du rayon de courbure du miroir. L’image formée par le miroir est située dans un plan avant de celui-ci, et inversée
Miroir convexe
On peut construire une figure équivalente, cette fois-ci avec un miroir convexe, et en déduire la même égalité que précédemment. La construction géométrique révèle que le foyer est situé cette fois ci « en arrière » du sommet du miroir. La position de l’image est également située « en arrière » du miroir sphérique. Ceci ne doit pas choquer: l’image est virtuelle, mais elle peut tout à fait être « captée » par l’oeil, ou un capteur photographique. Cela signifie que les rayons émis en réflexions « semblent provenir » du plan de formation de l’image (l’oeil ou le capteur ne peuvent pas savoir que les rayons ont subis une réflexion préalable).
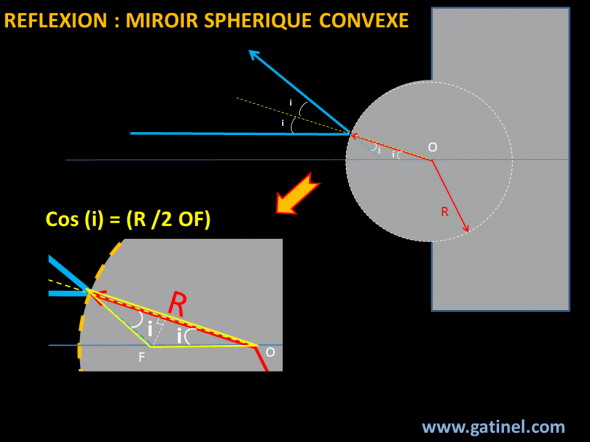
Quand un rayon incident est réfléchit par un miroir sphérique convexe, il forme un l’angle d’incidence i vis-à-vis de la normale à la surface du miroir. Par définition, l’angle réfléchit forme un angle égal à i vis-à-vis de cette normale, qui passe par le centre de courbure du miroir. Le point d’intersection avec l’axe optique (F) permet de dessiner un triangle isocèle, dont le grand côté est R.
Position de l’image réfléchie
Le schéma suivant pose les bases du problème : on cherche la position I de l’image d’un point source O situé sur l’axe optique. Avec quelques approximations sur les petits angles (la tangente de l’angle est égale à l’angle en radians, et le cosinus d’un petit angle est très proche de 1), on peut établir une formule de conjugaison qui permet de calculer la position de l’image réfléchie.
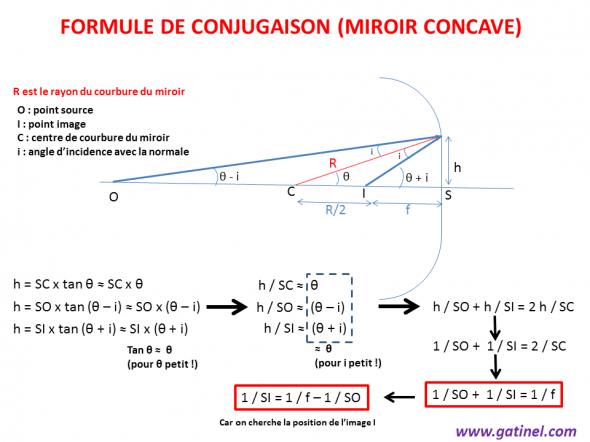
Sur le schéma, le rayon issu de O rencontre la surface du miroir concave à une hauteur h. Il se réfléchit et coupe l’axe optique en I (attention : I n’est pas exactement situé à la distance f, comme pour un rayon incident parallèle à l’axe optique).
Pour effectuer des calculs avec cette formule, il est important de considérer les distances comme des grandeurs algébriques : vers la gauche à partir du sommet, les distances sont des quantités négatives, vers la droite, positives.
Pour un miroir convexe, la formule est identique, mais le signe pour la valeur du rayon de courbure est négatif.
Il est intéressant de noter que cette formule ressemble à la formule de vergence, mais que n’y intervient aucune valeur d’indice de réfraction, puisque la propagation de la lumière s’effectue en réflexion, dans le même milieu.
Ces formules permettent de calculer la position des reflets oculaires (images de Purkinje).
Exemple :
On cherche à connaître la position de l’image d’un objet source situé à 40 cm de la surface de la cornée, dont le rayon de courbure est 8 mm. Le foyer du miroir est donc situé à la moitié de cette distance (4 mm).
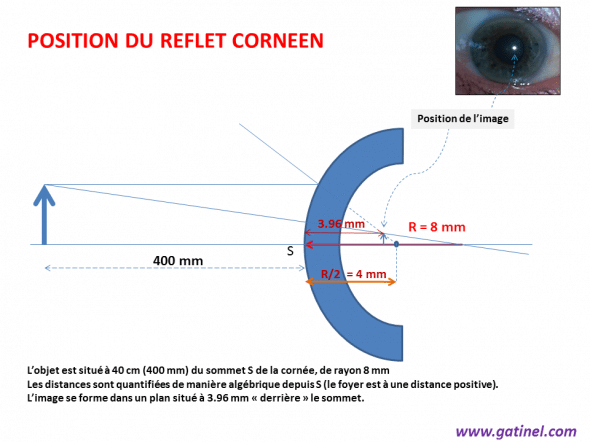
Schéma permettant le calcul de la position d’une image réfléchie par la cornée (ex: image d’une source lumineuse brillante en réflexion sur le do^me cornéen)
On peut donc écrire :
1/(distance image) = 1/f – 1/(distance objet)
1/(distance image) = 1/4 – 1/-400 =101/400
Distance image =400/101 = 3.96 mm
L’image (virtuelle) apparait située dans un plan postérieur au miroir, et n’est pas inversée (contrairement au cas de la réflexion par un miroir concave – quand l’objet est situé avant (plus loin) du foyer.

Vous présentez certainement des dysphotopsies: plus d’informations ici: https://www.gatinel.com/chirurgie-de-la-cataracte/dysphotopsies/
Bonjour docteur. Il y a 4 mois j ai été opérée de la cataracte des 2 yeux à 15 jours d interval.j ai signalé à mon ophtalmologie une gêne dur la vision latérale. Je vois des cercles noirs. Ce qui a pour conséquences de me faire perdre l équilibre. Mon ophtalmologie m à fait un IRM cerebral. Qui n ai rien révélé d anormal.donc mon ophtalmologie ne m à pas fait de diagnostic ! ,et m envoie chez un orthopiste Quand pensez-vous !