Huygens (Principe de)
Le principe de Huygens concerne la propagation de la lumière sous forme d’ondelettes transmises et re émises successivement. C’est à l’astronome et mathématicien hollandais Christian Huygens (1629-1695) que l’on doit la première théorisation du front d’onde. Celle-ci fut inspirée par les propriétés des ondes mécaniques, dont il tira le principe des ondes « enveloppes », qui depuis porte son nom.
Analogie mécanique
En observant le fait qu’une vaguelette produite à la surface de l’eau après la chute d’un caillou se propage par action de proche en proche, il comprit que tout point de cette surface atteint par la vague devait son mouvement à l’action directe de points voisins et non pas à l’action de la source primaire (lieu de la chute du caillou). Dans cette théorie, tout point atteint par l’onde agit alors comme une source secondaire qui, à son tour, réémet une ondelette en direction de son voisinage. De ce fait, connaître l’état de l’ébranlement de la surface de l’eau à un instant donné permet de prédire sa position future : il n’est pas forcément besoin de connaître les caractéristiques de l’impulsion initiale.
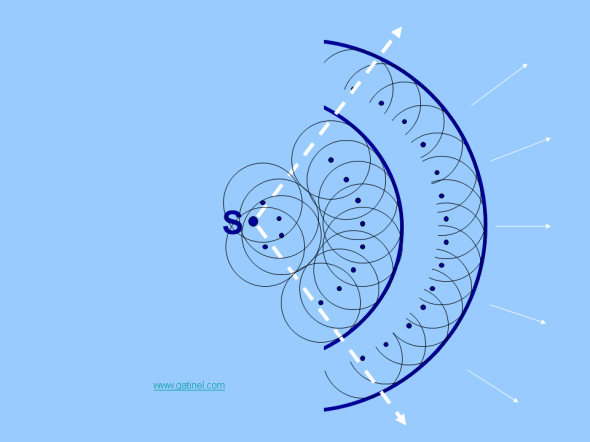
Le principe de Huygens repose sur la restitution par les points adjacents de l’impulsion de la source initiale sous forme d’ondelettes.
Ondelettes lumineuses
Huygens transposa ces constatations à la lumière et postula qu’une source lumineuse émettait des impulsions successives, donnant naissance à une perturbation localisée sur une surface appelée « front d’onde », qui se propageait dans un milieu spécifique (« l’éther »). A l’époque de Huygens, la notion de champ électromagnétique n’était pas connue, et les ondes lumineuses devaient nécessairement avoir un « support » pour ce propager. Huygens concevait le processus de propagation des ondelettes lumineuses comme des vibrations mécaniques dans un milieu élastique.
Si un front d’onde possède une certaine position à un instant donné t, sa position ultérieure est déterminée comme l’enveloppe des ondelettes émises à cet instant t par les points sources secondaire distribuées sa position initiale. Dans un milieu homogène, les ondes conservent leur caractère plan ou sphérique.
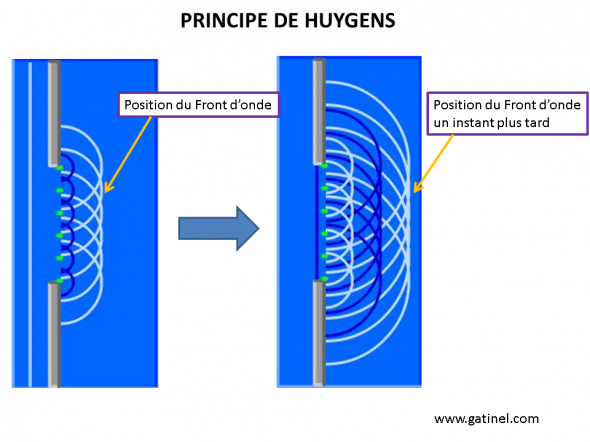
La propagation d’un front d’onde à un instant ultérieur peut se déduire de la position des ondelettes à un instant précédent.
Interférences et propagation lumineuse
Le principe de Huygens a été complété et formulé mathématiquement par Fresnel au début du 19e siècle, en y incluant le concept d’interférences; ce concept explique qu’il n’y a pas d’onde ré émise « vers l’arrière » lors de l »ébranlement lumineux » de sources contiguës. En effet, dans un milieu homogène dense, il y a peu ou pas de lumière diffusée latéralement ou en arrière. L’atmosphère terrestre contient plusieurs millions de molécules dans un cube dont l’arrête serait égale à une longueur d’onde lumineuse visible (ex: 500 nm). Ceci est lié aux dimensions des molécules, de l’ordre du nanomètre, alors que l’onde lumineuse visible est de l’ordre du micron.
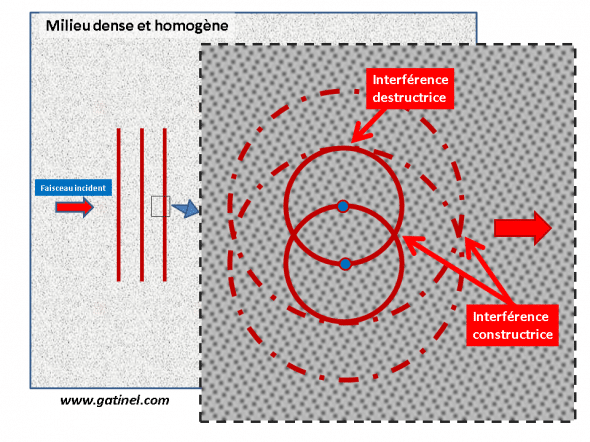
Une onde plane se propage dans un milieu dense et homogène, composé de nombreux atomes contigus, représentés ici schématiquement par des « points ».Dans la direction perpdendiculaire à la propagation, on peut former autant de paires d’atomes séparés d’une demi longueur d’onde (les atomes sont environ mille fois plus petits que la longueur d’onde concernée). En vertu du principe de Huygens, chaque atome re émet l’onde incidente dans toutes les directions. En dehors de la direction même de la propagation, il existe des interférences destructrices pour chacune de ces paires d’atomes qui explique l’absence de diffusion latérale de la lumière. En vertu du principe de conservation de l’énergie, il ne pourrait y avoir d’interférences constructives dans toutes les directions ! Au niveau des atomes, la lumière est absorbée et re émise par les électrons. Ce phénomène est à l’origine de modifications de la « phase » de l’onde diffusée, qui peut alors apparaître comme ralentie dans le milieu (l’indice de réfraction est proportionnel au ralentissement de l’onde transmise). Dans un milieu peu dense (ex : haute atmosphère), du fait de la raréfaction des atomes et molécules, les phénomènes d’interférence disparaissent. Il existe alors, au hasard des « rencontres » entre lumière et atomes, des réemissions latérales, dont on peut montrer qu’elles sont proportionnelles à la fréquence (puissance 4) de l’onde lumineuse. Le bleu (haute fréquence) est plus diffusé que le rouge, et ceci explique la couleur du ciel: nos yeux perçoivent une dominante bleue car cette longueur d’onde est plus diffusée latéralement, donc vers le sol.
Principe de Huygens et loi de Snell-Descartes
En examinant les conséquences du principe de Huygens, il est important de réaliser que les fronts d’onde émis consécutivement sont séparés par des intervalles de temps égaux. Cette propriété permet de prouver la loi de la réfraction de Snell (appelée Snell-Descartes en France). La réfraction survient quand le front d’onde rencontre un autre milieu et que sa vitesse de propagation y diminue.
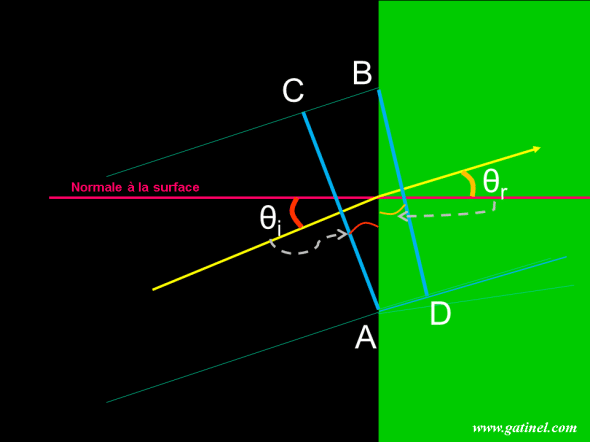
Dans le milieu de gauche, le front d’onde se déplace à la vitesse vi. A droite, sa vitesse (vr) diminue. Le front d’onde forme un angle θi avec la normale à la surface, et est dévié d’un angle θr après réfraction. En vertu du principe de Huygens, le temps mis par la lumière pour aller de C à B est le même que celui pour aller de A à D. Ce temps est égal à la distance divisée par la vitesse, et l’on peut poser : CB/vi = AD/vr D’après la géométrie de la figure, et en observant que θi est égal à l’angle (CAB) et que θr est égale à l’angle (ABD) on peut exprimer que la distance CB= AB sinus (θi) et la distance AD = AB sinus (θr). La première équation devient AB sinus (θi) /vi = AB sinus (θr)/vr. On peut simplifier par AB et multiplier par une constante c (vitesse de la lumière dans le vide) et l’on obtient : sinus (θi) c/vi = sinus (θr) c/vr. Le rapport entre la vitesse de la lumière dans le vide et la lumière dans le milieu considéré est égal à l’indice de réfraction de ce milieu : ni = c/vi et nr = c/vr On obtient finalement : ni sinus (θi) = nr sinus (θr)
La loi de Snell permet de calculer le tracé d’un rayon réfracté, à partir de l’angle formé par l’angle incident avec la normale à la surface et la valeur des indices de réfraction de chacun des milieux.

La loi de Snell-Descartes permet de calculer le tracé de rayon lumineux au travers de surfaces réfractives. Cette loi est un pilier de l’optique géométrique. Elle est conforme au principe de Fermat, qui stipule qu’entre deux points, la lumière emprunte le trajet de durée minimale (et non de distance minimale).
Principe de Huygens et front d’onde
Ainsi, le principe très général de Huygens eut être ré interprété dans le cadre de la théorie ondulatoire (ondes électromagnétiques) de la lumière. Supposons une source lumineuse monochromatique (S) dans un milieu homogène isotrope. Elle émet des ondes lumineuses, qui se propagent le long des rayons dans toutes les directions : en chacun des points de l’espace proche de la source gagné par l’onde lumineuse, l’état du champ électromagnétique oscille (à la fréquence de la source), entre une valeur maximale et une valeur minimale. A un instant donné, tous les points situés à une distance identique de la source sont dans le même état (ils sont « en phase »).
Quand la source est placée dans un milieu isotrope, l’enveloppe des points situés à même distance de la source épouse une forme sphérique dans l’espace (et circulaire dans le plan). Le front d’onde est sphérique, et puisque les ondes s’éloignent de la source, il est divergent. Au fur et à mesure que l’on s’éloigne de la source, le rayon de courbure augmente (une même portion de front d’onde est de plus en plus plate). Si l’on est assez loin de la source, un instrument d’observation pourra collecter une portion de la surface d’onde dont la courbure pourra être considérée comme nulle (plane).
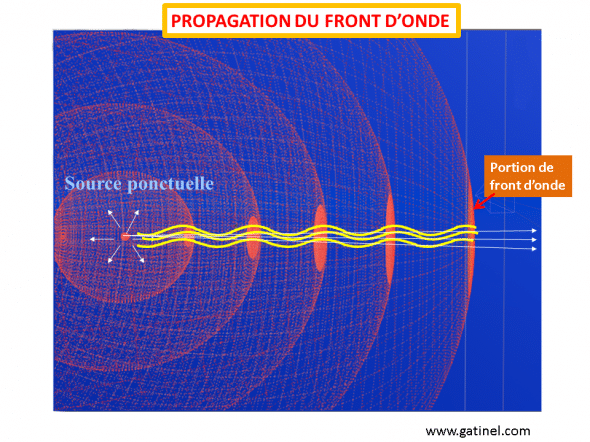
La source initiale de lumière propage un front d’onde qui est localement perpendiculaire aux rayons lumineux (propriété de « congruence normale »). Les rayons provenant d’un point source sont perpendiculaires à la sphère centrée sur la source. A distance de la source, une portion de front d’onde peut être considérée comme « plane ».
Le front d’onde est l’enveloppe qui relie ces points « en phase ». plane quand les rayons se propagent de manière parallèle, elle est sphérique et en expansion dans le cadre d’un front d’onde divergent. Elle est également sphérique mais tend à se collapser vers un point central en cas de front d’onde convergent.

Exact, merci pour la lecture attentive, la typo est corrigée!
A la 5e ligne du commentaire du schéma de la loi de Snell-Descartes, thêta i ne doit-il pas être remplacé par thêta r dans la phrase « et que thêta i est égale à l’angle (ADB) » ?
Amitiés