Pouvoir optique paraxial de l’oeil
Le pouvoir optique de l’œil est celui du couple formé par la cornée et le cristallin.
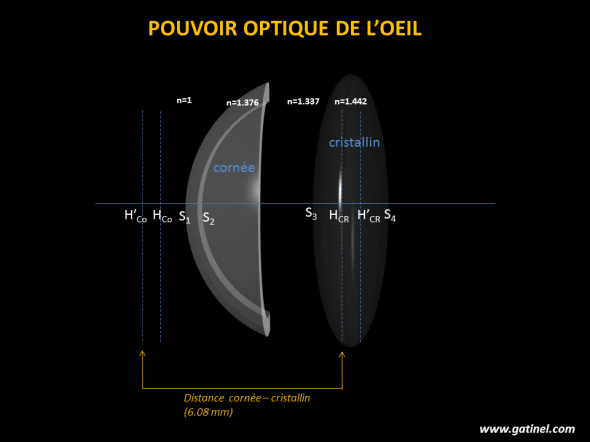
Il ne suffit pas d’additionner ce qui a été calculé (voir pages concernées) pour le pouvoir optique de la cornée (Dco) et le pouvoir optique du cristallin (Dcr), car il faut également tenir compte de la distance entre ces éléments. Nous choisirons un oeil modèle où la profondeur anatomique de la chambre antérieure (de l’endothélium à la face avant du cristallin) est égale à 3.05 mm.
La distance « optique » est, dans un calcul paraxial, la distance entre le plan principal image de la cornée (H’co) et le plan principal objet du cristallin (Hcr) : distance optique = H’coHcr
Muni de ces données, on peut calculer la puissance optique de l’oeil assimilé à un système centré (cornée + cristallin)
Le pouvoir optique de l’oeil entier correspond au couple centré de la cornée et du cristallin.
Calcul de la puissance (vergence) de l’oeil entier
En utilisant la formule de Gullstrand, le pouvoir optique de l’œil est égal à :
Do = Dco + Dcr – (H’coHcr/nhaq)* Dco*Dcr
Il faut calculer la distance H’coHcr
Celle-ci est égale à :
H’coHcr = H’coS2 + S2S3 + S3Hcr
= 0.6101 + 3.05 + 2.42 = 6.08 mm
On peut alors cacluler Do:
Do = 42.17 + 21.82 – 0.00608/1.337 – 42.17 *21.82 = 59.80 D ≈ 60 D
La puissance totale de l’oeil (cornée+cristallin) est donc proche de 60 Dioptries.
Détermination des distances focales
Les distances focales de l’œil découlent du calcul de la vergence de l’oeil, système centré équivalent à l’ensemble cornée + cristallin:
Distance focale objet :
fo = -1/Do =-1/60 = -0.01667 m = 16.67 mm
Distance focale image:
f’o = 1.336/Do = 1.336/60 = 0.02227 = 22.27 mm
Cette distance focale image ne doit pas être confondue avec la longueur axiale: elle correspond à la distance séparant le plan principal image de l’oeil du foyer. Il reste à déterminer la position des plans principaux de l’oeil entier
Détermination des plans principaux de l’œil entier
On détermine la position du plan principal objet à partir du plan principal objet de la cornée et du rapport des distances focales entre l’oeil et le cristallin.
Plan principal objet :
HcoHo = H’coHcr fo/fcr = 6.08 x ( -16.67/-61.27) = 1.65 mm
De même, on peut calculer la position du plan principal image:
Plan principal image
H’crH’o = -H’coHcr f’o/f’co = -6.08 x (22.27/31.70) = 4.27 mm
L’écart entre les plans principaux est donné par :
HoH’o = HoHco + HcoH’co + H’coHcr ° HcrH’cr +H’crH’o
=-1.65 + 0.001+6.08 +0.18 – 4.27 = 0.33 mm
Détermination de la position des plans principaux par rapport aux éléments anatomiques de l’œil
On choisit le sommet de la cornée S1 pour repérer la position du plan principal objet de l’oeil Ho
S1Ho = S1Hco + HcoHo = -0,0583 + 1,65 ≈ 1.60 mm
S1H ‘o = S1S2 + S2S3 + S3S4 + S4H’cr + H’crH’o = 0.55 + 3.05 + 4 -1.4 -4.27 ≈ 1.9 mm
Il est intéressant de noter que la profondeur de la chambre antérieure de l’oeil intervient dans le calcul.
De fait on retrouve (aux approximations près): HoH’o = 1.9 – 1.6 = 0.3 mm
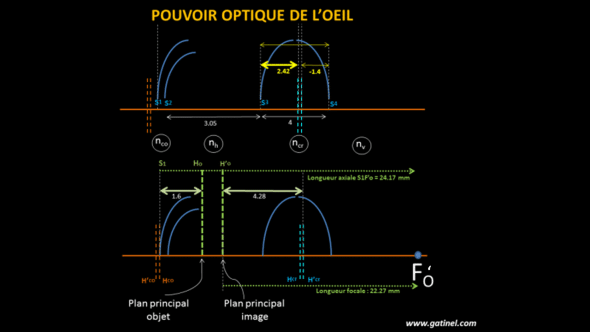
Ce schéma permet de repérer la position des éléments cardinaux de l’oeil entier. La distance entre le plan principal objet et le plan principal image de l’oeil entier est de 0.3 mm (les distances ne sont pas à l’échelle).
La distance du foyer objet vis-à-vis de la cornée est :
S1Fo = S1Ho + HoFo = 1.6 – 16.67 = 15.07 mm
La distance du foyer image vis-à-vis de la cornée
S1F’o = S1H’o + H’oF’o = 1.9 + 22.27 = 24.17 mm
Dans ce modèle d’oeil théorique, en cas d’emmétropie, la distance de la rétine (plan des photorécepteurs) à la face antérieure de la cornée doit être égale à 24.17 mm. Cette valeur peut être assimilée à la longueur axiale de l’oeil emmétrope qui aurait une cornée et un cristallin conforme aux données numériques utilisées pour les calculs de cette page.
Petite erreur d’opérateur dans la formule
« Do = 42.17 + 21.82 – 0.00608/1.337 – 42.17 *21.82 = 59.80 D ≈ 60 D »
qui devrait s’écrire:
Do = 42.17 + 21.82 – 0.00608/1.337 * 42.17 *21.82 = 59.80 D ≈ 60 D »
^
^
Du super boulot votre site ! Bravo et merci d’avoir mis tout ceci en libre consultation !