Myopie: réfraction et longueur axiale
La myopie est une amétropie qui est caractérisée par une longueur axiale oculaire excessive vis-à-vis de la puissance réfractive des éléments optiques de l’œil (cornée et cristallin).
Peut-on quantifier l’effet de l’allongement de l’œil sur la réfraction oculaire ? De quel ordre est l’effet sur la longueur de l’oeil l’augmentation de la myopie d’une dioptrie? De combien de dioptries de myopie un millimètre d’élongation oculaire est-il responsable?
Pour répondre à ces questions, on peut réaliser le schéma suivant et accomplir quelques simplifications : l’œil myope est par définition tel que la rétine est conjuguée avec le punctum remotum qui est à une distance finie (L) du plan principal antérieur P. L’image de l’objet situé au punctum remotum (noté PR) est formée sur la rétine, située à une distance L’ du plan principal postérieur P’ (les plans principaux sont conjugués et tels que leur grandissement est égal à 1). L’objet source (situé au punctum remotum) est dans l’air (n=1), et son image se forme dans un milieu dont l’indice de réfraction est celui du vitré (n’ = 1.336).
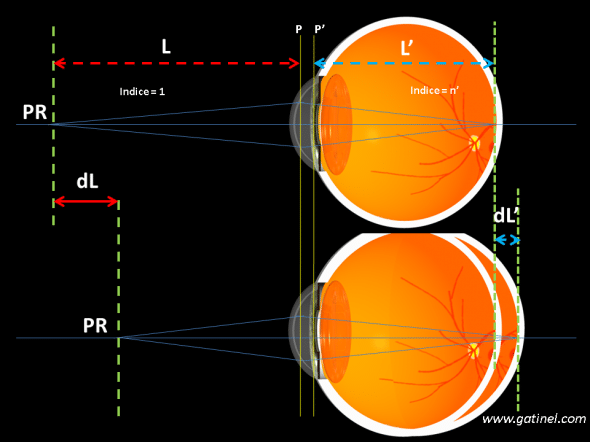
Relation entre longueur axiale et myopisation. Le schéma représente un œil myope (en haut), dont on augmente la longueur axiale (en bas), sans en modifier les autres paramètres biométriques (même cornée, même cristallin). L’accroissement de la longueur axiale d’un élément dL’ provoque une modification de la position du punctum remotum: l’inverse de la distance dL est égal à V0, qui est le changement de vergence provoqué (myopisation).
En utilisant les relations de vergences (et en prenant garde au respect des conventions de signes pour l’expression des distances), on peut écrire que la vergence de l’œil (V) est égale à : n’/L’ + (n/-L),
soit V = n’/L’ – n/L (1)
Le second terme de cette expression est la vergence de l’objet, situé dans l’air (n=1) que l’on peut écrire V0 = 1/L. L’expression (1) devient :
V = n’/L’ – V0,
D’où l’on obtient :
V0 = n’/L’ – V (2)
Signalons que pour un objet situé à l’infini, un œil emmétrope a une vergence égale à n’/L’ (V0 égal 0 car L est infini)
Que se passe-t’il si on augmente la longueur axiale d’une quantité dL’ ? Ceci provoque une petite variation de la distance du Punctum Remotum que l’on note dL, et donc de la vergence de l’objet dV0 (= 1/dL).
On cherche à estimer de combien varie V0 (qui est le changement de vergence lié au rapprochement du PR) avec dL’ (augmentation de la longueur axiale de l’œil)?
Nous avons établi : V = n’/L’ – V0 où V est une constante liée aux caractéristiques de l’œil concerné (la vergence de l’œil entier est en pratique égale à l somme des vergences respectives de la cornée et du cristallin). On considère cette expression comme une fonction qui relie L’ (la variable) et V0
Pour évaluer l’effet d’une petite variation de L’ (désignée par dL’) on peut dériver V0
par rapport à dL’ dans l’expression (2) établie précédemment (V0 = n’/L’ – V)
ce qui donne : dV0 /dL’= n’/-L’ 2
donc: dV0 = n’ dL’/-L’ 2
Pour un œil emmétrope, L’=n’/V (car L est à l’infini) et on obtient au final en remplaçant L’ par n’/V :
dV0 = dL’ V2 /n’ (3)
Le changement de vergence est donc égal au produit de l’accroissement de longueur axiale multiplié par le carré de la puissance oculaire initiale, divisé par n’.
Exemple numérique : si un œil possède une vergence de 60 D s’allonge de 1mm, quelle est la variation induite de la vergence de l’objet (soit l’erreur réfractive induite ?) :
dV0 = 0.001 x 602 / 1.336 = 2.70 D.
On peut donc estimer qu’une augmentation de la longueur axiale de 1 mm provoque donc une myopie d’environ -2.75 D, et ceci est assez bien corroboré à ce qui est observé en pratique clinique, où il est toutefois difficile d’établir une corrélation forte entre longueur axiale et myopie pour les myopies faibles (inférieures à -4D). Ces myopies sont en effet liées à une « dysharmonie » entre longueur axiale et vergence.
A la lumière de ces données, on peut imaginer que la Nature ait choisit un autre mécanisme pour permettre aux yeux de voir net de près, consistant en une élongation réversible du globe oculaire : un allongement de 1 mm de l’œil suffit en effet pour induire un changement de vergence de 2.75 D, permettant à un œil emmétrope de voir net à 1/2.75 soit 36 cm, qui est une distance confortable de lecture.
On peut aussi postuler qu’une réduction chirurgicale de la myopie consistant à « raccourcir » l’œil pourrait utiliser comme règle que pour chaque mm de réduction de la longueur axiale, la myopie est réduite d’environ 2.70 D.
Dans cet exemple, il existe une différence importante de réfraction (anisométropie) entre l’oeil droit et l’oeil gauche d’un même patient myope :
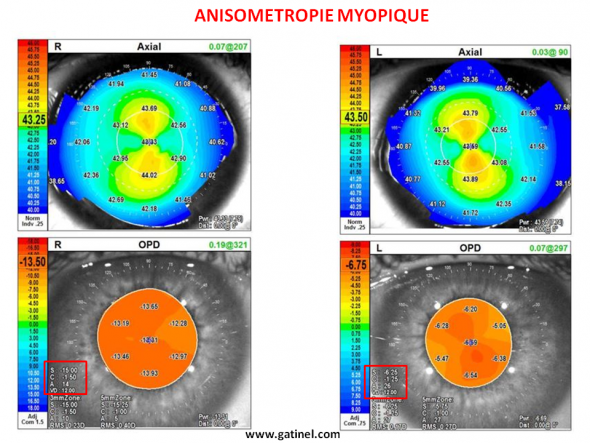
Cartes topo aberrométriques (OPD Scan III, Nidek) d’un même patient. L’oeil droit (R) présente une myopie forte (-15.75 D =équivalent sphérique). Du côté gauche (L), la myopie est beaucoup moins prononcée (équivalent sphérique = -7 D) La topographie cornéenne révèle des cornées dont le profil kératométrique est remarquablement similaire. La différence de réfraction provient quasi exclusivement de la différence de longueur axiale.

La mesure de la longueur axiale par biométrie interférométrique (IOL Master 700, Zeiss) révèle une différence de longueur axiale de 3.71 mm entre l’oeil doit (longueur axiale = 29.34 mm) et l’oeil gauche (longueur axiale = 25.63 mm).
L’exemple suivant est emprunté à un autre cas d’anisométropie (différence de réfraction entre les deux yeux d’un même sujet). L’œil droit est emmétrope (pas de correction pour une vision nette de loin), et l’œil gauche hypermétrope (environ +2.50 D). Comme prédit par la théorie, la différence entre les longueur axiales respectives de l’œil droit et de l’œil gauche est pratiquement égale à 1 mm.
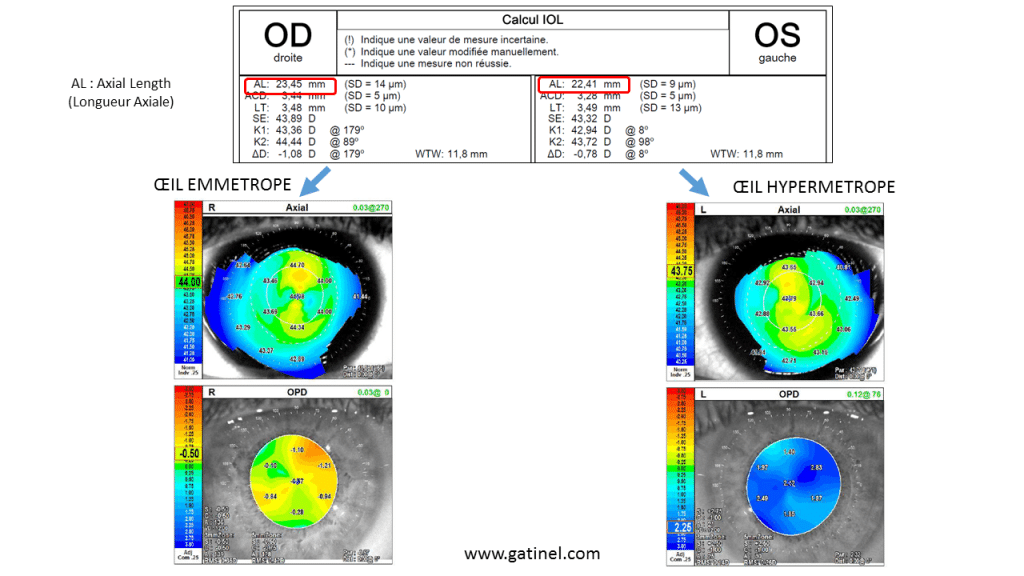
La différence de longueur axiale entre l’œil droit et l’œil gauche est proche d’un millimètre: la différence de réfraction (en équivalent sphérique) est de +2.50 D. L’œil gauche est hypermétrope car sa longueur axiale est insuffisante, et l’image formée sur la rétine est floue.
Dans ce nouvel exemple, la puissance cornéenne centrale (vergence), estimée par la kératométrie, est identique entre deux yeux qui diffèrent notablement en terme de longueur axiale (3 mm).
Le premier oeil, le plus long, est myope (environ 6.50 D), et le second, le plus court, hypermétrope (environ +3 D). Une différence de longueur axiale de 3 mm correspond comme le prédit la théorie à une différence de vergence proche de 10D.
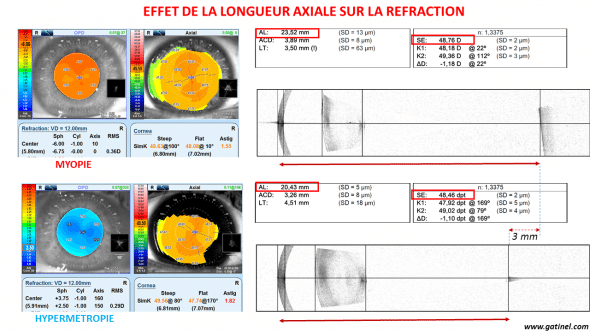
L’œil myope, en haut, présente une longueur axiale excessive vis à vis de la vergence du couple « cornée + cristallin ». En revanche, l’œil hypermétrope présente une longueur axiale insuffisante. Les deux yeux présentent une vergence cornéenne similaire. L’effet du cristallin (qui n’occupe pas la même position vis à vis de la cornée dans les deux cas) est probablement négligeable au regard de l’importante différence de réfraction entre les deux yeux.
Les opérations de la myopie consistent classiquement en un remodelage cornéen (destiné à réduire la vergence cornéenne d’une valeur égale à celle de la magnitude de la myopie). En sculptant la cornée (LASIK ou PKR), le laser en réduit l’épaisseur; ceci induit une réduction effective de la longueur de l’œil! Toutefois, cette réduction est de l’ordre de quelques dizaines de microns (la formule de Munnerlyn indique une quinzaine de microns par dioptrie de myopie traitée sur une zone optique de 6 mm). Pour chaque dioptrie traitée, l’oeil est donc plus « court » de 15 microns;
En utilisant la formule (3), on peut estimer le changement induit par ce raccourcissement de 15 microns à 0.04 D, ce qui est négligeable en pratique.
La longueur du segment externe contenant le pigment photosensible des photorécepteurs de la fovéa (cônes) est d’environ 50 microns soit 0.000005 mètres : que la lumière soit focalisée à l’avant ou à l’arrière de ces segments ne modifie pas en théorie leur activation. En utilisant la formule précédente (3), on peut convertir cette « tolérance spatiale » en « tolérance de vergence » qui vaut…. : 0.13 D (soit un demi quart de dioptrie). Cette valeur est justement du même ordre que la valeur minimale de modification de vergence à laquelle l’œil est sensible !
En pratique clinique, on observe parfois une réduction de la myopie (ou une hypermétropisation) d’environ 1 Dioptrie en cas d’œdème maculaire aigü : le « gonflement » du tissu rétinien résulte en une avancée du plan des photorécepteurs d’environ 200 à 400 microns (donc un raccourcissement de la longueur de l’œil), ce qui est conforme au changement réfractif observé.
Estimation du diamètre la tache de défocalisation
Quel est le diamètre la tache de défocalisation rétinienne induite par la myopie? Celui-ci dépend de la magnitude de l’erreur réfractive et du diamètre pupillaire.
On peut réarranger l’équation (3) de manière à exprimer l’élongation axiale (en mm) en fonction de l’erreur myopique (en dioptrie)
n’ dV0 / V2=
V2 /n’
dL’ = dV0 n’ / V2
Soit dL’ = 0.371 dV0 : 1 Dioptrie de myopie induit 0.371 mm d’élongation axiale pour un oeil dont la vergence moyenne est de 60 D. Pour un tel oeil, la longueur focale effective (LFE) est proche de 22 mm, avant élongation d’une valeur de dL’.
En utilisant la méthode des triangles identiques (cf schéma suivant), on peut poser que le diamètre de la tache de défocalisation (dB) est égal à :
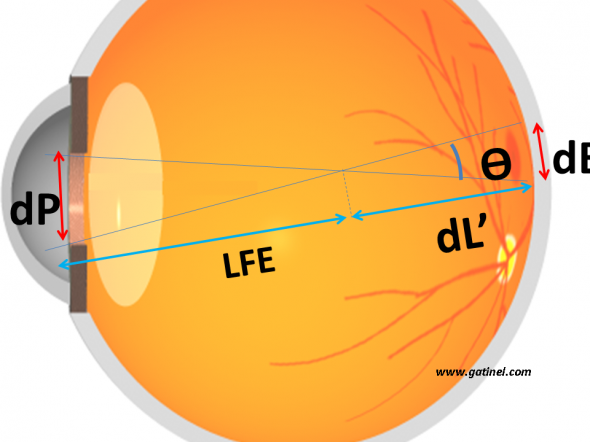
Le diamètre dB de la tache de défocalisation peut être estimé à partir du rapport entre le diamètre de la pupille d’entrée, la longueur focale effective (EFL) et dL’, l’allongement rétinien induit par l’erreur réfractive
dB = 0,371 x dP x dL’/22 soit 17 microns pour un diamètre pupillaire de 1mm et une erreur (myopie) d’1 dioptrie.

Les cellules souches végétales sont de nos jours la solution idoine pour le traitement de la myopie, puisque en dehors du décollement rétinien la myopie entraine la destruction des fibres visuelles par excavation papillaire qu’aucun traitement convention ne peut réellement gérer.
Bonjour, j’ai un problème de compréhension concernant le chromatisme dans l’oeil. En ordre de grandeur : la focalisation d’un oeil correspond à une puissance de 60 dioptries. En prenant un nombre d’Abbe maximum de 60 on va trouver un chromatisme d’au moins 1 dioptrie. On va donc avoir un écart de focalisation entre le bleu et le rouge de l’ordre de 250 microns.
Comment se fait-il que nous voyons pourtant une image nette dans toutes les couleurs.
Pouvez-vous m’éclairer sur cette question ?
Merci d’avance pour votre aide
IL est peu probable voire impossible que l’inversion de la correction ait provoqué cela. Les yeux myopes sont plus longs, et peuvent paraître plus « gros », et vous vous êtes peut être rendue compte de cela de manière « fortuite ».
Bjr,
Je suis allée chez l’opticien avec l’ordonnance de mon ophtalmo et l’opticien a trouvé une amélioration du fait qu’il a commandé les verres et a effectué la monture. Cependant en portant les lunettes sur les écrans je me suis aperçu qu’il y avait un probleme j’avais mal à l’œil gauche et quelques jours plus tard mon oeil a grossi comparé à celui droit. (je suis myope)
Mon ophtalmo m’a dis que l’opticien avait inversé les verres. Du coup l’opticien à recommander des verres et les a remis à sa place.
Concernant mon oeil gauche est ce qu’il va rester comme ça ou pas ? Car c’est un complexe.
Merci de votre réponse
Le facteur déterminant pour la survenue du décollement de rétine est effectivement la longueur axiale. Le degré de myopie n’est pas conditionné (uniquement) à la longueur axiale, mais également à la puissance optique de la cornée (une cornée puissante peut induire une myopie alors que la longueur axiale est peu excessive, statistiquement, et inversement).
Bonjour Docteur,
Je ne comprend pas bien les exemples. Certains yeux ont une myopie faible d’environ -2.50 et une longueur axiale de 26.5 mm (page sur les myopies) environ alors qu’un autre -6.50 a une longueur axiale de 23.52 mm, j’avoue y perdre mon latin. J’ai déjà lu ce genre de choses sur d’autres sites et je ne comprend pas. Ayant une cataracte et sachant que la longueur axiale a beaucoup d’importance quant à un éventuel décollement de la rétine après opération , celà m’intéresse de savoir pourquoi ces variations. Sachant que j’ai une myopie de -7.00 (od) et -6.50(og), je voudrais savoir à peu près quelle peut être la longueur axiale de mes yeux. Merci beaucoup.
Quel est le pourcentage de décollement de la rétine après opération de la cataracte chez un myope comme moi d’environ 50 ans ?
Merci beaucoup
salut damien !
tu t’es déjà fait tapé au derche ?
bonjour ,
avez vous lu les articles sur la prévention de la myopie à l’aide des cellules souches .Elles permettraient d’empêcher la myopie d’évoluer , et pourquoi si je me trompe de la réduire , ça serait le rêve pour les forts myopes , ou corriger les petites myopies comme -0,5 dont on ne prend pas le risque d’utiliser le laser c’est le cas pour moi.Allez vous étudier cette piste qui pour moi me semble très prometteuse à l’institut de la myopie de 2023? je continue de faire des dons même si c’est moins régulier en ce moment
je vous laisse l’ articles que j’ai pu trouvé:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4878684/
Le problème c ‘est que je me demande comment injecter les cellules souches mesenchymales et autres dans la face postérieur de l’oeil pour augmenter l’épaisseur de la sclère et espérer raccouricir la longueur axiale ,et comment faire en sorte qu’elles ne soient pas éliminer par le système immunitaire lors de l’implantation?
Cordialement
Il est possible que cette différence de taille d’image (anéisoconie) soit liée à la différence de correction entre l’oeil droit et l’oeil gauche. Les verres de lunettes qui corrigent la myopie procurent une réduction de la taille apparente des objets (ceci est lié à des phénomènes optiques, qui induisent une réduction de la taille de l’image rétinien). Un test en lentilles de contact permettrait de lever ce doute, car les effets de réduction de la taille des images sont moindre quand la correction est dans le plan cornéen (ceci explique pourquoi les myopes voient mieux avec des lentilles: l’image rétinienne est plus grande qu’en lunettes, et donc est mieux échantillonnée par les photorécepteurs rétinien de la fovéa).
Bonjour
Je suis myope et astygmate(OD -8 -2.5 OG -6.5 -3.5)
J ai remarqué qu’avec ou sans lunette la taille des objets est significativement différente d un oeil a l autre
Quand je ferme l oeil droit les objets sont plus petits
Et quand je ferme l oeil gauche les objets sont plus grands .A quoi cette différence de perception de taille serait due ?
Merci par avance de votre aide
Cordialement
La différence de correction est minime, et la correction est elle- même assez minime; la différence d’axe pour l’astigmatisme est difficile à interpréter, mais dans tous les cas, il n’y a pas de progression avérée et le changement d’axe ne devrait pas produire de changement majeur pour cette magnitude d’astigmatisme.
Bonjour, Je viens de refaire un examen occulaire chez l’ophtalmologiste, pour vérifier si ma myopie légère ne baissait pas. J’en avais fait un il y a 5 ans, et c’est la que j’avais découvert que j’étais légerement myope. Le résulat d’après cet ophtalmo est qu’elle n’a pas évolué, elle est resté stable pendant ces 5 ans. Mais cet ophtalmo est différent de celui que j’ai vu il y a 5 ans, je suis parti chez un plus près de chez moi. Je lui demande une ordonnance pour pouvoir me payer une autre paire de lunette. Quand je lis l’ordonnance pour les vers correcteur, les résultats ne sont pas les même que sur mon ancienne ordonnance en particulier pour l’oeil gauche. Je vous montre l’exemple ci contre : Ancienne Ordonnance : Oeil droit : -0.50 Oeil gauche : (145° -0.25) -0.25 Nouvelle Ordonnance Oeil droit: -0.50 Oeil gauche: -0.25 (-0.25) 95° Je ne sais pas pourquoi les résultat en dégres des axes ont changé,qu’est-ce que cela signifie ? Est-ce que c’est la même valeur mais écrite différemment selon les ophtalmo, ou bien il y a une légère correction à faire sur mes lunette ? Je ne sais si ça va changer quelque chose au niveau de la correction si j’achète des lunette avec cette nouvelle ordonnance, j’appréhende le fait que cette ordonnance corrige mal mes nouvelles lunettes et par conséquent ma vue ? Pensez-vous que je devrais plutôt retourner chez l’ophtalmo qui m’a fait cette ancienne ordonnance et refaire un examen ? Est-ce que les résultat des axes seront les mêmes ? Doit-je en parler avec mon opticien ? Cordialement