Pouvoir optique paraxial du cristallin
Calcul de la puissance optique paraxiale (vergence) du cristallin
Le pouvoir optique paraxial ou vergence du cristallin dépend de la courbure de ses faces avant et arrière, de son indice, ainsi que de son épaisseur. Le cristallin est une structure élastique et souple (ceci permet l’accommodation, jusqu’à l’installation de la presbytie). Il possède un indice qui varie entre le centre (noyau) et la périphérie (cortex). A l’avant, sa face antérieure est au contact de l’humeur aqueuse, à l’arrière, au contact du vitré.
Les calculs suivants seront effectués sur des valeurs numériques utilisées par le modèle simplifié d’œil théorique de Le Grand. La face antérieure du cristallin est la 3e interface que la lumière rencontre au cours de son trajet intra-oculaire; la face postérieure la 4e.
Dans ce modèle :
-le rayon de courbure de la face antérieure est R3 est de 10.2 mm
– le rayon de courbure de la face postérieure R4 est de -6 mm
-l’épaisseur du cristallin est de ecr=4mm
-l’indice de réfraction du cristallin est ncr=1.42
-l’indice de réfraction de l’humeur aqueuse est nhaq=1.337
-l’indice de réfraction du vitré est nvit=1.3360

Représentation des constantes anatomiques et physiques permettant de calculer la puissance paraxiale du cristallin
Détermination de la puissance de la face avant du cristallin
La puissance de la face avant du cristallin D3 est donnée par
D3 = (ncr – nhaq)/ R3 = (1.42 – 1.337)/0.0102 = 8.14 D
Distances focales de la face avant
On peut dorénavant calculer la distance focale objet et image car on connait les indices de réfraction des milieux que sépare le dioptre représenté par la face avant du cristallin (humeur aqueuse et cortex du cristallin).
La distance focale objet est f3= -1.337 / 8.14 =- 0.16425 m
La distance focale image est f’3= 1.42 / 8.14 = 0.17445 m
Détermination de la puissance de la face arrière du cristallin
Le dioptre constitué par la face arrière du cristallin sépare le cortex postérieur du vitré.
D4 = (nvit – ncr)/ R4 = (1.36 – 1.42)/-0.006 = 14 D
Distances focales de la face arrière
La distance focale objet est f4= -1.42/14 =- 0.10143 m
La distance focale image est f’4= 1.337 / 14 =0.0955 m
Détermination de la puissance d’un système centré équivalent au cristallin
On utilise la formule de Gullstrand, qui prend en compte la distance entre les vertex des surfaces réfractives (soit l’épaisseur du cristallin). Elle permet de calculer la puissance du système global (Dcr), constitué de la face avant et arrière du cristallin
Dcr = D3 + D4 – ecr x (D3x D4)/ ncr = 8.14 + 14 – 0.004 x 8.14×14/1.42 = 21.82 D
Distances focales du cristallin entier
Attention, ces distances sont repérées vis à vis des positions respectives des plans principaux objet et image du cristallin (qui seront déterminées plus bas)
La distance focale objet est donnée par :
fcr= -1.337/ Dcr=-1.337/21.82 = – 0.06127 m
La distance focale image est donnée par :
f’cr= 1.42/ Dcr=1.42/21.82 = 0.06123 m
Il reste maintenant à déterminer la position des plans principaux du cristallin, et tous les éléments nécessaires à ce calcul sont disponibles.
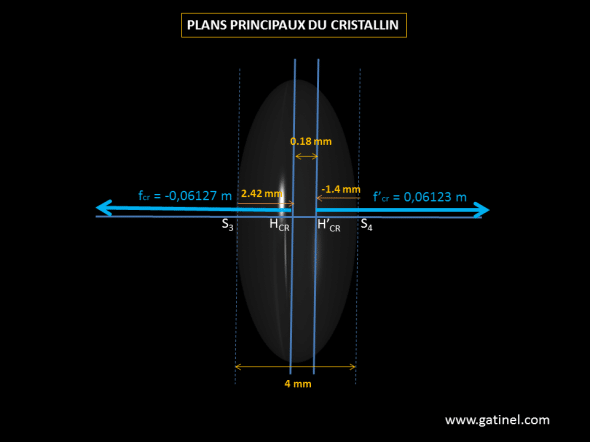
Détermination des plans principaux du cristallin
(voir au besoin pour plus d’explications de fond les pages consacrées à l’optique paraxiale et les plans principaux, et la page consacrée aux plans et points principaux d’un système optique paraxial)
Plan principal objet :
La distance avec le sommet de la face antérieure du cristallin est donnée par :
S3Hcr= ecr x fcr / f4 = 4 x -61.23 / -101.43 = 2.42 mm
Plan principal image:
La distance avec le sommet de la face postérieure du cristallin est donnée par :
S4H’cr= ecr x fcr / f3 = 4 x -61.27 / 174.45 = -1.4 mm
Conclusion
La puissance optique du cristallin (vergence) non accommodant est proche de 22D (dans l’oeil). Le calcul biométrique, qui vise à calculer la puissance d’un implant destiné à remplacer le cristallin, fournit généralement une valeur moyenne proche de 22D dans la population des yeux candidats à une opération de la cataracte.
Il est probable que la puissance du cristallin naturel non accommodé varie moins d’un oeil à l’autre que la puissance de la cornée. Ceci est lié au fait que la différence d’indice entre le cristallin et les milieux dans lesquels il baigne est environ 4 fois moins prononcée que pour la cornée, qui est au contact de l’air (différence d’indice air/cornée = 0.376, différence d’indice cristallin humeur aqueuse =0.09). La déformation du cristallin lors de l’accommodation (réduction du rayon de courbure antérieure), est toutefois à même de fournir une augmentation notable de sa puissance. Par exemple, en utilisant le même modèle de cristallin dont la courbure antérieure serait dorénavant de 7 mm (et l’épaisseur, accrue en raison de la forme plus sphérique du cristallin, de 5 mm, on ne modifie pas la géométrie de la face postérieure), on obtient une puissance accrue d’environ 5 dioptries.
Le but du calcul biométrique n’est pas de calculer la puissance du cristallin « in situ » pour le remplacer par un implant de même puissance, mais prédire quelle valeur devra avoir l’implant de remplacement pour permettre à l’oeil d’obtenir la vision (réfraction) souhaitée. Chez les myopes forts, le remplacement du cristallin naturel par un cristallin artificiel moins puissant (ex: 10D) permet de corriger partiellement ou totalement la myopie. Chez les hypermétropes, le cristallin artificiel possède une puissance supérieure à 22 D (entre 23D et 34 D selon l’importance de l’emmétropie): ce surcroit de puissance permet de pallier la plus faible distance focale imposée pour l’emmétropie par une longueur axiale de l’oeil inférieure à la moyenne.
Le calcul biométrique repose sur des mesures précises qui prennent en compte la puissance optique de la cornée, la longueur axiale, et d’autres paramètres anatomiques, selon la formule de calcul choisie. La position de l’implant dans l’oeil après l’opération ne peut toutefois qu’être prédite, et ceci introduit une certaine « marge d’erreur » dans le calcul biométrique. En fonction de la géométrie de l’implant, du sac capsulaire etc., une incertitude d’environ 1 mm existe.
La position effective de l’implant correspond à la distance entre le plan principal image de la cornée (voir puissance et plan principaux de la cornée), et le plan principal objet du cristallin artificiel.
La connaissance de ces éléments est indispensable pour le calcul de la puissance optique d’un modèle d’oeil entier.

Laisser un commentaire