12. Refraction of the pseudophakic eye
This page is devoted to calculating the theoretical refraction in the spectacle plane of a pseudophakic eye when we know the IOL effective position (ELP) and its optical power and the main ocular biometric parameters (anatomical axial length, total corneal power). This allows, particularly, to study the theoretical impact on ocular refraction of biometric variables and those related to the implant (power, design, and effective position). An interactive spreadsheet allows you to play with these parameters at the end of this page.
The refraction of the pseudophakic eye is equal to the power of the corrective lens, which allows the light emitted by a distant point source to be focused in the retinal plane after passing through the spectacle lens and the ocular media.
A page is dedicated to elaborating an IOL power calculation formula intended to induce the refraction R (R=0 when targeting emmetropia) in the air (n0=1) for an eye of known axial length and total corneal power.
In the present case, it is a question of predicting the refraction of an eye of which we know the biometric dimensions, the power, and the effective position of the IOL.
We will use a simple method, which calculates the total theoretical corneal power allowing to induce emmetropia. The eye’s refraction is then computed as the difference between this value and the measured corneal power.
One can apply it to an eye model based on thin-lens equations (which ignore the optical effects of lens thicknesses and shape factors) or a specific thick-lens eye model.
We will also present another method, based on the use of the vergence formula.
Calculation of the emmetropizing corneal power
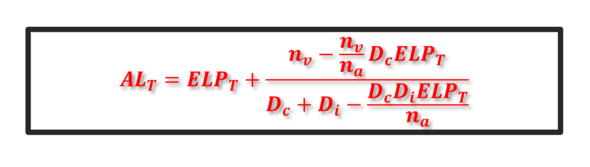
We have established a formula to relate the main biometric dimensions of the emmetropic pseudophakic eye using thick lenses paraxial modeling:
Where:
- ALT is equal to the anatomical axial length of the emmetropic eye (ALA) reduced by the distance between the principal planes of the implant (HiH’i) and the distance between the anterior surface of the cornea and the secondary principal plane of the cornea (S1H’c).
- ELPT is referred to here as the effective lens position of a thick IOL, i.e., the distance separating the principal image plane of the cornea from the principal object plane of the IOL (H’cHi).
- na is the refractive index of the aqueous humor
- nv is the refractive index of the vitreous
- Dc is the total power of the cornea
- Di is the total power of the IOL
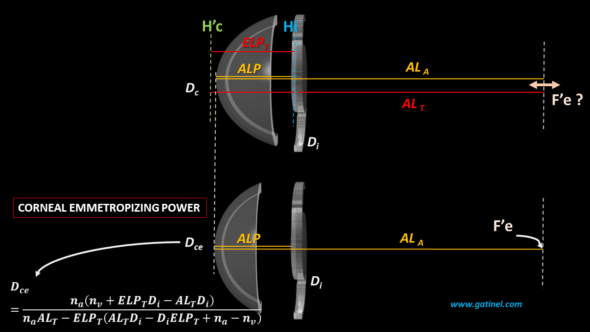
Using the formula above, we can calculate ALT, i.e., the distance separating the principal image plane of the cornea and the theoretical image focus (F’e) of the couple cornea + IOL.
From the value of the ALT and the parameters that describe the curvatures of the anterior and posterior surfaces of the cornea and the IOL, the distances between them, and their respective refractive indices, we can obtain the value of the anatomical length axial ALA (the calculations are detailed on this page). This provides the value corresponding to the axial length making that pseudophakic eye emmetropic. If this distance is shorter than the measured axial length, then the eye is myopic. If it is longer, the eye is hyperopic. And, of course, if it coincides with ALA, the eye is emmetropic!
Rather than comparing these distances, it is more convenient to calculate the value of the total corneal power of the eye considered, which would give it emmetropia. If this value is equal to that of the measured corneal power, then the eye is emmetropic. If it is lower, the eye is myopic, and if it is higher, the eye is hyperopic.
Solving the above equation for Dc provides the expected total corneal power Dce for which the considered eye is emmetropic when an IOL of power Di is positioned so that its object principal plane Hi is located at distance ELPT from the image principal plane H’c of the cornea:
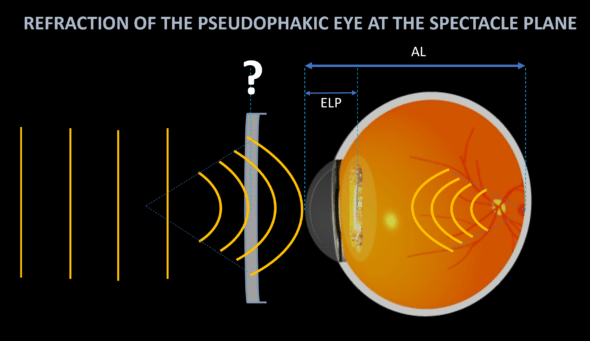
Refraction of the pseudophakic eye in the spectacle plane
The refraction (spherical equivalent, SE) in the spectacle plane of a given pseudophakic eye is a function of the difference between Dc and Dce in the corneal plane:
where d is the distance to the spectacle plane (12 to 15 mm in most cases).
When Dce = Dc, then SE = 0.
When Dce < Dc, this means that the measured power of the studied eye is too high, and consequently, this eye is myopic (SE <0).
Vergence formula to determine an explicit equation for the refraction of the pseudophakic eye
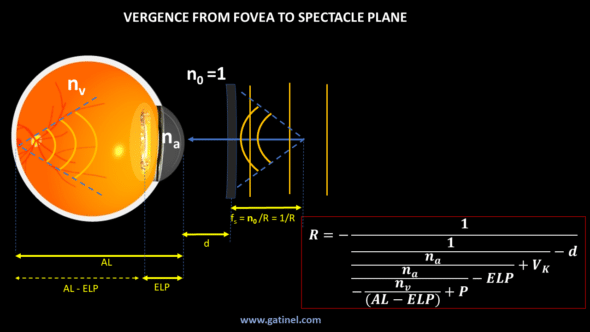
Refraction of the pseudophakic eye (spherical equivalent, in diopters) computed from the iterative use of the vergence formula from the fovea to the spectacle plane. The formula is given for a myopic eye (the vergence of the corrective spectacle glass is negative). The minus sign of the most inferior fraction reflects the divergence of the vergence that emanated from the fovea.
We will not detail all the stages of the calculation as we did on the page dedicated to the calculation of the IOL power. The informed reader will be able to exercise his talents by finding this explicit formula by calculating iteratively using the vergence formula, from the following diagram.
The purpose of the calculation is to determine the refraction R (in diopter) of a pseudophakic eye of corneal power Vk having received an IOL of power P, that is to say, the vergence of a spectacle lens placed at the distance d and of opposite vergence the vergence propagated from the fovea through ocular mediums to d. As the form of the equation suggests, we apply the vergence formula to each interface, and the calculated vergence allows us to determine the distance to the next real or virtual focus (by dividing the refractive index of the medium by this vergence). The vergence exiting the eye is centered on the uncorrected eye’s punctum remotum (PR) which coincides with the spectacle lens image foci to conjugate incoming parallel rays ( » infinite distance ») with the fovea.
Computing the refraction of the pseudophakic eye
The following spreadsheet makes it possible to calculate the theoretical spherical equivalent of a pseudophakic eye.
But, first, we need to enter the biometric parameters (anatomical axial length ALA, corneal radii Rca and Rcp, thickness dc), the power, and the anatomical position of the IOL (ILP: distance between the posterior surface of the cornea and the vertex of the IOL). From the characteristics of the implant (design = X Coddington factor –>curvatures, thickness, refractive index), it is possible to calculate its effective position as a thick lens (related to the position of its principal object plane). ALP is the distance between the anterior surface of the cornea and the vertex of the IOL.
As you will see using this spreadsheet, an isolated variation of the Coddington factor is likely to vary the power of the IOL required to reach the refractive target. We have published a paper focused on this issue.
This strongly suggests that disclosure of IOL radius of curvatures, thicknesses, and refractive indices by IOL manufacturers could be beneficial, especially when dealing with asymmetrical IOLs, both for the development and prediction phases.

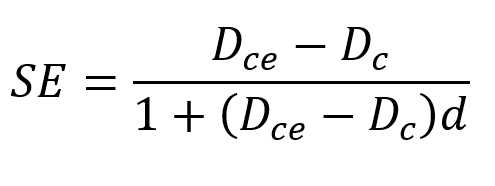
Thank you for your message and scrutinous read. Regarding your question, I would adopt a combined approach, in thick lenses, that takes into account the position of the principal planes, and apply vergence calculation on these.
Cher, Dr. Gatinel
your exposition of pseudophakic optics is tremendous and has helped me a lot.
In your above spreadsheet you subtract instead of add CCT from ILP to calculate ALP. I think by accident.
Besides, I am working on a vergence based calculation method with ELP prediction from personal surgical data and exact IOL data (both toric and non-toric IOL). What is your take on using either principal plane or vergence methods?
Thank you. Best wishes,
Felix
Giessen, Germany