Reflets et images de Purkinje
Etude des reflets oculaires
Ces images, décrites par l’anatomiste tchèque Jan Evangelista Purkinje (19e siècle), sont formées par les réflexions de la lumière incidente sur les surfaces des éléments optiques de l’œil : la cornée et le cristallin. Elles peuvent être utilisées pour étudier la courbure et le décentrement relatif de ces surfaces optiques, ou repérer certains axes comme l’axe optique, et l’axe pupillaire. Le reflet cornéen antérieur est le plus important en clinique.
En effet, l’étude du reflet d’une image sur la cornée permet de calculer sa courbure et d’en déduire sa puissance optique centrale (kératométrie). Le reflet spéculaire d’une image constituée d’un disque de Placido est à la base de la réalisation de l’examen de topographie cornéenne spéculaire.
Leur étude plus approfondies nécessite de connaître quelques lois d’optique géométrique relatives à la réflexion spéculaire sur les surfaces courbes (miroirs convexes et concaves).
Réflexion spéculaire
L’intégralité de la lumière qui pénètre l’œil ne participe pas à la formation de l’image rétinienne ; une partie de celle-ci est diffusée (dispersion lumineuse liées à la transparente imparfaite des tissus oculaires), une autre est absorbée, et enfin – c’est ce qui nous intéresse dans le contexte de l’étude des images de Purkinje, un faible pourcentage de la lumière incidente subit une réflexion. C’est cette faible proportion de la lumière réfléchie qui forme les images des reflets qu’un observateur peut observer.
Le caractère « spéculaire » de cette réflexion est lié au fait que la cornée, recouverte du film lacrymal, est une surface lisse, de même que, dans une moindre mesure, la face arrière de la cornée, les faces antérieure et postérieure du cristallin.
Caractérisation des images de Purkinje
Les images de Purkinje sont induites par des réflexions lumineuses : les surfaces oculaires concernées agissent comme des miroirs. Le nombre d’images de Purkinje est égal à celui (quatre) des surfaces rencontrées par la lumière, qui fournissent chacune un reflet : face antérieure de la cornée, face postérieure de la cornée, face antérieure du cristallin, face postérieure du cristallin. Les images obtenues par ces réflexions successives sont appelées : PI, PII, PIII, PIV. L’image la plus facile à observer est PI, car l’éclat de ce reflet cornéen domine largement celui des trois autres images. Dans certaines circonstances cliniques, on peut également observer PIV (après chirurgie de la cataracte, grâce au reflet induit par la face postérieure du cristallin artificiel).
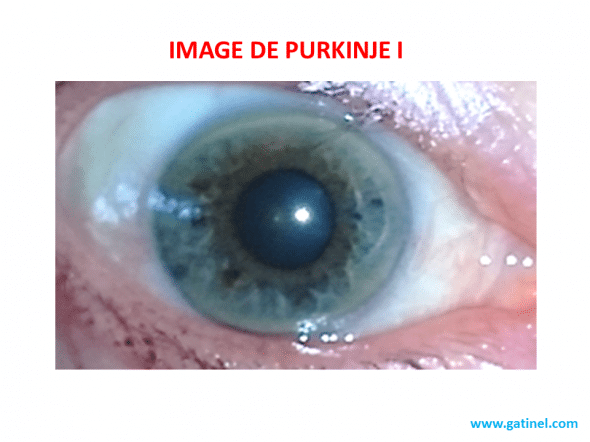
Exemple de l’image de Purkinje I, plus communément appelée « reflet cornéen ». L’intensité du flash utilisé pour prendre ce cliché et obtenir le reflet cornéen permet également d’observer l’éclat de l’image Purkinje IV(liée à la réflexion de la surface postérieure du cristallin). On note la localisation nasale du reflet cornéen (Purkinje I) : elle traduit le décentrement relatif de la cornée vis à vis de l’axe optique (médian) de l’oeil.
Si le reflet cornéen est superposé avec le centre géométrique de la pupille, il matérialise alors l‘axe pupillaire. En général, et particulièrement chez les hypermétropes et astigmates, le reflet cornéen se projette en nasal de l’aire pupillaire. L’écart entre l’axe visuel (qui perfore le dôme cornéen dans une région supposée proche du vertex) et l’axe pupillaire est quantifié comme un angle: l’angle kappa.
En topographie cornéenne, le reflet spéculaire du centre de la mire de fixation (l’anneau central du disque de Placido) permet de localiser l’axe kératométrique, qui relie ce reflet à la mire, et contient le centre de courbure local de la cornée.
Pour une même source lumineuse incidente, située à une distance donnée de l’œil:
L’intensité de ces quatre images de Purkinje dépend de la différence d’indice entre le milieu incident et le milieu réfléchissant.
Leur taille dépend de la courbure de la surface réfléchissante
Leur position dépend également de la courbure des surfaces réfléchissantes.
L’accommodation cristallinienne modifie la courbure des faces antérieures et postérieures du cristallin ; lors de l’accommodation, on observe logiquement une variation de la position de PIII et PIV.
La figure suivante représente schématiquement la localisation axiale des plans où se forment ces images de Purkinje.
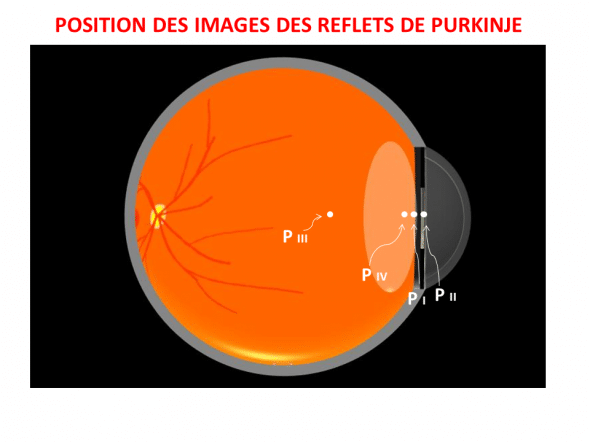
Le calcul plus ou moins complexe selon l’image concernée permet de localiser le plan où se forment ces images en réflexion. PI et PIV sont situées dans des plans assez proches. PII,très difficile à observer, se situe dans un plan très légèrement antérieur à PI. On peut observer PIII avec une intensité source importante, et une focalisation de l’optique de la caméra de visualisation non loin de son plan, qui est plus postérieur que pour les autres images. PIV est difficile à observer avec les moyens courants dans des yeux phakes (cristallin naturel), mais le reflet PIV d’un implant de cristallin artificiel est plus aisée à observer sous le microscope opératoire.
Intensité des images de Purkinje
L’intensité (l’éclat apparent) de l’image obtenue en réflexion dépend de la proportion de la lumière réfléchie (R) vis-à-vis de la lumière transmise (T) : elle est donnée par les équations de Fresnel :
R = (n’ – n)2 / (n’ + n) ^2 où n est l’indice de réfraction du milieu incident et n’ celui du milieu réfléchissant (ex : n = 1 pour l’air et n = 1.336 : film lacrymal / pour l’image PI).
Avec R + T = 1 , et de fait T = 4nn’/ (n’ + n)2
Ces équations négligent la possibilité d’une absorption lumineuse par les structures traversées.
L’intensité R est donc d’autant plus importante que la différence d’indice est grande. Ainsi, l’éclat de PI est environ 100 fois supérieur à celui des autres images, car la différence d’indice entre le stroma et l’humeur aqueuse cristallin et vitré est beaucoup plus faible.
Une source lumineuse de 1 candéls (éclat apparent proche de celui d’une bougie) fournira en réflexion cornéenne (PI) une image dont l’éclat sera égal à :
I = 1 x (0.336)2/ x (1.336)2 = 0.063 candela.
La surface antérieure de la cornée réfléchit environ 6% de l’intensité de la lumière incidente.
En utilisant les valeurs d’indice de réfraction des milieux oculaires, on peut calculer que vis-à-vis de de PI, l’éclat relatif de PII est de ≈ 0.009%, PIII = 0.01%, et PIV = 0.01%.
Taille et position axiale des images de Purkinje
La position d’une image de Purkinje correspond à la position « apparente » de l’image formée en réflexion par une surface. Le cas de figure le plus simple est celui de la première image de Purkinje (PI), car elle est le fruit de la réflexion des rayons lumineux sans qu’ils aient subi de réfraction préalable.
Le calcul de la taille et de la position des images suivantes est plus complexe, car il convient alors de prendre en compte l’effet de la réfraction des dioptres précédent la réflexion.
L’observation du reflet cornéen tend à induire la perception intuitive que cette image se forme « sur » le dôme cornéen. La position de l’image doit être comprise ici comme la position « apparente » de l’image réfléchie, qui correspond à la position qu’occupe virtuellement dans l’espace le plan où se situent les points de l’image formée par la réflexion des rayons incidents issus des points sources sur un miroir convexe (la surface de la cornée). Dans le cas d’un miroir convexe, pour une source lointaine située proche de l’axe optique, l’image en réflexion se forme dans un plan qui situé derrière la surface du miroir (et donc « dans l’œil », derrière la cornée).
Un calcul utilisant la formule de conjugaison, assimilant la cornée à un miroir sphérique convexe dont le rayon de courbure apical serait de 8 mm permet de calculer que la position de l’image PI d’une source située à l’infini est à 4 mm du sommet cornéen (le foyer du miroir est situé à une distance égale à la moitié du rayon de courbure vis à vis du sommet). Si cette source est approchée à 40 cm, l’image apparente se déplace légèrement en avant du foyer (vers le sommet cornéen).
L’image suivante a été obtenue en réalisant une macrophotographie de l’oeil d’un sujet situé à proximité d’une fenêtre. Où se situent le plan de l’image formée par le reflet sur la cornée vis à vis du sommet cornéen, et quelle est sa hauteur?

Réflexion par le film lacrymal d’une cornée humaine : à droite, l’embrasure de la fenêtre fixée par le sujet au moment du cliché. La hauteur de la vitre est égale à 0.6 mètre, et elle est située à 8 mètres du sommet cornéen dont le rayon est de 8mm. La formule de conjugaison permet de calculer la position de l’image en réflexion (située à environ 4 mm en arrière du sommet de la cornée) et sa hauteur: proche de 3 mm.
Dans ce calcul, nous utilisons la formule de conjugaison des miroirs, qui ne s’applique en principe que dans des conditions paraxiales (ce qui en toute rigueur n’est pas le cas ici), et pour plus de commodité et malgré l’absence de réfraction véritable, l’inverse des distances avec le sommet du miroir considéré sera appelé « vergence ».
La hauteur de la fenêtre est de 60 cm, elle est situé à 8 m de la cornée dont le rayon de courbure apical est de R =8 mm.
La vergence de l’objet st égale à V = 1/-8 m = -0.125 D (le signe négatif est lié à la convention qui fait que l’on mesure les distances algébriques en positif vers la droite, négatif vers la gauche). Le foyer du miroir est situé à la moité du rayon de courbure (4 mm en arrière du sommet cornéen). La puissance du miroir est 1/-0.004= 250 D. On déduit la vergence de l’image: -250 D + – 0.125D = -250.125 D. La position de l’image est donnée par l’inverse de la vergence: -1/-250.125 = 0.00399 = 3.99 mm. Cette distance est à droite du sommet cornéen, « dans l’oeil ». La magnification est égale au rapport des vergences objet/image: -0.125 / -250.16 −soit 0.5%. La taille de la fenêtre dans l’image formée est proche de 3 mm.
Qu’en est-il d’une source plus proche, comme celle d’un disque de Placido ?
Imaginons un disque de Placido dont le diamètre total est de 25 cm, situé à 10 cm de la cornée, dont le rayon de courbure apical est de R =7.8 mm.
La vergence du disque V est égale à V = 1/-0.10 m = -10 D (le signe négatif est lié à la convention qui fait que l’on mesure les distances algébriques en positif vers la droite, négatif vers la gauche).
Le foyer du miroir convexe cornéen est situé à ½ R soit 3.9 mm. La vergence correspondante est 1/-0.0039 = -256.4 D. La vergence de l’image Vi est égale à -256.4 + -10 D= -266.4 D. La position de l’image réfléchie vis-à-vis du sommet est de – 1/-266.4 = 0.0037 m = 3.7 mm.
La magnification de l’image est égale au rapport des vergences entre objet et image, soit -10/-266.4=+0.0375 soit environ 4%.
L’image du disque de Placido aura une taille apparente proche de 25 cm x 0.0375 = 0.9375 cm : ceci permet de « couvrir » la quasi intégralité de la surface cornéenne (dont le diamètre est proche de 1cm). La dimension des coupoles de Placido et la distance à laquelle elles doivent être positionnées vis-à-vis de la focale de la caméra numérique qui en photographie le reflet sont respectivement proches de 25 m et 10 cm avec la plupart des systèmes topographiques spéculaires.
Les reflets de Purkinje II et III ont une importance relative en clinique. Le reflet II est très difficile à observer (faible écart d’indice de réfraction entre endothélium et humeur aqueuse). Le reflet III est également ténu, et il se forme dans un plan relativement postérieur. Si l’on observe les reflets de l’oeil de manière coaxiale avec une source lumineuse ponctuelle, on peut définir l’axe optique comme celui qui minimise la distance entre les reflets PI, PII, PIII et PIV.
Le reflet IV est intéressant car issu de la réflexion sur une surface concave (la face postérieure du cristallin); son image se forme dans un plan assez proche de celui du reflet cornéen (Purkinje I). Cependant, il est également très difficile à observer dans des conditions standard d’observation, pour un oeil phake.
Calculons sa position théorique approchée. Pour simplifier ce calcul, on considère les rayons incidents sont issus d’une source située à l’infini, et que la réflexion s’effectue comme dans l’air.
Pour calculer le pouvoir du miroir que représente la face arrière du cristallin, il est nécessaire de connaître sa courbure. La mesure de la courbure de la face postérieure du cristallin est assez difficile avec les moyens d’observation conventionnels : ce sont justement certaines réalisées d’après l’étude des tailles d’image de Purkinje IV qui permettent d’estimer ce rayon (ex : Rabbets in Bennett and Rabbets’ Clinical Visual Optics, 3rd edition, Butterworth –Heinemann). Une valeur de 6 mm peut être considérée comme réaliste pour un cristallin non accommodant (la face antérieure du cristallin est plus plate, son rayon estimé proche de 10 mm – hors accommodation).
Le foyer du miroir cristallinien postérieur est situé à -3 mm du pôle postérieur du cristallin. La puissance du miroir considéré est de +333.33 D. Pour des rayons incidents parallèles, l’image de la réflexion avec la face postérieure du cristallin se forme donc 3 mm en avant du sommet de celle-ci, dans un plan voisin de l’image de Purkinje I, qui elle apparaît environ 3.8 mm en arrière du dôme cornéen. En effet, la distance entre le vertex cornéen et le pôle postérieur du cristallin est proche de 7 mm. Fait notable, cette image PIV est inversée (la puissance est positive), et de fait le coefficient de magnification est négatif.
Dans un oeil modèle de Gullstrand, les distances de chacune des images de Purkinje avec le vertex cornéen sont (Atchinson DA, Smith G, Optics of the human eye, Butterworh Heinemann, 2000) :
PI : 3.850 mm
PII : 3.765 mm
PIII : 10.620 mm
PIV : 3.979 mm
En clinique, l’observation d’un reflet IV s’observe plus facilement dans les yeux pseudophakes, opérés de cataracte, car il existe une différence d’indice de réfraction entre l’implant et le vitré nettement supérieure à celle qui sépare le cortex cristallinien du vitré, et la transparence des milieux oculaires est accrue. Le rayon de courbure des implants est notablement plus grand que celui du cristallin postérieur (proche de 12 mm, en fonction de la puissance et de la géométrie de l’implant). Ceci rapproche encore les images PI et PIV sur le plan axial, cette dernière pouvant alors apparaître dans un plan plus antérieur que l’image PI. Dans un plan frontal, ces images apparaissent non alignées; PI est généralement légèrement décalée en nasal vis à vis du centre géométrique de la cornée. PIV se déplace de manière opposée avec PI, et apparaît en temporal.

L’image de Purkinje IV étant causée par la réflexion avec une surface concave, sont déplacement avec la source se fait à « l’envers » de celui de l’image de Purkinje I, issue de la réflexion sur une surface convexe. Rant et Rpost sont les rayons de courbure « locaux » des surfaces réfléchissantes, considérées comme localement sphériques. Certaines approximations sont effectuées: on considère la source comme suffisamment éloignée pour se placer dans des conditions paraxiales, et des rayons incidents proches de la normale à la surface. Le tracé des rayons permettant de localiser les image utilise les propriétés de deux rayons : celui qui passe par le centre de courbure local n’est pas dévié. Le rayon parallèle (ou quasiment) à la direction de la normale est réfléchi de manière à couper le foyer de la surface réfléchissante (situé à une distance égale à la moitié du rayon vis-à-vis deu sommet de la surface considérée). Dans cet exemple (cristallin artificiel), le rayon de courbure de l’implant (représenté en rouge, en général compris entre 10 et 12 mm) est plus grand que le rayon de courbure de la cornée antérieure (proche de 8 mm). Le trajet des rayons proches de l’axe est représenté en vert pour la réflexion sur la face postérieure de l’implant, et en orange pour la réflexion sur la cornée (les rayons coïncidents avec la normale à la surface considérée sont en bleu).
Pour le chirurgien éclairé, cette image est bien visible lors de la chirurgie de la cataracte, une fois l’implant posé ; elle est brillante car issue de la réflexion des ampoules d’éclairages coaxiales au système de visée microscopique opératoire, et se déplace en opposition avec PI lors des mouvements oculaires.

L’image de Purkinje I (ou reflet cornéen) correspond ici à celle des sources lumineuses du système d’illumination du champ opératoire (microscope Zeiss). La face postérieure du cristallin artificiel (ici un implant Physiol Finevision trifocal) est à l’origine d’un reflet un peu moins brillant, inversé, et dont le déplacement se fait en opposition avec celui du reflet cornéen lors des mouvements oculaires.
Après chirurgie de la cataracte, le quatrième reflet de Purkinje (face postérieure de l’implant) est également visible. L’image suivante permet d ‘observer une image en coupe horizontale de l’oeil gauche après chirurgie de la cataracte et pose d’un implant diffractif trifocal. En raison de la présence d’un angle Kappa relativement prononcé, la rotation externe de l’oeil fixant le centre de la mire coxiale de kératométrie du biomètre IOL Master 700 provoque un déplacement nasal de l’image I de Purkinke (vertex) et temporal de l’image IV de Purkinje (face postérieure de l’implant).

Cliché en lumière visible du segment antérieur (en bas) et coupe OCT (lumière infrarouge) en haut, révélant l’angulation des structures du segment antérieur vis à vis de l’axe optique de l’oeil (l’angle kappa, entre l’axe pupillaire et l’axe visuel est particulièrement prononcé). Notez le « tilt » apparent de l’implant vis à vis de l’axe visuel.

Bonsoir Monsieur Gatinel, Comment peut on savoir si le reflet P1 est bien celui de l’oeil d’une personne vivante.
L’angle Lambda est défini comme l’angle formé par l’axe pupillaire et la ligne de visée (line of sight). Effectivement, les instruments comme l’Orbscan qui fournissent une estimation réelle (angle exprimé en degré) de l’angle kappa donnent en effet plutôt une estimation de l’angle lambda (le repérage de la ligne de visée qui relie le point de fixation et le centre de la pupille est aisément effectué par l’instrument, alors que l’axe visuel demeure une construction théorique paraxiale qui requiert de connaître l’emplacement des points nodaux). En pratique ces angles (kappa et lambda) sont très proches, mais il peut exister des différences sensibles dans le cas ou l’axe visuel forme un angle important avec la ligne de visée. Enfin, la mesure de l’angle kappa (qui correspond implicitement à l’angle lambda en pratique) est souvent assimilée à la distance entre le centre de la pupille et l’image 1 de Purkinje (vertex). Il est vrai que lorsque l’angle lambda augmente, cette flèche augmente aussi, puisque le reflet 1 de Purkinje se déplace (en nasal dans la grande majorité des cas).
Bonjour De Gatinel,
Par rapport a cette affirmation : « L’écart entre l’axe visuel (qui perfore le dôme cornéen dans une région supposée proche du vertex) et l’axe pupillaire est quantifié comme un angle: l’angle kappa. ». Ne serait-ce pas plutôt l’angle lambda, qui serait par ailleurs le seul angle mesurable cliniquement ? (Cf. « les strabismes » de Annette Spielmann, p.37).
Merci en tous cas pour vos explications qui m’ont été d’une grande aide pour la compréhension de ces principes.
Cordialement,
Nathan
Non, je n’ai pas connaissance d’une telle méthode!
Bonjour Dr Gatinel,
Je vous remercie pour l’explication des images de Purkinje.
Connaissez-vous une méthode qui permettrait de mesurer l’absorption spectrale des 4 images de Purkinje ?
Cordialement
Jade