Formule de vergence
La formule de vergence
La formule de vergence est très utile en ophtalmologie. Elle sert à calculer la position où se forme l’image d’un objet après réfraction de la lumière par un système optique: ce système peut être simple (une lentille mince) ou complexe (le couple cornée + cristallin).
La vergence – ou puissance optique paraxiale – s’exprime en dioptrie. Pour une surface optique, elle est égale à l’inverse de la distance qui sépare du sommet du système optique du plan ou se forme l’image nette (plus précisément du plan principal image au foyer image en optique paraxiale) multipliée par l’indice de réfraction du milieu considéré.
L’utilisation de la formule de vergence permet de faire divers calculs sans avoir besoin de calculer le trajet de nombreux rayons au travers du système optique. Elle permet notamment d’établir une formule simple pour le calcul de la puissance de l’implant posé au cours de la chirurgie de la cataracte. Elle permet aussi d’établir les formules visant à convertir la puissance d’un verre de lunette à partir d’une puissance de lentille (et vice versa) en fonction de la distance verre oeil.
La vergence de l’œil découle de la somme de la vergence de la cornée et de la vergence du cristallin. Au cours de l’accommodation, la vergence du cristallin augmente (le cristallin se déforme et adopte une courbure plus importante).
La formule de vergence fait intervenir la position de l’objet source, sa distance avec le système optique dans un milieu d’indice de réfraction donné et la vergence, ou puissance optique de ce système.
Cette page est consacrée à la formule de vergence: son origine est rapportée, et ses quelques applications mentionnées.
Origine de la formule de vergence
La formule de vergence peut être établie à partir de la loi établissant le trajet après réfraction des rayons lumineux: loi de Snell (ou Snell-Descartes) , appliquée dans des conditions paraxiales. Elle découle de certaines approximations que l’on peut faire dans ces conditions, où l’on considère la partie du système optique proche de l’axe optique, (conditions paraxiales) et où les rayons forment un angle faible avec cet axe. La formule de vergence permet de calculer la position de l’image d’une source sans avoir besoin d’utiliser un calcul de lancer de rayons (ray tracing).
Prenons l’exemple d’un système optique simple, et d’un objet source (S) situé très loin de celui-ci, à l’infini:
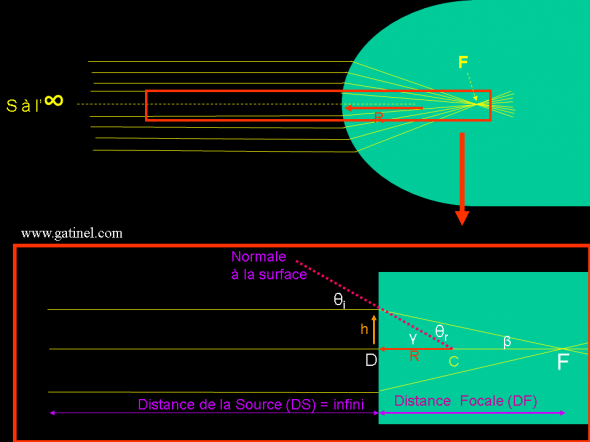
Un système optique considéré dans les conditions paraxiales peut être approché comme « plat » dans la région très proche de l’axe optique. Ceci permet de réaliser des approximations géométriques utiles pour le calcul du tracé des rayons réfractés par le système. Dans le cas présenté, les rayons sont parallèles à l’axe optique, et dans les conditions paraxiales, nous verrons que ces rayons sont focalisés vers le foyer du système (qu’il ne faut pas confondre avec le centre de courbure C). θi et θt sont les angles d’incidence et de transmission du rayon considéré: ils sont définis par rapport à la « normale » au point d’incidence. Sur le schéma, en raison de l’approximation faite (la surface est plate), la normale n’apparait pas perpendiculaire à la surface: pour de petits angles, la différence est négligeable.
Considérons un cas général, où la source est située non pas à l’infini, mais à une distance O, et baigne dans un milieu d’indice n. Le système optique est un dioptre sphérique de rayon R et d’indice n’. On connait n, n’, O (la distance de la source au dioptre) et R, le rayon de courbure du sommet du dioptre.
La question que peut résoudre la formule de vergence est : où se forme l’image I ?
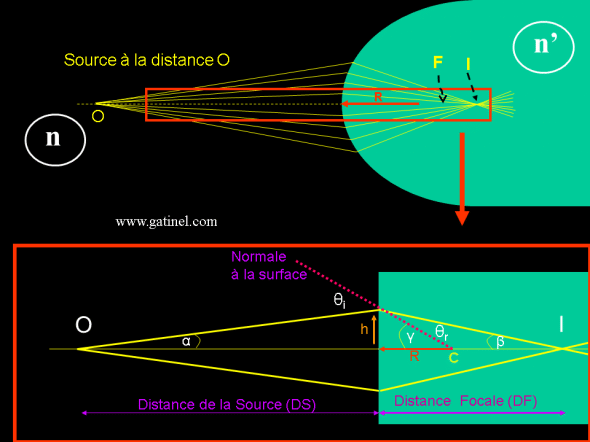
La source est maintenant placée à une distance finie O. Dans les conditions paraxiales, les rayons sont réfractés et se coupent en un point en I, qui est l’image du point O. I est situé en arrière de F, qui est la distance focale du système (mais dont nous n’avons pas besoin à ce stade: la loi de Snell suffit !).
La loi de Snell permet d’écrire : n sin θi = n’ sin θr
Dans les conditions paraxiales, on peut remplacer sin θi par la valeur θi en radians. L’équation devient donc :
n θi = n’ θr
Il faut maintenant exprimer θi et sin θr en fonction de variables plus faciles à mesurer : (rappelons que l’on connait la position de O, la valeur de R, n et n’).
En observant la figure, on peut poser : θi =α +γ
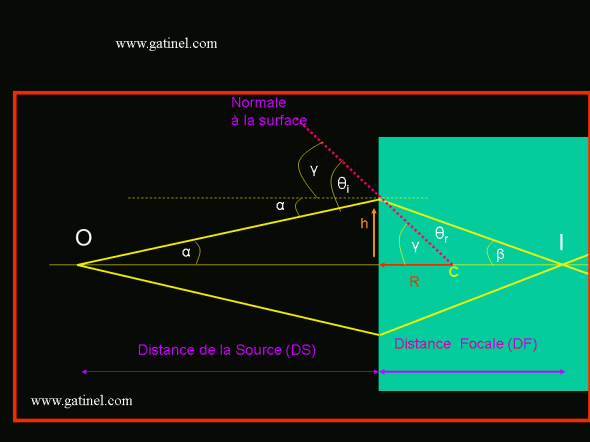
La figure suivante permet d’exprimer l’angle d’incidence θi comme la somme de l’angle du rayon avec l’axe optique α et l’angle entre le segment reliant le point d’entrée et le centre de courbure et l’axe optique γ .
De même, il est possible de vérifier que θr = γ – β
On peut alors remplacer θi =α +γ et θr = γ – β dans la formule de Snell pour obtenir :
n (α +γ) = n’ (γ – β)
n α + n γ = n’ γ – n’ β
n α + n’ β = γ (n’ – n’)
On peut exprimer les angles α γ et β en fonction de h, O (la distance entre O et le sommet optique), i, et R (rappelons que l’on connait les valeurs O et R).
Dans les conditions paraxiales (pour de petits angles):
tan α = α = h/-O = – h/O (la distance O est négative par convention; la distance est mesurée vers la gauche)
tan γ = γ = h/R
tan β = β = h/I
A ce stade, il suffit de connaître h pour trouver la valeur de I. Toutefois, on ne connait pas cette valeur. Cependant, si l’on remplace les valeurs des angles par ces rapports on obtient :
n α + n’ β = γ (n’ – n’) -> -n h/O + n’ h/I = h (n’ – n)/R
On reconnait la formule paraxiale : nu + n’u’ = h (n’-n)/R en posant u=h/O et u’= h/I. Pour obtenir ces deux égalités, il a fallu faire une approximation paraxiale sur les petits angles.
On peut simplifier la formule par h et on obtient finalement :
-n/O + n’/I = (n’ – n)/ R
soit
n’/I = n/O + (n’ – n)/R
On peut alors calculer I, puisque l’on s’est « débarrassé » des inconnues (angles, et hauteur d’incidence h).
On apprécie la puissance de cette formule, qui ne nécessite que de connaître la distance O de l’objet source dans le milieu d’indice n avec le dioptre (dont on connait la courbure R et l’indice n’) pour calculer simplement la distance I de l’image!
Le terme « vergence » provient du fait que chaque terme est proportionnel à l’inverse d’une distance: (n’ – n) / R est la vergence, ou encore puissance réfractive, du dioptre. L’inverse d’une distance (en mètres) s’exprime en dioptries (rappelons que n et n’ sont sans dimension, car ils correspondent au rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans le milieu).
Par exemple, si le dioptre possède un indice de 1.37, et un rayon de courbure R de 8 mm, la vergence du dioptre dans l’air est égale à (1.33 – 1) / 0.008 soit 41.25 Dioptries.
n/O est la vergence de l’objet Vo
n’/I est la vergence de l’image Vi
et (n’ – n) /R est la puissance optique P du dioptre.
On peut ainsi écrire : Vo + P = Vi
Pour calculer ces vergences, il faut tenir compte du signe des distances: négatif vers la gauche, positif vers la droite.
Applications – exemples
Loupe
Sans schéma, cette formule permet de calculer simplement l’endroit ou se forme l’image d’un objet regardé à travers une loupe. Si la loupe à une puissance de 25 D, et que l’on l’approche à 2 cm de l’objet (par exemple un timbre) on peut poser que :
la vergence du timbre + la vergence de la loupe = la vergence de l’image.
La vergence du timbre est de 1/ -0.02 (en mètres) = – 50 D Le signe est négatif si la loupe est à droite du timbre. La vergence de la loupe est 25 D. La vergence de l’image est égale à -50 + 25 = -25 D. Pour obtenir la vergence de l’image, on calcule 1/ -25 = -0.04 mètres = -4 cm. L’image est également à gauche (du même côté que le timbre).
Pour calculer le grandissement (magnification : M), on peut utiliser la formule : M = n x distance image / n x distance objet : (ici n= 1). La magnification est égale au rapport des distance image/objet: l’image apparaît comme un timbre deux fois plus gros et situé à 4 cm derrière la loupe.
Distance verre – œil
La distance verre œil est un paramètre qu’il est important de connaître, notamment pour la conversion entre correction lunettes (verres) et correction en lentilles de contact.
La réfraction d’un œil est souvent exprimée comme la puissance du verre de lunette utilisé pour le corriger. Par exemple, une myopie de -3 D correspond à une amétropie qui est corrigée par la pose d’un verre de -3D. La pose de ce verre est effectuée sur une monture d’essai ou dans un réfracteur automatique: le verre est donc situé à une certaine distance de l’oeil: environ 12 à 15 mm.
La distance du verre avec le foyer image de l’œil n’est pas égale celle du plan principal image de l’œil avec ce foyer image. Pourtant, la réfraction oculaire « vraie » doit être calculée comme l’inverse de la distance entre le plan image et le foyer image, et non entre la distance du verre correcteur et le foyer image.
On peut utiliser les formules de vergence pour prédire la différence entre la réfraction oculaire « vraie » et la réfraction oculaire exprimée dans le plan lunettes. Cette différence, si elle est significative, aura un intérêt pour convertir la réfraction « lunettes » en réfraction « lentilles » : en effet, on peut considérer que le plan cornéen (où est posé la lentille) est confondu avec le plan principal image de l’œil (en réalité situé à 1.5 mm en arrière de la cornée).
Le schéma suivant représente un oeil hypermétrope corrigé par un verre de puissance D (en dioptries).
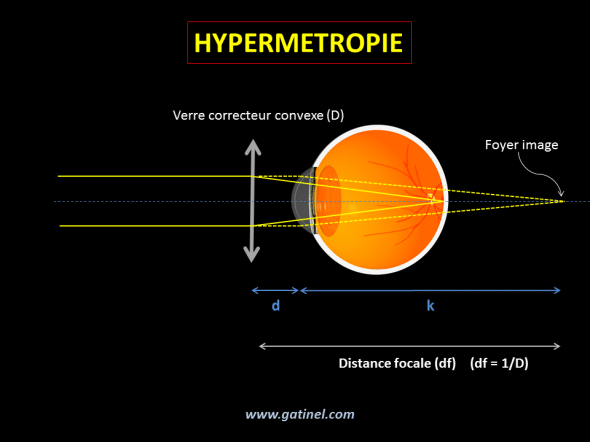
Un hypermétrope corrigé par un verre convexe de puissance positive (ex: +5 D). L’effet du verre est de compenser le défaut de vergence dont est atteint l’œil hypermétrope. Quand le verre est positionné devant l’œil du patient à une distance d, les rayons provenant d’une source lointaine sont focalisés dans le plan de la rétine, et non plus en arrière de celui-ci. Le foyer objet du verre est situé au foyer image de l’œil non corrigé. Le foyer image est situé à la distance k du plan principal image de l’œil (assimilé ici à celui de la cornée).
La vergence de l’oeil est appelée K (en dioptries) : elle est égale à 1/k (k est une distance en mètres). la distance focale du verre est appelée df.
On peut poser k= df -d, d’où K= 1/(df – d). En utilisant l’équation D=1/df on obtient :
K = D /(1 – d x D) : cette formule permet de calculer la réfraction de l’oeil (ou la puissance d’une lentille de contact) à partir de la puissance du verre correcteur (D) et la distance verre-oeil (d>0). Quand d=0, K = D. Quand D est négatif (correction de la myopie); 1- d xD>1 donc K<D. La lentille pour corriger la myopie possède une puissance réduite (en valeur absolue) vis à vis de la correction lunettes.
Sachant que df = k + d, on obtient :
D = K (1+d x K) : cette formule permet de calculer la réfraction du verre de lunette à poser à une distance d quand on connait la réfraction oculaire (ou la puissance de la lentille de contact correctrice).
Quand K est négatif, 1+ dxK <1, et D>K (en valeur absolue)
Exemples :
1) Un oeil hypermétrope est corrigé par une lentille de +5 D. Quelle est la puissance du verre procurant une correction équivalente, sachant que le verre est placé à 13mm de l’oeil?
K = 5D, d’où k=1/5 = 0,2 mètre
La distance focale du verre devra être de 0,2 + 0,013 = 0,213 mètres.
La puissance du verre est égale à 1/0,213 = +4,70 D.
La vergence du verre de lunette est moindre que celle de la lentille.
2) Un oeil myope fort est corrigé par un verre de lunette de -15 D: ce verre est placé sur une monture située à 14 mm de l’œil. Si le patient souhaite une correction en lentille de contact, quelle sera la puissance de celle-ci?
La distance focale du verre est 1/-15 = -0,0667 mètre; le punctum remotum de l’oeil myope est donc situé à 0,00667 + 0,014 = 0,08067 mètres. La lentille doit donc focaliser à : 1/0,08067 = -12,40 dioptries.
La différence de vergence entre le verre et la lentille est importante: -2,50 dioptries environ ! Plus un œil est myope, et plus la différence de vergence entre le verre et la lentille est importante. La lentille est moins puissante que le verre de lunette.
En chirurgie réfractive, la réfraction utilisée pour programmer le laser excimer (LASIK, PKR) est celle de la correction en lunettes ! Lors de la saisie de cette correction, une conversion est effectuée pour calculer la correction effective qui est délivrée dans le plan cornéen.
Dimensions apparentes de la pupille de l’iris
Ce problème est plus complexe… La pupille irienne possède un diamètre anatomique (diamètre physique que l’on mesurerait à l’intérieur de l’œil), qui n’est pas égal à son diamètre apparent: en effet, quand on observe la pupille, on recueille son image virtuelle qui semble située en avant de la pupille anatomique, et dont le diamètre est supérieur au diamètre physique: ceci est du à la « magnification » (grossissement) de l’image de la pupille irienne par le dôme cornéen !
Cette image virtuelle formée par la cornée est la pupille d’entrée de l’œil. Ici, un schéma s’impose :
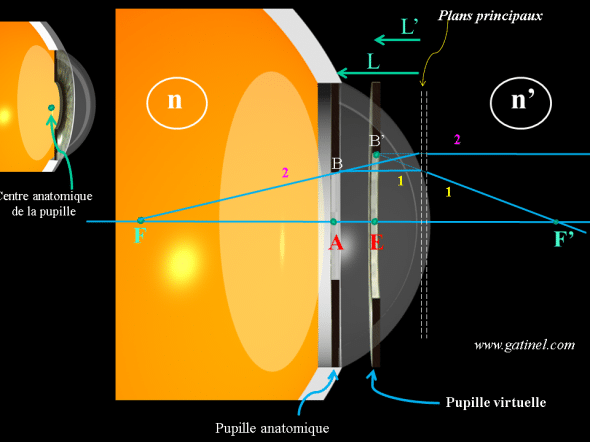
Le rayon de la pupille virtuelle image est EB’, celui de la pupille anatomique est AB. Pour calculer la position apparente de la pupille (position du plan reliant le point E au point B’, correspondant à la distance L’ sur le schéma) on assimile la cornée à un système dont les points cardinaux F et F’ (foyers) et les plans principaux sont connus. Pour une représentation graphique de la position de B’, on peut tracer un rayon (1) qui semble provenir de l’infini (de la gauche) et passe par B en étant parallèle à l’axe optique de la cornée: ce rayon est par définition réfracté vers le foyer F’. Un deuxième rayon est tracé depuis le foyer F: il émerge par définition de la cornée parallèle à l’axe optique. La position de B’ correspond à l’intersection du prolongement des rayons 1 et 2 (en pointillés).
Pour calculer la position du plan de la pupille « virtuelle », on peut utiliser la formule de vergence:
Vergence de la cornée + vergence de l’objet (la pupille) = vergence de l’image formée, soit :
Vergence de la cornée + n/L = n’/L’
On assimile la cornée à un dioptre sphérique, dont l’indice (kératométrique) est proche de celui de l’humeur aqueuse (n = 1.33). La vergence de la cornée est la résultante de la vergence de la face antérieure et de la face postérieure: elle est proche de 43 dioptries en moyenne.
n est l’indice de réfraction de l’humeur aqueuse (1.33). L est la profondeur de la chambre antérieure (3.5 mm soit 0.0035 m) environ (dirigée vers la gauche, L a une valeur négative)
L’indice de réfraction de l’air est 1. La valeur de la position de la pupille virtuelle L’ est égale à : 1 x (-0.0035) / (1.33 -0.0035 x 43) = – 2.97 mm, soit 500 microns en avant du plan de la pupille anatomique.
Pour calculer le grandissement (magnification : M), on peut utiliser la formule : M = n x L’ / n’ x L = 1.33 x 2.97 / 1 x 3.5 = 1.12 : le diamètre apparent de la pupille d’entrée est environ 1.12 fois plus grand que celui de la pupille anatomique. A l’inverse, pour un diamètre apparent de 6 mm, le diamètre réel de la pupille est de 6/1,12 = 5.35 mm.
Les paramètres principaux qui influent sur ce calcul sont la puissance du dioptre cornéen : la magnification est proportionnelle à la vergence cornéenne. Après chirurgie réfractive cornéenne pour la myopie: la vergence est réduite, ce qui peut en théorie provoquer une légère réduction du diamètre apparent de la pupille. En ce qui concerne justement le diamètre de la zone optique à programmer pour la correction de la myopie, il faut tenir compte du diamètre de la pupille d’entrée (c’est-à-dire le diamètre apparent), ainsi que la profondeur de la chambre antérieure. D’autres facteurs sont susceptibles de jouer un rôle quoique minime : l’asphéricité de la cornée, ainsi que la distorsion optique en « barillet » induite par la cornée (qui tend à induire une réduction du diamètre apparent de la pupille).
La formule vergence permet enfin (et surtout) d’établir la formule théorique « mère » du calcul d’implant en chirurgie de la cataracte, qui fait l’objet d’une page spécifique sur le site accessible directement par le lien

C’est très intéressant
Très édifiant et complet merci professeur.