Loi de Snell ou Snell-Descartes
La loi de Snell (Snell Descartes en France) permet de calculer la direction d’un rayon lumineux incident puis réfracté par un milieu optique, si l’on connaît l’indice de réfraction des milieux traversés, et l’angle du rayon incident avec la normale (perpendiculaire) à la surface au point rencontré par le rayon.
Dans le schéma suivant, un rayon incident issu d’un milieu d’indice de réfraction ni rencontre un milieu d’indice de réfraction nr
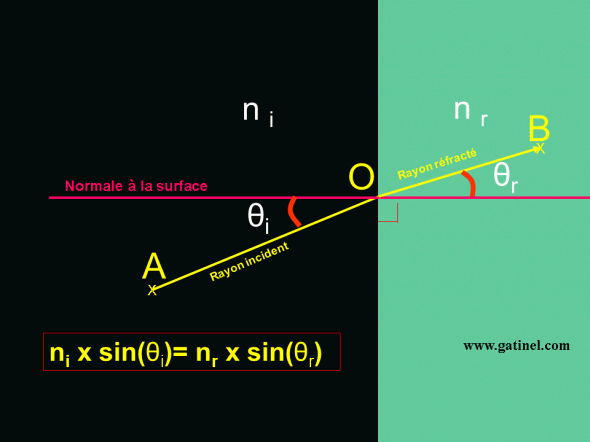
La loi de Snell stipule que l’on peut calculer la direction du rayon réfracté en fonction de celle du rayon incident. Il suffit de connaitre l’indice de réfraction de chaque milieu (ni pour le milieu incident, nr pour le milieu réfractant). Les angles sont établis par rapport à la droite perpendiculaire à la surface du milieu rencontré, au point d’incidence O, cette droite est dénommée droite “normale à la surface”. La loi de Snell s’écrit simplement : ni x sin(i)= nr x sin(r)
La loi de Snell s’écrit simplement : ni x sin(i)= nr x sin(r) où i et r sont respectivement les angles d’incidence et de réfraction (en radian). Dans des conditions paraxiales, on peut poser i=sin(i) et r=sin(r).
Cette loi de Snell peut être démontrée en utilisant le principe de Huygens, en se fondant sur les propriétés de déplacement de proche en proche des ondes lumineuses (voir principe de Huygens et loi de Snell)
Dans des conditions paraxiales, la valeur d’un angle en radian est proche de celle de son sinus (ou de sa tangente).
La loi de Snell devient alors: n i = n’ r avec (i est l’angle d’incidence, r est l’angle de réfraction). Cette approximation conduit au calcul de la formule de vergence.

Sincères félicitations pour cet excellent article.
Il veut s’inscrire
Super bien
Comment démontrer que la tangente de l’angle d’incidence est égale au rapport des indices de réfraction de 2 milieux (n2/n1) svp .merci
Pour cela il faut connaître l’angle de la réfraction avec la surface concernée et résoudre l’équation pour l’angle d’incidence. Il est nécessaire de connaître l’un pour déterminer l’autre.
Bonjour je me demande comment calculer la valeur de l’angle d’incidence sans le mesurer merci d’avance cordialement