Les formules de calcul de puissance d’implant
Les formules qui permettent le calcul de la puissance de l’implant nécessitent préalablement le recueil de données propres à l’oeil opéré. La biométrie oculaire permet le recueil des paramètres nécessaires au calcul de la puissance de l’implant à même d’induire la réfraction désirée après l’opération de la cataracte. La chirurgie de la cataracte consiste au remplacement du cristallin opacifié par un implant de cristallin artificiel; cet implant permet de corriger l’oeil pour une distance de vision nette sans lunettes (ex : la puissance est calculée pour l’emmétropie: vision nette de loin sans lunettes).
Si l’on n’insérait pas un implant en remplacement du cristallin, la plupart des yeux opérés (tous sauf certains yeux très myopes) auraient besoin d’une correction optique pour pallier une hypermétropie induite (la cornée n’a pas la puissance optique suffisant pour focaliser les rayons lumineux incidents sur la rétine).
L’obtention de cette puissance optimale, destinée à induire la correction optique souhaitée par le patient, dépend d’une formule de calcul.
Le lecteur intéressé par les aspects plus fondamentaux concernant ce domaine est invité à consulter les pages (en anglais) de la rubrique https://www.gatinel.com/paraxial-optics-for-iol-power-calculation/
Il existe plusieurs formules de calcul biométrique, non seulement pour des raisons historiques, mais aussi parce que toutes les formules de calcul biométrique reposent sur certaines assomptions (par exemple, la prédiction de la position effective de l’implant, mais aussi l’indice de réfraction de la cornée et des autres milieux oculaires, etc.). Ces assomptions sont particulièrement fondées dans certains types d’yeux, mais peuvent s’avérer source d’erreur dans d’autres.
Ainsi, certaines formules sont plutôt recommandées en fonction de la longueur axiale (yeux courts < 22mm, vs yeux longs > 24 mm) ou de l’existence d’antécédents de chirurgie réfractive cornéenne.
On distinguait initialement et schématiquement deux familles de formules: les formules de régression, et les formules théoriques (ou « exactes »). Dans certaines classifications, les formules de régression sont classées comme des formules de « seconde génération ».
En réalité, il existe toujours une part de « régression » dans les formules théoriques, car il n’est pas possible de prédire avec certitude la position exacte de l’implant dans l’oeil (sa distance avec la cornée) avant la chirurgie. L’apport de l’intelligence artificielle (IA) a permis un gain net en précision et certaines formules de dernière génération incorporent des algorithmes d’IA (ex: PEARL DGS)
Formules de régression
Les formules dites de régression furent parmi les premières à être disponibles. Elles ont été établies de manière rétrospectives à partir de données telles que la mesure de la puissance cornéenne (kératométrie), de la longueur axiale, de la puissance de l’implant posé, et de la réfraction finalement obtenue. Le calcul utilisant la régression vise à établir une équation qui exprime la puissance de l’implant à partir de ces variables dites « explicatives ».
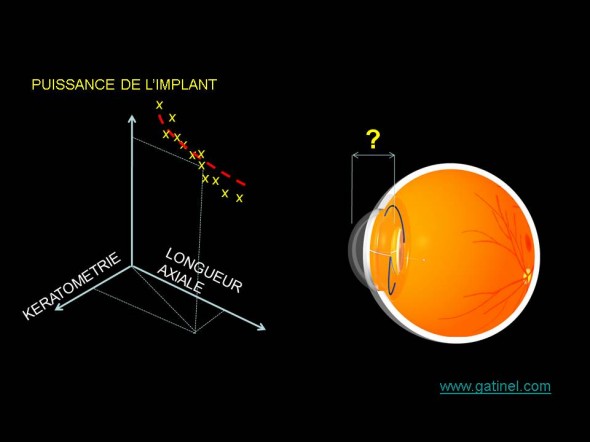
Les formules de régression sont calculées en fonction du lien reliant kératométrie, longueur axiale et puissance de l’implant posé chez des patients emmétropes après l’intervention de cataracte. Elles correspondent à l’équation de la courbe qui épouse au mieux le nuage de point dont les coordonnées correspondent dans cet exemple à la kératométrie, la longueur axiale et la puissance de l’implant posé. La dispersion des valeurs est liée en grande partie aux variations de la position de l’implant dans l’oeil.
Une analogie avec cette méthode serait pour un tailleur d’établir une formule pour prédire au mieux la bonne taille de costume à ses clients à partir de la mesure de leur la taille (en cm) et leur poids (en kg). Muni d’une base de données référençant quelques centaines de clients (et d’un bon logiciel de statistiques), il serait possible à ce commerçant d’établir une telle formule.
La première formule établie à la fin des années 60 par Fyodorov n’était pas une formule de régression, mais une formule théorique de première génération, fondée sur un modèle mathématique de l’oeil où était appliqué un trajet de rayon lumineux. Les déboires rencontrés avec les premiers résultats, qui n’étaient pas que liés à la formule mais aux techniques de mesures, n’ont pas rendu cette approche universelle. La formule de régression SRK fut développée au début des années 80 en tant que formule de régression par Sanders, Retzlaff et Kraft :
P = A − 2.5L − 0.9K
Cette formule peut s’interpréter comme la développement en série de Taylor (premier degré) d’une formule théorique de première génération, où la puissance de l’implant varie linéairement en fonction des variations de L (longueur axiale) et K (kératométrie). Avec ce développement, on obtient une constante (A) dont la valeur peut être modulée pour s’ajuster au mieux au données cliniques. La valeur de la constante A est proche de 118 pour les implants de chambre postérieure. Cette constante est ajustée pour limiter au mieux l’effet des variations de la position effective de l’implant, elles même dépendantes de sa géométrie et son design optique. L est la longueur axiale (en mm) et K la kératométrie moyenne (dioptrie). La constante A est donc censée compenser plus ou moins directement les variations de la profondeur anatomique de la chambre antérieure après pose de l’implant. A une certaine époque pionnière en matière d’implant de cristallin artificiel, ce dernier était fixé contre l’iris. La profondeur anatomique de la chambre antérieure postopératoire était alors très proche de la position de l’implant.
Il est important de saisir qu’une variation de la constante A était directement reportée dans la puissance de l’implant (l’augmenter de 1 revenait à augmenter le résultat du calcul de puissance d’une dioptrie). Quand la formule SRK-T (T pour théorique) fut développée, ses auteurs souhaitèrent conserver ce concept, mais la formule étant théorique, les variations de constante A induisaient un incrément (fixe) de position prédite de l’optique, dont l’effet sur la puissance calculée était indirect. Ce point n’est pas anecdotique, mais il est souvent ignoré, et participe à la mauvaise compréhension du concept de constante et d’optimisation (qui fait l’objet d’une page accessible par le lien situé plus haut).
Cette formule SRK possédait l’avantage d’être simple, à une époque le calcul électronique et informatique était encore peu accessible pour les cliniciens.
Exemple de calcul de puissance d’implant :
A = 116.8, L = 23mm and K = 43D, P = 116.8 − 57.5 − 38.7 = 20.6D. Cette puissance est la puissance calculée pour les milieux intra oculaires (implant situé « dans l’oeil », indice de réfraction proche de 1.33). Dans l’air (indice de réfraction =1), cette puissance serait plus importante.
La formule SRK est aujourd’hui désuète, car elle s’est avérée relativement imprécise pour les yeux « atypiques » (les approximations de type Taylor ne sont précises qu’autour d’une petite zone de valeur, ex: les yeux « moyens »). La relation entre ces paramètres n’est pas linéaire, en particulier l’influence de la longueur axiale. Il est néanmoins intéressant de comprendre les principes à la base du calcul fourni par cette formule (régression), car une approche de ce type est encore utilisée pour estimer la valeur de la position effective de l’implant: étant donné que celle-ci n’est pas mesurable en préopératoire, et que seule une approche prédictive de type « statistique » peut être utilisée.
Les formules théoriques qui sont aujourd’hui utilisées pour le calcul biométrique sont dites « théoriques », car elles sont fondées sur l’application de formules de vergence sur un modèle d’œil théorique. On applique alors virtuellement un trajet de rayons lumineux (près de l’axe optique) au travers des différentes surfaces optiques (dont celle de l’implant). Dans ce calcul, il est nécessaire d’attribuer une position à l’implant: c’est dans la prédiction de cette position que se situe les différences entre les formules théoriques « modernes ».
Les formules théoriques (ou exactes) de calcul d’implant
Les premières formules théoriques permettant de calculer la puissance de l’implant à partir d’un modèle d’oeil simplifié furent baptisées en l’honneur de leur développeur (cette tradition perdure). On distingue rétrospectivement plusieurs génération de formules théoriques, car un simple calcul utilisant la formule de vergence souligne un point important : la position de l’implant dans l’œil ne peut être connue avec certitude avant la chirurgie (l’implant peut se positionner quelques centaines de microns en avant ou en arrière dans le sac capsulaire).
On peut regrouper classer les formules en fonction de leur génération, cette classification étant sujette à certaines variations en fonction des auteurs.
La classification la plus simple distingue les formules théoriques dites de première génération, les formules empiriques – dites seconde génération (voir plus haut), et les formules théoriques modernes – dites de troisième génération.
Formules théoriques de première génération
La formule de Fyodorov fut pionnière, et suivie par les formules de Colebrander (1973), Hoffer (1974) et Binkhorst (1975) (C D Binkhorst fut un ophtalmologiste hollandais qui développa un modèle d’implant clippé à l’iris). D’autres auteurs ont proposé une formule théorique proches: formule de Thijssen, formule de Van der Heijde… Malgré une expression analytique parfois différente au numérateur et dénominateur, ces formules sont quasiment (voire parfaitement) identiques (la formule de Thijseen tient compte de l’épaisseur de l’implant, la formule de Colebrander de la position des plans principaux de la cornée, etc.)
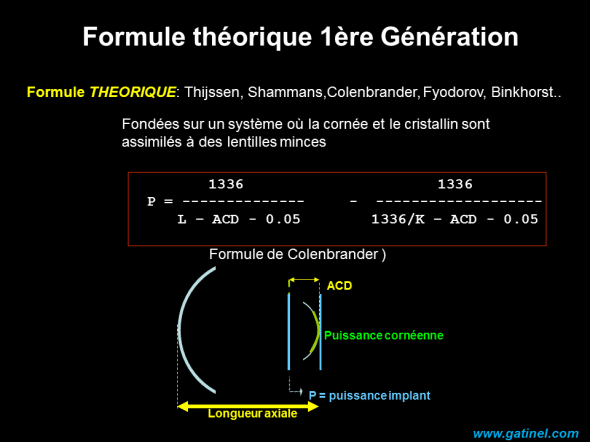
Les formules théoriques reposent sur l’utilisation d’un modèle d’oeil simplifié et de formules de vergences. La valeur utilisée pour la position effective de l’implant (C) est forcément arbitraire. On conçoit aisément que les formules ultérieures aient eu comme moteur principal d’accroître la justesse de la prédiction de la position effective de l’implant. La formule de Colebrander est légèrement modifiée vis à vis de la formule théorique obtenue par calcul de vergence: la position effective de l’implant est accrue de 0.05 mm, cette distance correspondant à la position du plan principal objet de la cornée – voir pouvoir optique paraxial de la cornée).
Les formules théoriques reposent sur l’utilisation d’un modèle d’oeil simplifié et de formules de vergences. La valeur utilisée pour la position effective de l’implant (ACD pour « Anterior Chamber Depth ») est forcément arbitraire. La formule de Binkhorst II utilisait une valeur d’ACD prédite proportionnelle à la longueur axiale :
ACD postop = ACD preop x (L/23.45)
On conçoit aisément que les formules ultérieures aient eu comme moteur principal d’accroître la justesse de la prédiction de la position effective de l’implant. La formule de Colebrander est légèrement modifiée vis à vis de la formule théorique obtenue par calcul de vergence: la position effective de l’implant est accrue de 0.05 mm, cette distance correspondant à la position du plan principal objet de la cornée – voir pouvoir optique paraxial de la cornée).
Les formules théoriques modernes découlent de ces formules initiales: ces formules exactes diffèrent dans la manière dont elles prédisent la position effective de l’implant en post opératoire (c’est à dire la position de l’implant dans l’œil après l’intervention). Les formules de première génération connurent un succès mitigé car les techniques de mesure de la longueur axiale n’étaient pas aussi précises qu’aujourd’hui : on utilisait à l’époque une méthode contact où une sonde émettait des ultrasons au contact de la cornée: la vitesse de propagation des ultrasons pouvait fluctuer selon le degré de cataracte, et l’examinateur, en exerçant une pression involontaire sur la cornée lors de la mesure pouvait réduire artificiellement la valeur de la longueur axiale.
L’introduction de la mesure interférométrique en 1999 (IOL Master, Zeiss), ainsi que les formules théoriques de seconde génération (c’est à dire les formules de calcul de troisième génération!), où la valeur de la position effective de l’implant est fonction de divers paramètres (et permet une meilleure prédiction de la puissance de l’implant) ont généralisé l’utilisation des formules théoriques.
Hoffer fut en 1982 un des premiers à tenter de corréler la position effective de l’implant à la longueur axiale: les yeux plus longs possèdent généralement une chambre antérieure plus profonde que les yeux plus courts. Cette relation entre longueur axiale et profondeur de la chambre antérieure définit les formules de seconde génération.
La relation utilisée par Hoffer pour relier la position de l’implant avec la longueur axiale était :
ELP = 2.93 x AL – 2.92
Formules théoriques dites de troisième génération
Elles se caractérisent par l’utilisation de la kératométrie pour parfaire la prédiction de la position effective de l’implant.
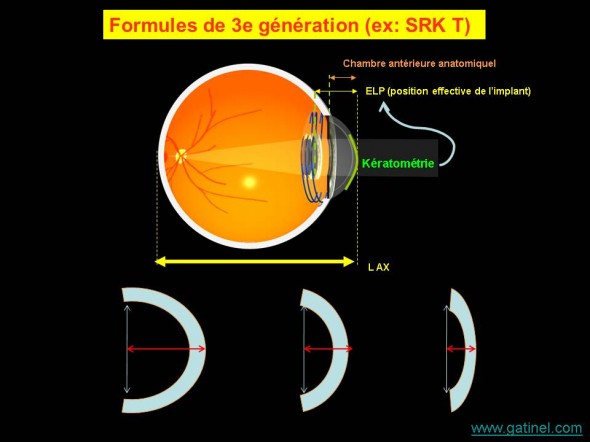
Les formules de 3e génération sont basées sur l’utilisation d’algorithmes particuliers destinés à améliorer la prédiction de la position effective de l’implant à partir de la valeur de la kératométrie; une cornée plus cambrée suggère une flèche (donc une profondeur de chambre) accrue.
Formule de Holladay
Holladay a proposé d’utiliser la courbure cornéenne comme prédicateur de la position finale de l’implant, en insistant sur la différence entre la valeur de profondeur de chambre antérieure ‘sommet cornéen à iris « aACD » pour Anterior Chamber Depth) et la distance entre sommet cornéen et implant. La différence (distance iris-implant) fut baptisée « Surgeon Factor » (SF). Le calcul de la valeur de SF pouvait alors faire l’objet d’une régression faisant intervenir la constante A de l’implant. La profondeur de chambre antérieure est prédite à partir d’une régression portant sur la longueur axiale ET la kératométrie.
Formule SRK T
C’est en s’inspirant de cette approche que Retzlaff (le « R » du trio d’auteurs à l’origine de l’acronyme SRK) proposa la formule SRK T (T pour Théorique), mais en conservant le concept de constante A (probablement pour ne pas contrarier les utilisateurs encore nombreux de la formule de régression SRK). Cette constante A était convertie en position effective de l’implant à partir d’une formule linéaire.
ELP = Flèche cornéenne + 0.62467 x A – 68.747 – 3.336
La flèche cornéenne est un paramètre qui permet de relier la courbure cornéenne à la distance cornée/iris. De cette estimation naît un problème chez les patients opérés de chirurgie réfractive: la courbure cornéenne est modifiée chirurgicalement, et n’est plus un bon prédicateur de la profondeur de la chambre antérieure.
En raison du mécanisme de régression utilisé pour conserver les valeurs établies de constante A déjà établies pour les implants de l’époque, il semble à première vue qu’un ajustement de la constante A d’une certaine valeur (ex une unité) produise une augmentation de 1D (ou proche) de la puissance de l’implant (pour atteindre la même cible réfractive). Ceci vaut surtout pour les yeux moyens.
Formule de Hoffer Q
De même, Hoffer proposa en 1992 la formule de Hoffer Q, utilisant une formule quadratique pour prédire une profondeur de chambre antérieure théorique personnalisée à partir de la kératométrie; une fois celle-ci obtenue, elle était alors utilisée comme base pour un réajustement fonction de la kératométrie et de la longueur axiale.
Les formules de 3e génération sont employées en routine pour la chirurgie de la cataracte. Elles excellent plus particulièrement dans certaines conformations oculaires (yeux courts, yeux longs, etc.). La figure suivante résume les indications préférentielles de ces formules, en fonction de la longueur axiale du globe oculaire concerné.

La longueur axiale détermine généralement le choix de la formule de 3e génération utilisée pour le calcul biométrique
Les formules les plus récentes de 3e génération accordent moins (voire pas) d’importance à la kératométrie pour le calcul de la position prédite de l’implant (ELP). Ceci les rend particulièrement intéressante dans les situations où la kératométrie a été modifiée chirurgicalement, soit pour les yeux ayant bénéficié dans le passé de chirurgie réfractive (LASIK, PKR, kératotomie radiaire, etc.)
Formule de Olsen
Elle est fondée sur l’utilisation de divers paramètres du segment antérieur, comme la profondeur de la chambre antérieure (anatomique) préopératoire pour établir un algorithme utilisant cette valeur pour améliorer la prédictibilité du calcul de la position effective de l’implant. Dans cette formule, l’influence de la kératométrie sur la position effective de l’implant est nulle.
Formule de Haigis
En 1999, Haigis a proposé d’utiliser 3 constantes pour prédire la position effective de l’implant, fondées sur les caractérsitiques anatomiques de l’oeil et de l’implant utilisé. Comme la formule de Olsen, la kératométrie n’est pas utilisée pour prédire la position effective de l’implant. En revanche, le type d’implant, la profondeur de la chambre antérieure (préopératoire) et la longueur axiale sont inclus dans le calcul de la position effective de l’implant (ELP).
Certaines formules ne sont pas publiées in extenso (Holladay II) ou font l’objet de travaux plus théoriques que d’applications pratiques (ray tracing). Certains auteurs considèrent ces formules comme de 4e voire 5e génération.
Formule de Holladay II
Hollday a développé une formule où divers paramètres anatomiques du segment antérieur de l’oeil comme le diamètre blanc à blanc (diamètre de la cornée), ainsi que l’age du patient, le sexe, la réfraction préopératoire sont utilisés pour prédire une valeur appelée ESF pour Etimated Scaling Factor. Cette valeur est alors multipliée par la celle de la position effective de l’implant prédite par le fabricant. Cette formule, proposée en 1996, n’a jamais été publiée. Elle est disponible sur internet moyennant un abonnement payant.
Formule de Barrett (Barrett Universal II formula)
La formule de Barrett repose sur l’utilisation de la kératométrie, de la longueur axiale, de la profondeur de la chambre antérieure. Le diamètre blanc à blanc (diamètre du limbe sclérocornéen) et l’épaisseur du cristallin sont des données optionnelles. Barrett a également développé une formule de calcul pour la puissance du cylindre (astigmatisme) des implants toriques, et une formule destinée à estimer de manière plus précise la puissance cornéenne globale (Barrett true K).
Intelligence artificielle/ Apprentissage profond (deep learning).
La chirurgie de la cataracte est la procédure la plus effectuée en nombre, toutes interventions chirurgicales confondues. Il existe des centaines de milliers voire des millions de données potentiellement exploitables, pour améliorer les formules existantes, c’est à dire pallier l’incertitude relative à la position de l’implant (effective lens position) dans l’oeil à la fin de l’intervention. L’utilisation d’algorithmes « intelligents », ou plutôt rendus performants par la masse des données qui les nourrissent est une piste actuellement prometteuse en biométrie oculaire.
La formule de calcul Hill-RBF représente une première approche dans le domaine. Elle est toutefois conçue à partir des données d’un biomètre particulier (Haag-Streit Lenstar) et de deux types de lentilles intraoculaires monofocales. Il est toutefois possible d’extrapoler les résultats du calcul à d’autres types de lentilles, et d’utiliser les données de biomètres concurrents pour effectuer les calculs.
Nous avons également travaillé à la mise au point d’une formule reposant sur l’intégration de données par un algorithme d’intelligence artificielle afin d’améliorer encore la précision du calcul biométrique des yeux opérés de chirurgie de la cataracte, et avons présenté les résultats préliminaires de ce travail (récompensé par un award) lors du congrès de l’ASCRS en Mai 2019 (San Diego, USA). Nous avons réalisé une nouvelle formule biométrique: PEARL DGS). Cette formule est conçue pour améliorer la précision du calcul biométrique, en particulier pour les yeux précédemment opérés de chirurgie réfractive.
Ray tracing
L’utilisation d’un logiciel capable d’effectuer la simulation du tracé de rayons à travers un oeil modèle, dont les surfaces cornéennes peuvent être données par des mesures topographiques effectuées avant l’opération (face antérieure, face postérieure, épaisseur de la cornée). Le ray tracing permet de faire un calcul de lancé de rayons en dehors des conditions paraxiales (optique de Gauss). De ce fait, le ray tracing prend en compte l’asphéricité des surfaces cornéennes. En revanche, comme pour les autres formules optiques, la position effective de l’implant ne peut être connue à l’avance. Ce type de calcul n’est pas fréquemment utilisé, car il nécessite l’utilisation d’un logiciel spécifique (Oculix) et la supériorité de cette approche sur les formules de troisième génération n’est pas démontrée.

Si vous n’aviez rien contre le port de lunettes de près, il est effectivement possible de choisir une puissance d’implant destinée à « emmétropiser » votre deuxième oeil. Il faut expliquer votre choix au chirurgien qui devrait entériner votre souhait.
Je dois subir prochainement une chirurgie de la cataracte pour mon deuxième oeil . Mon premier à ete opérer ( avec succès …je l’espère il y a seulement 2 semaines …bref ne nous excitons pas ) Cela semble bien aller . Il a été corriger pour une myopie d’environs moin 9 . Ce premier oeil à perdu à cause du glaucome tout le cadran supérieur ( de 9 @15 hre ) de son champs visuel . 6 mois auparavant j’ai recu un stent Xen pour stabiliser la PIO de ce dernier . La proposition de puissance pour l’oeil restant à opérer est moindre et la chirurgienne parle donc de ‘monovision’ . Il sera ainsi plus facile de gérer ma proprioception des objets proche et cela facilitera aussi la lecture . Mais j’ai des doutes et j’ai dit à la chirurgienne que j’aimerais pleine puissance de correction comme le premier oeil déjà opérer. Cela ne permettrais pas grand chose pour le travail de près ( lecture bricolage etc ) mais puisque j’ai porter de fort verres pour la myopie depuis 50 ans ( j’en ai 62 ) alors n’avoir qu’a porté des lunettes pour voir de proche ne m’inquiete pas trop . Mon objection de la proposition vient du fait que si le glaucome progresse dans l’oeil ayant le stent je n’aurai que celui qui ne sera pas pleinement corriger sur lequel me fier . Que dois-je choisir ? Je suis à 2 semaine de la 2ième op et il faut commander la lentile intraoculaire approprier très bientot . Difficile d’obtenir des avis . Merci
Vraiment, vous êtes, un grand, docteur.
On vous aime, respect beaucoup.
Je vous souhaite une bonne santé.
Bonjour,
J’ ai un oeil amblyope et depuis que j’ai été opéré de la cataracte des deux yeux je voie trouble, j’ai mal a la tête, j’en ai marre que puis je faire ??
Je vais voir le chirurgien qui m’a opéré demain mais je m’aperçois que je ne suis pas le seul et cela m’inquiète.
En cas de résultat réfractif décevant après chirurgie de la cataracte, une solution simple et efficace consiste à effectuer une correction de chirurgie réfractive (LASIK ou PKR) au plan cornéen. C’est certainement préférable que d’envisager un changement de votre implant, ou l’insertion d’un implant secondaire (piggy back). Il faut effectuer un bilan classique de chirurgie réfractive pour vérifier votre opérabilité.
Bonjour
Je viens d’être opéré de la cataracte
Je suis fort myope – 13
Le résultat n’est pas bon je reste avec une myopie encore importante
Il y a eu une erreur de calcul de la puissance de l’implant
L’implant qui a été posé est le suivant modèle +20.0 d
19dxxb35
Diametre b 6 mm
Diamètre t 11.40mm
Pourriez me dire si il y a des solutions pour améliorer ma vision
D’avance merci
Cordialement
Les commentaires sont faits pour les questions ! A priori, un implant de faible puissance laisse présager d’une plus grande myopie avant l’intervention. Cela dit, certaines caractéristiques propres aux évolution des implants peuvent moduler cette appréciation (rôle de la constante A, qui est un paramètre d’origine statistique destiné à « centrer » améliorer la précision du calcul de la puissance des implants). Il faudrait retrouver la valeur de cette constante pour l’implant de 1994 afin de mieux comparer les puissances dioptriques « réelles » des implants posés.
Bonjour,
Excusez moi il ne s’agit pas d’un commentaire (mais je vous remercie pour la qualité de votre article qui me parait très complet) mais d’une question : chez un patient âgé de 69 ans, fort myope, ayant un glaucome très asymétrique , est il possible a posteriori d’estimer le degré d’asymétrie de sa myopie à partir des données de puissance de ses 2 ICP l’un posé en 1994 (puissance 17) l’autre posé en 2018 (puissance 8) ? Car j’ai l’impression que l’oeil le plus myope n’est pas celui que j’attendais !
Merci.
Martine Perrier. Médecin retraitée.
La formlule SRK-T est adapté aux yeux dont la longueur awiale est standard (>22 mm), et dont les caractéristiques biométriques ne laissent pas augurer d’une « surprise » liée à la mauvaise prédiction de la position de l’implant après l’intervention (ex: cornée plates, chambres antérieures atypiques, etc etc.). En cas de modification préalable de la kératométrie (ex: chirurgie réfractive), il est préférable d’utiliser une formule de type Haigis, où la kératométrie n’est pas utilisée pour prédire la position de l’implant (la formule n’utilise que les données relatives à la longueur axiale et la profondeur anatomique de la chambre antérieure). Pour les yeux courts, la formule de Haigis « fonctionne » bien, aussi bien que la formule Hoffer Q dans mon expérience.
Bonjour,
pour les patients opérés de chirurgie réfractive au laser, la formule haigis serait donc la plus adaptée car elle ne tient pas du tout compte de la kératométrie ?
Pour un oeil avec une longueur axiale standart j’utilise la formule SRK-T, or vous dites qu’elle est plutôt utilisée pour un oeil très long, qu’elle formule doit-on utiliser alors ?
Merci d’avance pour votre réponse
JE VOUS REMERCIE ENORMENT POUR CES INFORMAIONS SUR LES DIFFERENTES DE CALCUL DES IMPLANTS INTR OCCULAIRE.
CELA M’AIDE BEAUCOUP EN TANT QU’INGENIEUR SPECIALISTES DES QUIPENMENTS OPHTALMOLOGIQUES EN COTE D’IVOIRE ET DANS LA SOUS REGIONS