Paraxial optics for IOL power calculation

This section of the website is dedicated to calculating the power of an artificial intraocular lens (IOL) implant in cataract surgery, which is the most frequently performed surgical procedure in the world, all specialties combined.

While performing a biometric examination and using calculation formulas is a trivial act for the ophthalmologist, the underlying mechanisms that lead to the determination of a power intended to achieve a desired refractive goal are less familiar. Furthermore, it may be desirable and certainly interesting to locate the elements necessary for a good understanding of the calculation of implant power in a perspective linking the elementary properties of light to more advanced characteristics.

Thus, the first part (From light speed to Snell’s law) is devoted to a reminder of the properties which govern the movement of light within the propagation media. It introduces the notion of refractive index, and the principle of least action, which states that between two points, light takes the shortest path duration. From this property follows the law of Snell Descartes. The notion of vergence is discussed at the end of this page.

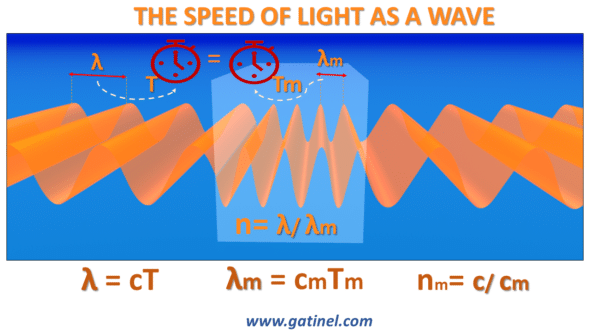
Light slows down in dens material such as the cornea, or aqueous humor, but its frequency remains constant.

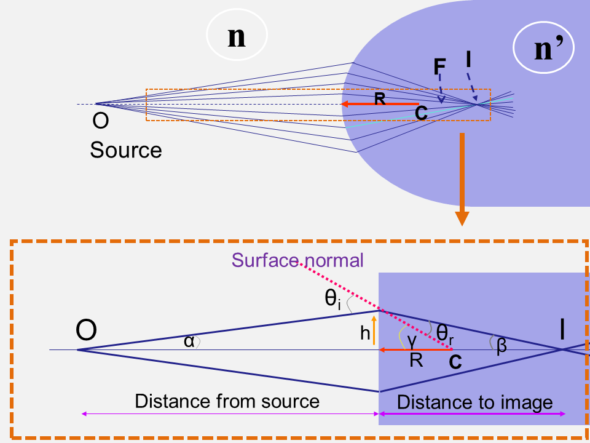
The study of vergence is deepened in the second part (From Snell’s law to vergence formula), which develops the steps necessary to establish the vergence formula in paraxial conditions.

Paraxial approximation conditions in a diopter

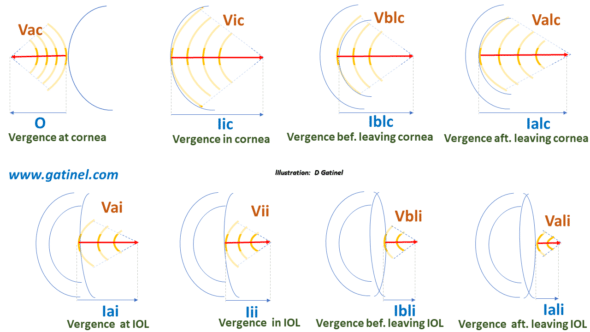
Establishing the equality leading to the thin lens IOL power calculation formula.In the third part, the vergence formula is used and propagated in a thin lens pseudophakic eye model of vergence  (Computing vergence in the pseudophakic eye).

Computational steps for vergence propagation through the pseudophakic eye.

From the mastery of these concepts, we can establish a paraxial formula for calculating the power of the implant in an eye model equipped with « thin lenses » (Thin lens IOL power computation).

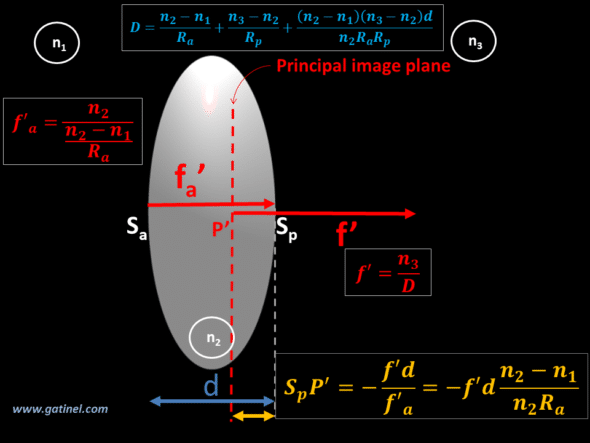
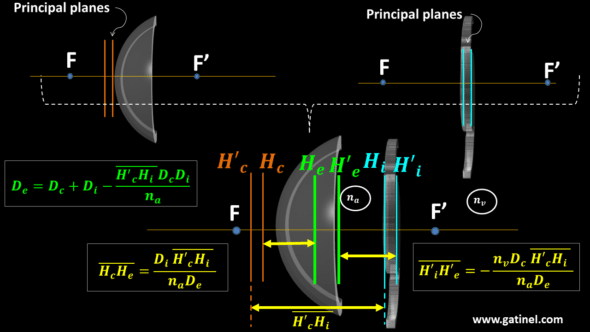
Switching to a more complex model, with thick lenses, requires the introduction of certain concepts such as that of the principal planes. For didactic reasons, the explanations will be particularly detailed in order to familiarize the reader with these concepts often little developed elsewhere. The formulas which allow locating the position of these theoretical planes in the case of a simple thick lens are reported (Principal planes: explanations).

Determination of the position of the principal image plane

The following parts are successively devoted to paraxial analytical expressions related to the cornea (Paraxial power of the cornea) and to the IOL (Paraxial power of the IOL). The use of a thick lens model allows consideration of certain elements relating to the design of the implant, such as its thickness and the ratio between the curvatures of its front and rear surfaces (Coddington shape factor). The couple cornea + IOL can be reduced to a single set characterized by its focal lengths and the position of its principal planes (Paraxial power of the pseudophakic eye).

Thick lens paraxial pseudophakic eye model.

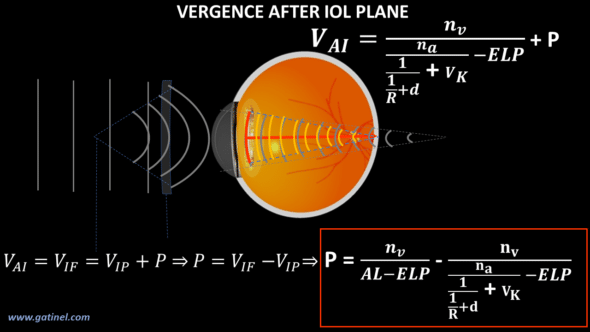
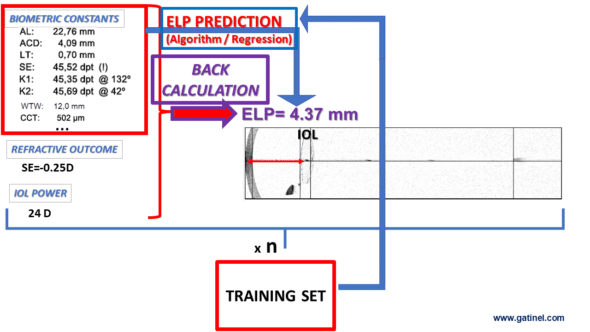
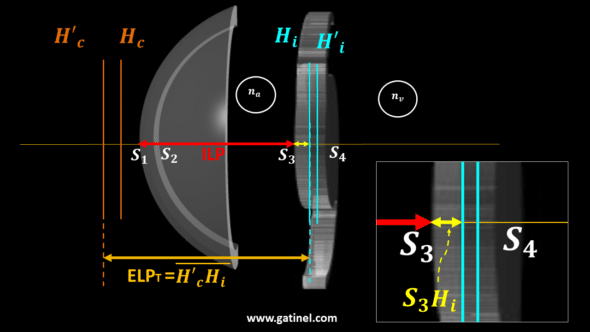
Once these elements have been established, a paraxial pseudophakic eye model can be constructed (Thick lens paraxial eye model) so as to be able to establish the calculation formulas useful in this context, such as the determination of the theoretical thick lens position from the preoperative biometric elements, of the power and the design of the IOL placed, as well as the postoperative refraction (Back calculation of the Effective Lens Position). This provides building blocks for the training set and training algorithm to predict the position of an implant in the anterior segment of the eye.

Another interesting aspect in this context is to be able to predict the refraction of a pseudophakic eye based on variations related to the type of implant placed (Refraction of the pseudophakic eye).

Last but not least, the conjunction of all these data makes it possible to establish the methods of a formula for calculating the power of the implant from data collected preoperatively and the characteristics specific to the design of the implant considered as a thick lens (Thick lens IOL power calculation).