Amplification de la lumière laser
Nous avons vu comment l’émission stimulée pouvait produire de la lumière LASER, aux propriétés particulières: cohérence, pureté spectrale, aspect directionnel. Il faut cependant avoir à l’esprit que déclencher une émission stimulée ne représente qu’une partie du travail consistant à réaliser une source utilisable de lumière laser: sans amplification secondaire, il n’est pas possible de générer un faisceau de lumière LASER à la sortie de la cavité.
Limites de l’émission stimulée seule
Le scénario suivant permet de comprendre pourquoi l’amplification de la lumière laser pour générer un faisceau à la sortie de la cavité.
Nous pouvons imaginer qu’une fois l’inversion de population créée dans un milieu, un premier atome se désexcite spontanément, engendrant un premier photon. Ce photon a de grande chance de rencontrer à son tour un second atome excité, et provoquer la création d’un second photon. Un de ces photons peut continuer son trajet et sortir de la cavité – ou être absorbé par un des atomes non excités (même si leur proportion est moindre que celle des atomes excités), …et l’autre provoquer une nouvelle désexcitation, conduisant à l’apparition d’un nouveau photon, avant que ces deux-là de sortent également du milieu. On aura alors engendré 3 photons… là où il en faudrait de l’ordre de 10 19 pour produire une énergie lumineuse d’un Joule !
Pour amplifier et perpétuer le phénomène d’émission stimulée, il faut réussir à maintenir les photons engendrés par l’émission stimulée dans la cavité contenant le milieu excité; pour que ce phénomène d’émission stimulée atteigne une certaine ampleur. Pour atteindre cet objectif, on utilise des miroirs que l’on place de part et d’autre du milieu, sur lequel les photons vont rebondir, et seront renvoyés vers le milieu.
Ces miroirs ne sont pas véritablement les mêmes que ceux des salles de bain ; leur surface n’est pas recouverte d’un film métallique mais de couches multiples, d’indice réfractif différent, de manière à créer les conditions requises pour que les longueurs d’ondes lumineuses propres au rayonnement laser généré s’y reflètent. Nous verrons plus loin l’importance de que revêtent la courbure et la distance séparant ces miroirs, entre lesquels les propriétés ondulatoires de la lumières induisent des phénomènes de « résonance ». La cavité laser munie de ces deux miroirs se comporte alors comme un « résonateur ». Un de ces miroirs est partiellement transparent, de manière à produire en sortie le rayonnement laser : ce rayonnement peut alors être utilisé pour les fins requises: le rayonnement émis à la sortie de la cavité a été amplifié entre les miroirs; dont la courbure et l’alignement sont conçus pour favoriser l’émission d’une lumière directionnelle.
Pertes et gain de la cavité laser
Le rayonnement produit par la cavité vers l’extérieur est toutefois « perdu » pour l’entretien de l’émission stimulée : si la transparence du miroir est de 5%, cela veut dire que sur 100 photons incidents, 5 sortiront pour générer le rayonnement laser, les 95 autres seront réfléchis et renvoyés vers le milieu pour produire de nouvelles désexcitations et générer d’autres photons. Il faut donc que le gain après ce trajet aller-retour soit au moins supérieur aux 5% représentés par la perte du miroir de sortie, sous peine de voir le processus d’émission stimulée s’éteindre, « faute de combattants » (ou plutôt faute d’un nombre suffisant de photons).
De plus, d’autres facteurs que la sortie d’un certain nombre de photons ont pour conséquence de réduire l’ampleur de l’émission stimulée (c’est-à-dire la probabilité qu’un photon émis par stimulation rencontre un atome excité, et produise un second photon par désexcitation). En effet, quand les photons émis par émission stimulée rencontrent des atomes excités, ils produisent à leur tour une nouvelle émission stimulée, mais … au prix d’une diminution du nombre d’atomes excités présents dans le milieu. Il faut donc constamment compenser cette réduction par un apport extérieur d’énergie (excitation du milieu). Par ailleurs, les photons produits par émission stimulée ont également vocation à sortir de la cavité du laser à un moment donné, et certains sont également absorbés, diffractés, et donc perdus pour entretenir le phénomène d’émission stimulée.
Au total, cet antagonisme subtil pertes et gain a deux conséquences :
– Il faut atteindre un certain seuil d’émission stimulée pour obtenir un gain, c’est-à-dire que l’énergie fournie au milieu permettent une inversion de population et le début d’une l’émission stimulée entretenue, c’est-à-dire supérieure aux pertes de la cavité. Dans ce cas, le nombre de photons produits par émission stimulée croît progressivement, mais pas indéfiniment : il intervient nécessairement une « régulation » qui fait que le gain obtenu une fois l’émission stimulée et la résonance dans la cavité demeure constant (ce gain est la différence entre l’apport de l’émission stimulée et les pertes par absorption spontanée, diffraction, etc. dans la cavité). Ceci survient quelle que soit la puissance fournie au système. Pour comprendre cet équilibre, il faut se souvenir que plus il y a de désexcitations et d’émission stimulée, plus on produit de photons identiques, mais moins il y a d’atomes susceptibles de rencontrer ces photons…
– Si l’on accroit l’énergie fournie au système, on n’augmente pas le gain, mais uniquement l’intensité (la puissance) de sortie du laser. On pourrait objecter qu’il suffit d’augmenter la transmission du miroir de sortie pour augmenter la puissance obtenue en sortie : ceci risque en réalité de réduire le nombre de photons présents dans la cavité et donc réduire le taux d’émission stimulée… Il existe pour chaque laser une transmission optimale, qui permet de produire le maximum de puissance possible sans réduire la puissance interne du laser.
Pour une puissance constante fournie au laser, le gain et donc la puissance circulant dans le laser varient (oscillent) au fil du temps, car l’augmentation de la production de photons par émission stimulée induit mécaniquement une réduction de la proportion des atomes excités, et vice versa.
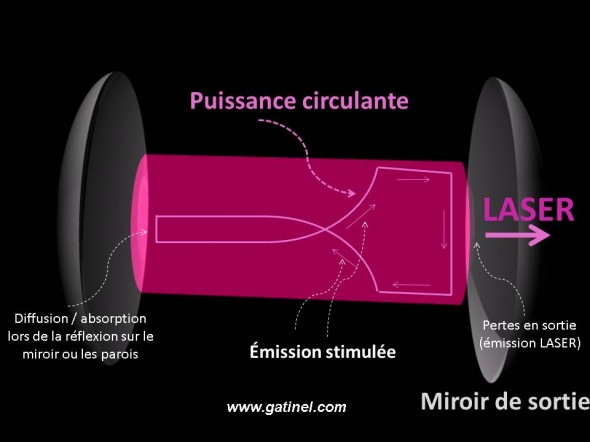
Représentation schématique de la puissance circulante au sein d’une cavité laser: le gain lié à l’émission stimulée, qui se produit quand le flux de photons rencontre le milieu excité permet de compenser les pertes liées à l’émission lumineuse en sortie, et les phénomènes d’absorption et de diffusion.
Nous avons donc compris pourquoi la cavité contenant le milieu excité devait être encadrée de miroirs, car ceci permet aux photons engendrés par l’émission stimulée de perpétuer celle-ci. Toutefois, outre sa composante corpusculaire (les photons), la lumière est dotée de propriétés ondulatoires (l’énergie des photons est proportionnelle à leur « fréquence »). Parce qu’elle possède une certaine longueur dans l’axe des miroirs; a cavité va faire office de résonateur pour certaines fréquences lumineuses, ce qui a d’importantes conséquences sur la qualité du rayonnement produit.
L’illustration suivante est une photo de la cavité d’un laser excimer utilisé pour la chirurgie réfractive (laser EX500, wavelight).

Cavité laser (excimer) et orifice de sortie (laser EX500 Wavelight)
Caractéristiques du résonateur, conséquences sur le rayonnement LASER
Avant d’aborder les caractéristiques en fréquence du rayonnement produit par la cavité, revenons sur le fait qu’à l l’intérieur du résonateur, les photons émis par émission stimulée circulent d’un miroir à l’autre : le profil d’énergie créé dans un plan transversal épouse un profil en « cloche », dont le pic est situé au centre de la cavité. Ce profil à une allure « Gaussienne », on parle de profil Gaussien. Il présente une largeur notée « w » (pour ‘waist » en anglais) qui correspond en terme énergétique à la largeur définie pour le faisceau laser. La définition de la largeur du profil d’énergie LASER est arbitraire, car le faisceau n’a pas de bords nets : par convention, quand à une distance radiaire w du pic central, l’intensité n’est plus que de 13% environ, on considère que l’énergie LASER est négligeable.
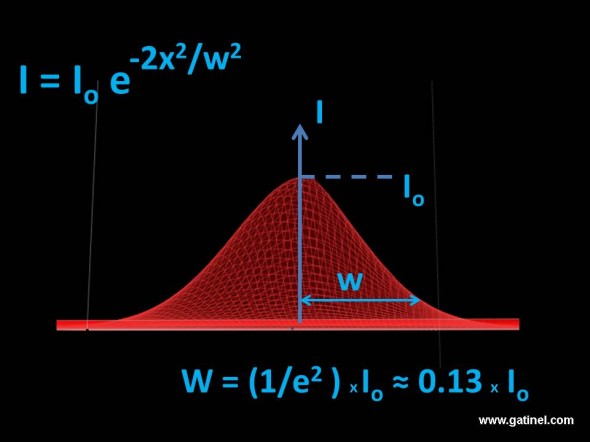
La largeur (rayon) du faisceau gaussien au sein d’une cavité laser (mode principal) est une fonction du pic gaussien d’intensité mesuré dans le plan transversal (parallèle à l’axe des miroirs et perpendiculaire à l’axe de la cavité). Cette largeur est définie comme la distance radiale à laquelle l’intensité du faisceau n’est plus que de 13% de celle du pic central. Dans cette représentation, le profil est étudié en coupe transversale (les miroirs de la cavité seraient orientés verticalement, dans l’axe correspondant à l’intensité)
La formule qui fournit le profil d’intensité du faisceau gaussien est I = Io exp ( -2x2/w2).
Il ne faut pas confondre l’intensité du faisceau gaussien et sa courbure : l’intensité est égale au carré de l’amplitude du front d’onde de lumière cohérente qui se propage dans la cavité et « résonne » entre les miroirs.
Le rayon de courbure du faisceau gaussien concerne sa direction de propagation, et est celui du front d’onde que forment les trains de lumière cohérente (il ne faut pas confondre le rayon de courbure, et le rayon qui correspond à la dimension du faisceau). Le rayon de courbure est « infini » au niveau du diamètre minimum du faisceau (ce diamètre à pour rayon wo), puis décroit rapidement avant de croitre à nouveau.
Une formule permet de calculer la largeur du faisceau à une distance de propagation donnée, si l’on connait son rayon minimal (wo). Ceci revêt une importance, car on peut jouer sur le paramètre wo pour ajuster le rayon du faisceau de manière à ce qu’il est la dimension souhaitée lorsqu’il atteint sa cible.
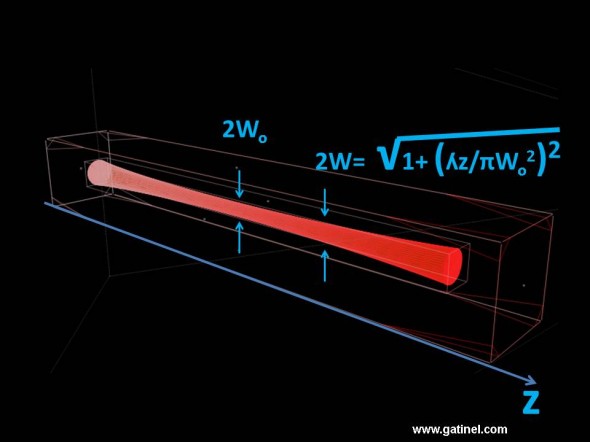
2W représente la largeur (le diamètre) du faisceau laser après une propagation sur une distance de Z mètres depuis son diamètre minimal (w0). Pour une distance entre instrument et œil, de quelque cm, on peut calculer qu’un faisceau de lumière infra rouge (émis par un laser Nd:YAG) de longueur d’onde égale à 1.06 microns subit un élargissement négligeable (de l’ordre du micron). Si ce faisceau se progageait jusqu’à la lune, son diamètre atteindrait toutefois quelques centaines de kilomètres. Il est important de noter que plus Wo est grand, et moins le faisceau diverge, et inversement.
Il est également possible de calculer le rayon de courbure du faisceau gaussien se propageant dans la cavité laser : ceci peut s’avérer utile pour concevoir la géométrie optimale des miroirs qui encadrent le résonateur. On construit une cavité dont on connait bien sûr la longueur: on peut alors calculer la courbure du front d’onde de l’oscillation laser à une distance donnée de l’endroit où le faisceau gaussien a un rayon minimum (wo). Il suffit ensuite de fabriquer des miroirs qui ont le même rayon. En effet la direction de l’énergie qui circule dans la cavité est perpendiculaire à l’enveloppe du front d’onde, et en chaque point du miroir ainsi conçu, les rayons réfléchis ont le même angle que les rayons incidents. Dans cette configuration, la cavité de résonance du laser sera dite « stable ». Il existe une relation mathématique qui relie les rayons de courbure des miroirs, la distance qui les séparent, avec la possibilité d’induire une stabilité au niveau de la cavité du laser.
Il est intéressant de noter que cette condition est indépendante de la longueur d’onde, et donc du type de radiation émise par le milieu excité. Cependant, la nature ondulatoire de la lumière fait que seuls certains rayonnements, de longueur d’onde spécifique, peuvent être mis en « résonance » dans une même cavité.
Modes LASER longitudinaux
Pour une longueur de cavité donnée (L), les rayonnements qui sont susceptibles de résonner de manière longitudinale (d’un bout à l’autre de la cavité) sont ceux pour lesquels un nombre entier de demi-longueur d’ondes peut s’inscrire entre les miroirs.
Cette condition s’exprime comme : n x (ʎ/2)= L où n est un nombre entier.
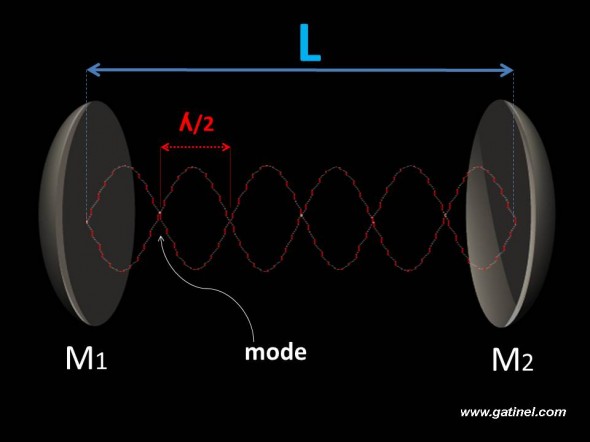
Un rayonnement peut être amplifié entre les miroirs (M1 et M2) si la position de ceux-ci correspond à un « mode »; la condition est remplie quand la distance entre les miroirs (L) est égale à un nombre entier de demi longueurs d’onde. A l’endroit des modes, l’amplitude du champ électromagnétique est nulle.
Les longueurs d’onde pouvant donc résonner sont données par :
ʎ = 2 L/n
On peut convertir cette expression dans le domaine fréquentiel :
Fréquence et longueur d’onde dans le vide sont reliées par : ʎ =c/F (c : vitesse de la lumière)
On obtient la formule qui fournit les fréquences pouvant résonner dans une cavité de longueur L :
Fn = n (c/2xL), où n est un entier
Les fréquences résonnantes sont séparées d’intervalles de (c/2xL).
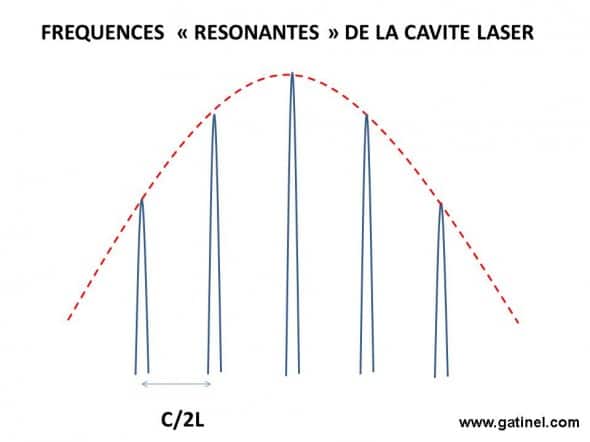
L’intervalle entre les fréquences résonnantes situées de part et d’autre de la fréquence principale au sein d’une cavité laser ne dépend que de la largeur de celle-ci, et non du milieu utilisé pour générer le rayonnement laser. Plus la cavité est courte, et plus l’écart entre les fréquences est important, et inversement. Pour restreindre la gamme de fréquence émises, il est donc nécessaire d’utiliser une cavité plus longue. Pour une cavité de 30 cm, C/2L = 5 x 10 8 Hz, soit 500 Mz. A ce stade, une question peut être : est-ce que l’émission stimulée dans une cavité procure une gamme de rayonnement plus large autour du pic principal que 500 MH2? La réponse est oui !
De ce fait, une cavité laser possède la géométrie requise pour produire un spectre de fréquence correspondant à différents modes longitudinaux. Ceci survient en pratique car contrairement au modèle simplifié de l’émission stimulée (restreinte à une transition énergétique équivalente à une fréquence démission unique), les phénomènes d’émission stimulée provoquent l’émission d’un rayonnement dont le spectre en fréquence n’est pas restreint à une fréquence, mais concerne une large bande passante. En voici quelques unes des raisons:
– Les électrons n’occupent pas des niveaux énergétiques aussi discrets que le modèle simplifié suggère
– Des phénomènes complexes comme l’effet Doppler optique induisent des variations de fréquence des photons émis pour les lasers dont le milieu est gazeux : les atomes ou molécules constitutives de ces gaz sont en mouvement rapide, ce qui induit un élargissement des fréquences d’émission photonique.
– La pression intra cavitaire pour les lasers à gaz influe sur la probabilité de rencontre d’un atome ou molécule excité : plus cette probabilité est faible (moindre pression, moindre nombre de molécules) et plus la bande passante de la cavité laser est étroite, et inversement.
Par exemple, le laser à gaz (Hélium Néon) émet un rayonnement laser composé de plusieurs fréquences, en raison des différentes transitions de l’atome de Néon, qui est excité par collision avec les atomes d’Hélium. La plus intense correspond à une longueur d’onde visible dans le rouge (632.8nm) : l’élargissement en fréquence lié à l’effet Doppler est proche de 1.4 GHz : cet élargissement autorise toutefois une longueur de cohérence proche de 20 à 30 cm. Si on arrive à réduire cette bande passante à 1 Mhz (en « purifiant » le rayonnement émis), la longueur de cohérence peut atteindre plusieurs centaine de mètres.
En fonction de l’application envisagée, diverses méthodes existent pour « purifier spectralement» le rayonnement émis par le laser. On peut par exemple positionner un élément dispersif au centre de la cavité (prisme, et/ou réseau diffractif), de manière à faire dévier certains rayonnements de longueur d’onde (donc des fréquence particulière) de l’axe de la cavité.
A l’inverse, il existe un type de laser émettant des pulses ultra brefs, où l’utilisation d’une plage de rayonnement de différentes fréquences consécutives est souhaité, mais ces fréquences doivent être parfaitement synchronisées pour générer des pulses extrêmement courts : c’est le principe des technologies de laser femtoseconde.
Lasers continus vs lasers pulsés
Les lasers peuvent délivrer leur rayonnement de manière continue (constante dans le temps) ou pulsée. Certains lasers utilisant un milieu gazeux (ex : Hélium Néon : He/Ne) sont des lasers qui procurent une émission continue. Les lasers à excimères, les lasers femtoseconde ou encore le laser Nd :Yag utilisés en ophtalmolgie sont des lasers pulsés.
Avec les lasers pulsés, l’énergie délivrée peut être concentrée dans le temps : en d’autres termes, la puissance émise (énergie par unité de temps) peut être augmentée. Un laser qui émet 1 Joule en une seconde a une puissance de 1 Watt. Si ce Joule est émis sur une période de 10-6 secondes, la puissance générée est de 1000 Watts. La période d’émission correspond à la durée qui sépare deux pulses. En fonction des applications (médicales ou industrielles) la puissance émise par les lasers excimères varie entre 0.50 et 50 Watt.
La puissance crête est égale à l’énergie délivrée par le pulse sur la durée du pulse lui-même. La durée d’émission des pulses émis par les lasers femtoseconde est de quelque centaines de femtoseconde (une femto seconde est égale à 10-15 secondes) : cette durée est extrêmement brève au regard de la période (durée séparant deux pulses, de l’ordre de 5. 10-6 secondes avec un laser à 200 KHz comme le Wavelight FS 200). L’énergie délivrée dans un pulse est faible, de l’ordre d’une micro joule (10-6 J), mais le temps extrêmement bref de l’émission garantit une puissance crête très élevée, à même d’ioniser la matière en vainquant la force reliant les électrons aux noyaux atomiques (voir ici pour plus d’informations chiffrées sur les ordres de grandeur)

Bonjour,
Vos explications sont très claires
Avec mes remerciements
Dr Yen BUI