Le trajet des rayons dans l’oeil
Le trajet des rayons lumineux dans l’oeil
Cette page concerne l’oeil vis à vis des lois de l’optique géométrique et ses rayons lumineux. Nous négligerons pour le moment les effets de la diffraction, et considèreront que les rayons peuvent se couper en un point (stigmatisme rigoureux). Nous avons souligné précédemment, pour que l’image rétinienne soit nette, un pré requis fondamental est que les rayons émis par les sources ponctuelles élémentaires et captés par l’œil soient focalisés dans le plan du tissu rétinien photosensible. Nous avons vu que quand les rayons étaient focalisés en dehors de ce plan, ils formaient sur la rétine une tache d’éclairement en forme de disque, d’autant plus large que les rayons étaient défocalisés.
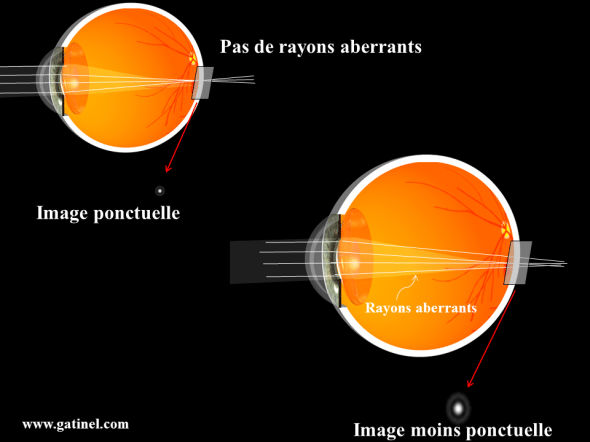
Envisageons une situation intermédiaire : que se passe-t ’il quand seule une partie des rayons captés par l’œil focalise dans le plan rétinien, et donc que l’autre partie focalise en dehors ? Cette question est pleinement du ressort de l’aberrométrie, qui vise à étudier de manière exhaustive le trajet de l’ensemble des rayons captés par la pupille pour en déduire la PSF. Les rayons qui ne convergent pas dans le plan de la rétine sont des rayons dits « aberrants » ou « aberrés ». Quand tout ou partie des rayons lumineux n’est pas focalisée en un même point, on parle plus généralement d’aberrations optiques. C’est l’une des spécificités de l’aberrométrie, qui tient compte de tous les rayons collectés par l’oeil : ceux qui passent par ou au voisinage immédiat du centre de la pupille, mais aussi ceux qui passent plus à distance, près des bords, sans oublier ceux qui passent « au contact » de ces bords (ceux-là sont « diffractés », il est en fait plus commode en aberrométrie de considérer le flux de lumière incident comme un « front d’onde lumineux », plutôt qu’un bouquet de rayons).
Si une proportion suffisante des rayons captés se coupent dans le plan rétinien, la plupart des détails présents dans le motif observés peuvent être préservés au sein de l’image rétinienne, car la tache d’éclairement rétinien ne s’étale pas trop …Cependant, le contraste de l’image sera affecté ! L’aberrométrie permet ainsi non seulement de prédire l’acuité visuelle d’un œil, mais aussi la manière dont s’atténue le contraste de l’image rétinienne. L’aberrométrie permet aussi d’étudier certaines situations où l’œil présente un problème optique susceptible d’induire des images rétiniennes particulières, (ex : vision de halos nocturnes, ou d’images fantômes dédoublant certains contours lumineux…).
Il est temps de signaler que pour des raisons de simplicité, nous avons parlé de blanc, de noir, de gris, etc.. et comme au temps des débuts du cinéma et de la télévision, occulté l’aspect polychromatique de notre monde environnant. Les principes esquissés ici s’appliquent également aux différentes radiations colorées, au prix de petits aménagements de calcul qu’il est tout à fait possible de négliger à ce stade. Gardons simplement à l’esprit que ce qui est vrai pour un rayon « rouge », n’est pas toujours tout à fait exact pour un rayon « bleu ». Les rayons « bleus » ont par exemple tendance à former des taches focales plus petites que les rayons « rouges » (car comme la longueur d’onde des radiations bleue est plus petite, elles diffractent moins). C’est pour cela que l’on peut graver un disque « blu ray » de manière plus fine (le disque est lu avec une « pointe fine de lumière laser bleue ») et qu’il comporte plus d’information qu’un DVD (lu par une plus large « pointe de lumière laser rouge »).
En s’attardant sur la caractérisation des images et sur l’aspect colorimétrique de la lumière, et de certaines caractéristiques comme la longueur d’onde, nous nous sommes à nouveau éloignés des rivages de l’optique géométrique, qu’il est à présent temps de regagner définitivement, pour se pencher plus attentivement sur la manière dont les rayons lumineux captés se dirigent dans l’œil. Ainsi, dans tout ce qui suivra, nous assimilerons l’information lumineuse à un trajet de rayons, omettrons l’aspect ondulatoire de la lumière, et arpenterons un monde où les rayons peuvent se couper en un point : un monde ou le stigmatisme rigoureux est possible.
La réfraction de l’œil
Pour que les rayons lumineux (quelle que soient leur « couleur propre ») ne poursuivent pas le trajet parallèle ou divergent, mais se « mettent à converger » vers la rétine, il faut que quelque chose en infléchisse le trajet, et les fasse « basculer » en direction de la rétine centrale. L’œil humain (comme celui de la plupart des mammifères et animaux terrestres et marins) dispose pour cela de deux tissus remarquables à plus d’un titre : la cornée et le cristallin.
En traversant la cornée puis le cristallin, les rayons subissent des déflexions que l’on regroupe sous le terme de réfraction: on dit que ces rayons sont réfractés. De nombreux savants se sont intéressés à l’étude des lois qui gouvernent le trajet des rayons lumineux au sein des structures optiques naturelles ou artificielles : les lois de la réfraction furent établies par Snell et Descartes. Le cristallin de l’œil humain est souple, (du moins avant l’instauration de la presbytie, vers la quarantaine) et permet à l’œil en se déformant (en bombant) de former une image nette même quand des rayons même fortement divergents arrivent au contact de l’œil. Ces rayons sont fortement divergents, car émis par des sources rapprochées – comme les pixels de l’écran de votre ordinateur vis-à-vis de vos yeux). Ce mécanisme est appelé accommodation du cristallin.
Quand l’œil (le cristallin) n’est plus à même de se déformer suffisamment pour que les rayons convergent suffisamment (l’accommodation du cristallin devient insuffisante), il faut recourir à une « lentille » externe, c’est-à-dire un verre de lunette convexe, sorte de « loupe » qui fournit le supplément de convergence supplémentaire. L’utilisation de ces lois de la réfraction permet de comprendre comment les rayons lumineux sont déviés, et servent à la mise au point de formules plus générales (nombreuses en optique géométrique, mais dont la plus importante est la formule dite de « vergence »).
Ces formules visent en grande partie à répondre à une question simple : où se forme l’image après sa réfraction par les tissus oculaires ? Ce qui intéresse surtout le clinicien, c’est de savoir si ces rayons convergent dans le plan rétinien… où en dehors. En plus de cette curiosité légitime, connaître les lois qui gouvernent le trajet des rayons lumineux permet également de calculer la puissance optique (la capacité à faire diverger les rayons lumineux) d’un cristallin artificiel, qui une fois inséré en remplacement d’un cristallin opacifié (opération de la cataracte).
Plus couramment, ces mêmes formules sont utiles pour déterminer la courbure d’un verre de lunettes destiné à corriger la myopie, l’hypermétropie, l’astigmatisme, et/ou la presbytie. Enfin, il peut être intéressant de connaître la taille de l’image sur la rétine, car de ses rapports avec la taille élémentaire des éléments photosensibles, on pourra déduire la finesse des détails qui seront « échantillonnés », et celle de ceux qui seront perdus… Il existe des formules simples qui permettent de calculer la taille des images formées par un système optique. Mais avant d’aborder ces formules au fil des pages du site, il est certainement plus important à ce stade d’en comprendre, la genèse, le rôle, et les liens.
La loi de la réfraction
Nous avons compris que la loi de la réfraction est un pilier de l’optique géométrique, dont découlent des formules largement utilisées pour prédire le trajet des rayons lumineux au travers des milieux optiques, et donc des tissus oculaires. La loi de la réfraction se déduit du principe dit de « moindre action » : il stipule simplement que pour aller d’un point à un autre, un rayon de lumière empruntera le chemin le plus bref en temps de parcours. Là encore, le rayon lumineux doit être compris comme une donnée abstraite, qui matérialiserait le trajet de particules de lumière (les photons), qui seraient émises dans la direction du rayon. On suppose qu’un photon émis dans une direction donnée dans un milieu homogène continue son chemin en ligne droite (c’est seulement lors de la détection du photon que l’on peut déduire le trajet qu’il a emprunté, car il n’est pas possible de « suivre » le trajet d’un photon).
Reprenons l’exemple d’une étoile source de lumière. De cette étoile nait et se propage un signal lumineux (ou des photons si l’on préfère considérer la lumière comme un flux de particules) qui se transmet dans l’espace environnant, à la vitesse de 300 000 Km secondes : pour réaliser ce que représente cette célérité, la lumière pourrait avoir effectué environ 7 tours de Terre depuis que vous avez lu le début de cette phrase, ou encore effectué le trajet jusqu’à la Lune. Pour faire 7 tours de Terre par seconde, la lumière doit voyager dans le vide (ou dans l’air). Dans l’eau, le temps pris pour effectuer ce même parcours serait d’environ 1,33 fois plus long… En effet, la lumière ralentit dans certains milieux par rapport à la vitesse, indépassable, qu’elle adopte dans le vide. Quel que soit le milieu traversé, la lumière met le temps le plus court pour aller d’un point à un autre : au sein d’un même milieu, la lumière ira donc en ligne droite pour relier deux points, car la ligne droite est la distance la plus courte entre deux points.
Le fait que la lumière emprunte systématiquement le chemin le plus court temporellement ne doit pas nous inciter à croire qu’il suffirait de relier deux points par un trait pour représenter la direction prise par le rayon. Cette méthode ne fonctionne plus quand les points sont chacun situés dans deux milieux différents (ex : air et eau). En effet, il ne faut pas confondre durée et distance ! Du moins, on peut entretenir cette confusion tant que le milieu traversé par la lumière ne change pas, et qu’il est optiquement « homogène » (le point de départ et le point d’arrivée sont tous deux situés dans l’air, ou dans l’eau, ou dans le verre, et le signal lumineux demeure dans le même milieu pendant l’intégralité de son trajet).
Quand la lumière passe d’un milieu à un autre, le trajet le plus court (en temps) n’est plus forcément le plus court (en distance). On peut deviner la cause de ce paradoxe apparent : elle est que la vitesse de la lumière varie selon le milieu emprunté. La lumière ne va jamais plus vite que dans le vide, mais sa vitesse chute dans certains milieux, « optiquement denses ».
Dans l’œil par exemple, la vitesse de la lumière est comparable à celle qu’elle aurait dans l’eau : elle y diminue d’un tiers environ L’étude du trajet de la lumière au sein des milieux requiert que l’on puisse quantifier précisément au moyen d’un chiffre appelé « indice de réfraction » (et désigné par la lettre « n ») la manière dont un matériau « freine » la lumière (on parle ici bien entendu de matériaux transparents et non purement réfléchissants, qui se contentent de renvoyer la lumière, comme les miroirs). La vitesse de la lumière dans le vide sert de référence.
Si un milieu à un indice de 1,5 (n=1,5), cela veut dire que la vitesse de la lumière dans le vide est 1,5 fois supérieure à celle qu’elle prend dans ledit milieu. Une conséquence directe de ce ralentissement est que quand la lumière a parcouru 1,5 millimètre dans le vide, elle n’a parcouru que 1 millimètre dans le milieu. Le produit de la distance physique par l’indice de réfraction s’appelle le chemin optique.
Pour appréhender ce concept, imaginons le trajet parcouru par une particule de lumière le long d’un rayon dans un milieu optique (n>1) pendant une durée déterminée : comme la lumière ralenti (n>1), la distance parcourue est moindre que si la particule avait cheminé dans le vide. Le chemin optique exprime correspond à la distance physique qu’aurait parcouru dans la lumière vide pendant la même durée de trajet.
Chemin plus court, ou chemin plus bref?
Pour prédire la manière dont la lumière se propage entre deux points situés chacun dans deux milieux différents, en franchissant l’interface qui sépare ces milieux, on peut et on doit appliquer le principe de Fermat : la lumière emprunte le trajet (temporellement) le plus court entre deux points. A ce stade, il est important de bien comprendre que derrière la simplicité apparente du principe du chemin le plus bref, se dissimulent des questions plus profondes voire philosophiques : on pourrait supposer que la lumière émise par le point situé dans le premier milieu pourrait emprunter n’importe quel chemin a priori pour aller au point situé dans le second milieu… ou du moins essayer tous les chemins possibles avant de déterminer celui qu est le plus court.
Comment fait le rayon, où la particule de lumière dont le rayon matérialise la direction de propagation, pour connaître d’emblée ce chemin le plus court ? Les réponses à ces questions sont apportées par la théorie de l’électrodynamique quantique, et popularisées par le physicien Richard Feynman. En ce qui concerne la quête d’une loi permettant de prédire le trajet adopté par un rayon réfracté, il faut raisonner de manière finaliste : en utilisant le principe de Fermat, qui postule que ce chemin sera le plus « rapide », le plus court en temps, on doit pouvoir relier n’importe quel point d’un premier milieu (point n°1) (P1), avec n’importe quel point d’un second milieu (point n°2) (P2) par un chemin unique, de temps minimal.
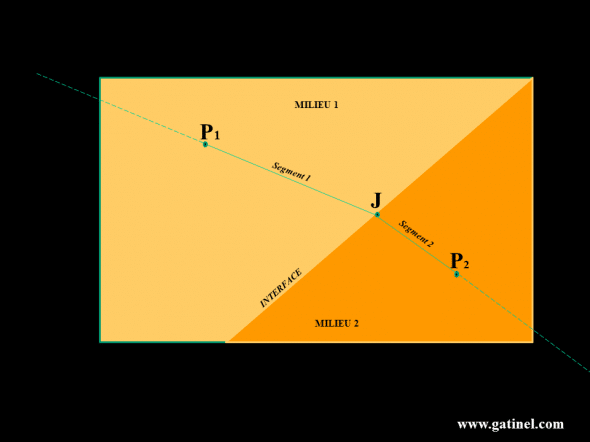
- Le milieu 1 et le milieu deux sont séparés par une interface rectiligne, mais n’ont pas le même indice de réfraction: la vitesse de la lumière n’est pas la même dans le milieu 1 que dans le milieu 2. Pour aller du point 1, situé dans le milieu 1, au point 2, situé dans le milieu 2, il existe un chemin de temps de parcours minimum, constitué de deux segments reliés par un point J situé à la jonction (interface) des milieux. Tout rayon passant par le point 1 et dirigé selon le segment 1 emprunte ensuite le trajet du segment 2 dans le milieu 2. Quel que soit le point situé sur la droite (P1J), le trajet qu’empruntera un rayon dirigé et passant par J passe par le point n°2.
Le trajet sera constitué de deux segments, puisque la lumière se propage en ligne droite tant qu’elle reste dans un milieu homogène. Le premier segment ira du point n°1 à un point situé à jonction des deux milieux (le point J, situé le long de l’interface), et le second segment ira de ce point J au point n°2. Comme au sein d’un même milieu, le temps minimum pour aller d’un point un l’autre est la ligne droite, on en déduit qu’un rayon de lumière qui passerait par le point n°1 et contenant le premier segment (et donc par le point J) continuera son chemin dans le second milieu en passant par le point n°2. Peu importe la position de la source à l’origine du rayon En optique physiologique, on cherche à déterminer le trajet de rayons issus d’une source au sein des milieux oculaires, dont on connait la géométrie, l’indice de réfraction… On ne cherche pas véritablement à déterminer le trajet le plus court entre deux points, mais comme nous allons le voir, la résolution de ce problème fournit une loi générale (loi de la réfraction) qui permet d’établir le trajet emprunté par un rayon lumineux réfracté au sein d’une interface.
Une analogie avec le « dilemme du maître-nageur » résume de manière imagée la problématique du chemin le plus bref.
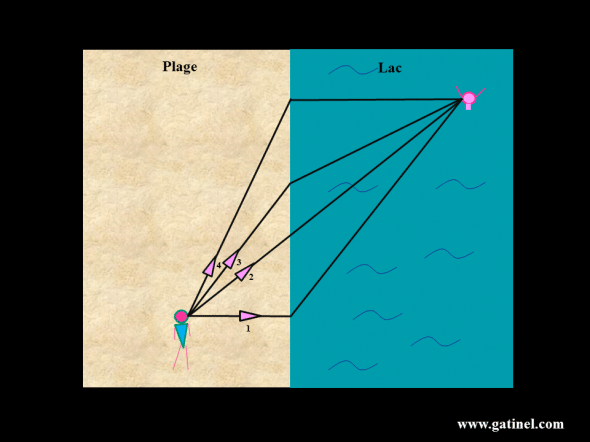
- Pour secourir au plus vite le baigneur en difficulté, le maitre nageur, qui ne peut nager aussi vite (ex: 5 km/h) qu’il courre (ex: 15 km/h), doit choisir le chemin le plus « bref » (celui qui requiert le temps de parcours minimal). Si l’on s’en tient à la distance physique entre le MN et le baigneur, le chemin 2 est le plus court géométriquement; il est a priori plus bref que le chemin 1 car la distance de nage y est significativement plus longue que la distance de course, et a priori que le chemin 4, dont la distance de nage est plus courte, mais la course beaucoup plus longue . Cependant, le temps du chemin 3 pourrait certainement être plus bref, car même si la course est un peu plus longue, la nage y est plus courte et ceci procure un gain de temps significatif! Pour résoudre le problème et trouver le parcours dont le temps est minimal, il faut tenir compte des distances, et de la vitesse de déplacement dans les milieux parcourus (ici la plage, et l’eau du lac). Le temps mis pour parcourir une distance dans un milieu est égal au rapport entre la distance et la vitesse.
- On appelle « chemin optique » la distance dans le milieu multipliée par l’indice de réfraction du milieu – l’indice est une fonction inverse de la vitesse de déplacement de la lumière,). Le chemin optique exprime en fait une « durée temporelle » ! En partant du principe de Fermat (le temps parcouru par la lumière entre deux points est le plus bref), la mise en équation de cette situation mène à la loi de la réfraction dite de Snell-Descartes.
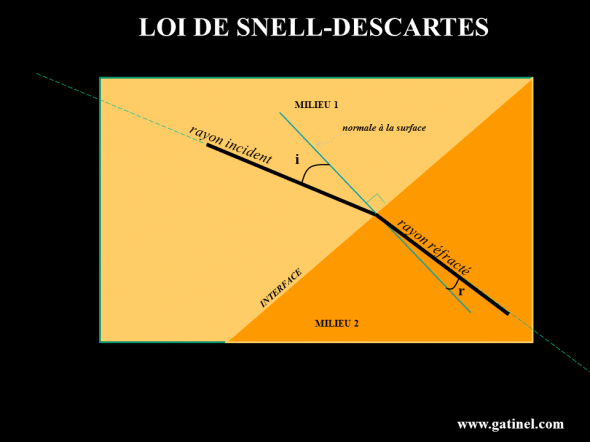
Supposons donc un maitre-nageur sauveteur qui aperçoit depuis les berges d’un lac un malheureux nageur imprudent sur le point de se noyer. Sachant que pour le rejoindre le maitre-nageur devra successivement courir puis nager, et qu’il nage plus vite qu’il ne court, quel est le trajet « optimal » qu’il devra emprunter ? C’est à cette question, transposée au domaine des « rayons lumineux », qu’ont offert une réponse claire Snell et Descartes (plus d’informations sur cette loi et ses liens avec la propagation de la lumière), au terme de série d’observations minutieuses et de montages empiriques. sin(r) = (ni / nr) x sin(i)
Le sinus de l’angle de réfraction est égal au rapport entre les indices de réfraction multiplié par le sinus de l’angle d’incidence. Ces angles sont formés entre le rayon et la droite perpendiculaire à l’interface au point de contact. Cette formule comporte un outil mathématique appelé « sinus », qui est un rapport entre deux longueurs reliées entre elles par un angle. Pour les petits angles, le sinus de l’angle est égal à l’ange lui-même. Cette loi fournit un renseignement précieux : seul l’angle du rayon incident avec la surface et le rapport des indices de réfraction conditionne la valeur de l’angle du rayon réfracté. Ce qui compte, c’est l’angle que fait le rayon avec l’interface et pas la position de la source à l’origine du rayon. Cette loi fait intervenir logiquement la vitesse de la lumière dans les milieux considérés, (exprimée au travers de la valeur des indices de réfraction).
Au-delà du formalisme mathématique, ce que cette loi nous enseigne, c’est que si l’on connait la vitesse de déplacement d’un rayon de lumière dans les milieux qu’elle emprunte, et sa direction incidente (l’angle que font les rayons quand ils rencontrent l’interface avec le nouveau milieu), alors on peut calculer l’angle sous lequel il est dévié, c’est à dire « réfracté ». Ensuite, tant que le rayon reste dans le même milieu (même indice de réfraction), sont trajet s’effectue en ligne droite, en vertu du principe d’économie en tant de transport. S’il rencontre un nouveau milieu, il suffit de déterminer l’angle qu’il forme avec l’interface qui sépare celui-ci, et connaître son indice de réfraction : on peut appliquer à nouveau la loi de Snell Descartes. Cette démarche, appliquée de rayon en rayon et d’interface en interface s’appelle le « lancer de rayons » ou « ray tracing ». Fastidieux à la main, il est devenu courant grâce au calcul informatique accompli par les ordinateurs où des logiciels dédiés permettent de simuler le trajet de la lumière au sein de modèles optiques.
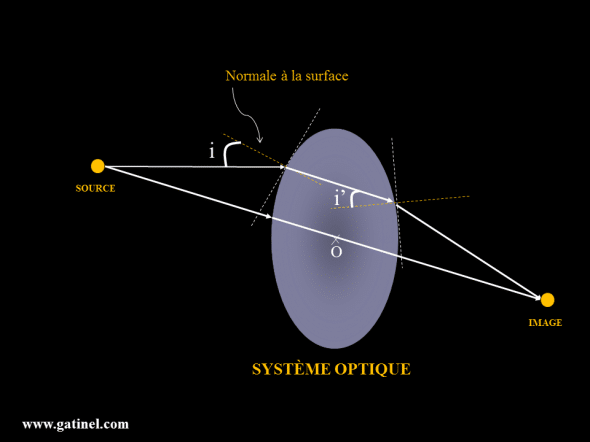
- Les lois de la réfraction permettent de tracer le trajet des rayons au travers d’un système optique dont on connait la géométrie (il faut connaitre leur courbure locale, pour positionner la normale à la surface, déterminer l’angle d’incidence, et calculer l’angle de réfraction grâce à la loi de la réfraction). Ceci peut être utile pour déterminer la position du plant de l’image nette d’un objet source: on trace plusieurs rayons, et on observe où ils se coupent. On peut aussi utiliser certaines formules simplifiées (ou le fait que les rayons qui passent par le centre du système optique ne sont pas déviés), qui permettent de déterminer la position où les rayons émis par une source dont on connait la distance avec le système optique seront focalisés (position de l’image).
Le ray tracing est utilisé pour mettre au point des solutions optiques, qui vont des verres de lunettes aux lentilles oculaires, aux implants, etc. On modélise l’œil et la solution testée, et on calcule avec un ordinateur le trajet des rayons quand ils se propagent au sein de l’œil et de l’équipement testé. Ces simulations permettent de définir une géométrie optimale de l’équipement optique. Quand on cherche à simplement prédire la position d’une image formée par l’œil (est-elle dans le plan de la rétine ?), et que l’on a pas recours à un logiciel de ray tracing, on peut également utiliser une approximation appelée formule de vergence, qui découle de la loi de Snell Descartes. La formule de vergence ne nécessite pas que l’on calcule le trajet de rayons particuliers : elle fait simplement appel à la position de l’objet vis-à-vis du système optique, et de la distance à laquelle ce système focalise les rayons (l’inverse de cette distance focale est appelée vergence).
La formule de vergence est une manière efficace et simple de calculer la position d’une image après réfraction des rayons par le sommet d’une lentille ou d’un dioptre (c’est à dire le plan où si on plaçait un écran, l’image formée serait la plus nette car égal au plan d’intersection des rayons réfractés).
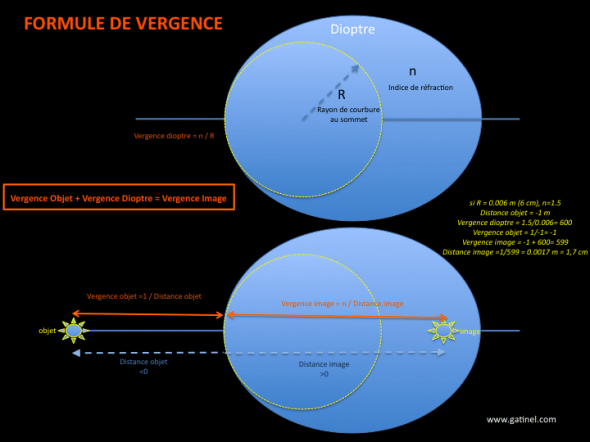
- Un dioptre placé dans l’air (n=1) possède un indice de réfraction et une courbure apicale (au sommet, le long de l’axe optique) qui permettent de calculer sa vergence. Si l’on connaît la position de l’objet vis à vis du sommet du dioptre, on peut alors calculer la position de l’image grâce à la formule de vergence, qui stipule que la somme de la vergence de l’objet (inverse de la distance dans l’air) ajoutée à la vergence du dioptre est égale à la distance de l’image. Par convention, les distances « vers la droite » sont de signe positif.
C’est donc du principe de Fermat, celui de la moindre action que découle la loi la plus enseignée de l’optique géométrique, la loi de la réfraction, ou loi des sinus. Si le principe de Fermat est la clé de voûte des théories optiques qui s’attachent à décrire le trajet de la lumière dans des conditions classiques ; la loi des sinus forme le pilier principal de l’échafaudage des formules théoriques que l’on utilise couramment en optique géométrique, comme la formule de vergence.

Laisser un commentaire