6. Paraxial optical power of the cornea
This page is dedicated to the study of thick lens formulas that characterize the cornea’s paraxial properties. These formulas allow the calculation of the power of the cornea’s anterior and posterior surfaces and of the total cornea.
The determination of the location of the principal planes of the cornea will also be discussed. At the end of this page, an interactive calculator allows you to calculate all these values.
What are we looking for?
We want to determine a paraxial model of the cornea, which involves determining the position of the principal planes and the focal distances, as for a thick lens. The paraxial optical power or vergence of the cornea depends on its front and back surfaces’ curvature and thickness.
In this context, it is necessary to know the values of the paraxial radii of curvature of the anterior face and the posterior face of the cornea and its thickness. These values can be obtained thanks to measurements in OCT, in corneal topography, and measurements carried out by certain biometers.
What do we need?
The topography (Scheimpflug or OCT) of the cornea and certain biometers allow the measurement of the apical curvatures of the anterior and posterior corneal surfaces (Rca and Rcp, respectively) and of the corneal thickness.
The anterior surface of the cornea is in contact with air, while the posterior surface of the cornea is in contact with the aqueous humor. It is necessary to know the values of the refractive indices of these media (n0 and na) and the refractive index of the corneal stroma (ns).
Paraxial formulas
Using such information, we can determine the vergence (paraxial optical power) of the anterior and posterior surfaces and the entire cornea (combined effect of the anterior and posterior surfaces). Finally, we can determine the positions of the principal planes.
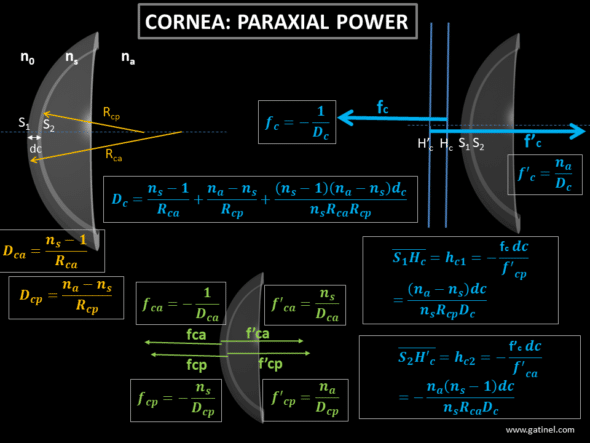
All the necessary formulas are gathered for these calculations are shown in this illustration:
This figure makes it possible to calculate for the anterior surface, the posterior surface, and the cornea assimilated to a thick lens:
-the paraxial power,
-the object focal distance,
-the image focal length,
– the position of the principal planes of the cornea (thick lens).
Numerical example
We consider the value of the refractive index of the corneal stroma (ns = 1.376, and of the aqueous humor (na = 1.337)
The anterior curvature has a radius Rca = 7.8 mm.
The posterior curvature has a radius Rcp = 6.5 mm
The central corneal thickness is dc = S1S2 = 0.55 mm
Calculation of the power of the anterior surface of the cornea in air:
Dca = (nc – 1) / Rca = (1.376 -1) /0.0078 = 48.21 D
Focal distances of the anterior surface:
The object focal length is given by fca = -1 / 48.21 = -0.02074 m
The image focal length is given by f’ca = 1.376 / 48.21 = 0.02854 m
Calculation of the power of the posterior surface side of the cornea:
Dcp = (na – ns) / Rcp = (1.337 -1.376) /0.0065 = -6.0 D the steeper the posterior surface (Rcp decreases), the more negative (divergent) its optical power.
Focal distances of the posterior surface:
Object focal length fcp = -1.376 / -6.0 m = 0.2293 m
The image focal length f’cp = 1.337 / -6.0 m = -0.2228 m
Cornea: thick lens equivalent
The next step is to calculate the power of the centered system equivalent to the cornea (Dc), taking into account the thickness of the cornea at the center (distance between the anterior and the posterior surface).
Power of the centered system equivalent to the cornea (Dc)
For this, we use Gullstrand’s formula, which concerns « thick » systems: we subtract from the sum of the power terms the product of the thickness by the front and back powers divided by the refractive index of the stroma.
Dc = Da + Dp – dc (DaDp) /nc = 48.21 -6.15 –0.00055 x 48.21x-6.15 / 1.376 = 42.32D
Focal distances of the cornea:
The object focal length of the cornea is equal to fc = -1 / Dc = -1 / 42.32 m = -0.02362 m
The corneal image focal length is equal to f’c = 1.337 / Dc = 1.337 / 42.32 = 0.03158 m
Position of the principal planes and points (intersection of the planes with the optical axis) of the cornea.
(a page is devoted to the explanations and calculation of the position of the principal planes of a paraxial system).
The distance between principal object plane Hc and the vertex of the cornea S1 is:
S1Hc = dc x fc / fcp = 0.55 x (-23.62) / (22.93) = – 0.0567 mm
The distance between the principal image plane H’co and the vertex of the cornea S2 is:
S2H’c = -dc x f’c / f’ca = -0.55 x (31.58) / (28.54) = – 0.6085 mm
The negative sign of the distances corresponds to a position of the principal object plane located in front of the cornea (58.3 microns before S1). The position of the principal image plane is also located at 0.55-0.6085 = 0.0585mm, approximately 60 microns in front of the front surface (S1).
The distance between the principal planes of the cornea (1.8 microns) is clinically negligible.
In a thick lens paraxial model of the « pseudophakic » eye, which would associate cornea and IOL, the effective position of the IOL corresponds to the distance between the principal image plane of the cornea and the principal object plane of the implant.
Keratometric power of the cornea
This approximation corresponds to the use of a « minored » corneal refractive index – or keratometric index (nk), used on keratometers and in topograph software to calculate the keratometric power map (axial or tangential) in diopters. The interest of this approximation was related to the inability to measure the posterior surface of the cornea easily in clinical practice. It can provide a sufficiently precise estimate of the keratometric power in diopters for most current applications.
However, it is only valid for corneas where the effect of posterior curvature relative to the anterior surface power does not differ too much from the « average. »
For example, if we measure a curvature radius value of 8.5 mm (flat cornea, encountered after myopic LASIK or myopic PKR), with an unaltered posterior curvature value (6.5 mm), the power calculation paraxial using the previous equations gives the following value: Dc = 38.34 D. Using the commonly accepted value of a keratometric index of nk=1.3375, we obtain Dk = 39.71.
This discrepancy can have significant clinical consequences. It is therefore not recommended to rely on this approximation (cornea = spherical dioptre of curvature Rca with reduced index nk) after refractive surgery to perform IOL power calculation, especially since the other inaccuracies in the measurement of keratometry tend after refractive surgery to overestimate the paraxial power of the cornea … which induces an underestimation of the power of the implant to be placed and risks inducing hyperopia after cataract surgery.
Interactive Calculator for the paraxial optical power of the cornea
This spreadsheet is used to calculate the different variables mentioned on this page, which concern the thick cornea’s paraxial optical power.
One can also use this approach to characterize the paraxial properties of IOLs.

A fair deal of linear matrix calculations applied to the human eye can be found in the papers of Evans and Rubin (ex ; Linear optics of the eye and optical systems), in BMJ Open Ophthalmology:
This is the most complete analysis that I’ve found for the cornea treated as a thick lens.
Where can I find this analysis in a matrix optics form?; specifically for the cornea.