Nyquist (théorème de)
Le théorème de Nyquist concerne les propriétés d’échantillonnage d’un signal. Il conditionne en partie l’acuité visuelle théorique de l’œil humain. Dans les conditions idéales (mais non physiologiques) où l’œil présenterait un taux nul d’aberrations optiques de haut degré, la limite imposée par la diffraction impose que le diamètre de la tâche d’éclairement rétinien soit de un peu moins de 2 microns pour une pupille de 6 mm, soit à peu près la distance entre les centres de deux cônes adjacents dans la fovéa. Cependant, si l’on souhaite séparer deux points avec un écart angulaire minimal, il ne suffit pas que les images de chaque point « tombent » chacune sur un cône différent et que ces deux cônes soit adjacents (dans ces conditions, l’écart entre les tâches d’Airy satisfait le critère de Rayleigh). Ce type de séparation aboutirait à voir un point source unique. Il faut que l’image de chaque point source stimule chacune un cône, mais que ces deux cônes séparés par un cône non stimulé.
Imaginons un motif de points sources, écartés d’une distance angulaire constante égale à l’angle de résolution minimal de l’œil (dans les conditions idéales citées plus haut). Cet ensemble de point est réparti selon une certaine « fréquence » (nombre de points par unité de distance). Dans ces conditions, la fréquence d’échantillonnage de la rétine fovéolaire doit au minimum être égale au double de la « fréquence » contenue dans le signal. Ce rapport du simple au double entre la fréquence du signal et celle de l’échantillonnage rétinien est le fondement du théorème de Nyquist – Shannon, qui stipule que pour échantillonner correctement un signal, il faut une fréquence d’échantillonnage égale au double de la fréquence contenue dans le signal.
La lettre E est constituée par un réseau de barres horizontales alternativement brillantes et sombres (oublions la barre verticale de cette lettre). Le motif élémentaire de cette lettre est lui-même constitué d’une paire de barres (une barre noire, une barre blanche), qui se répète deux fois et demi. Cette paire est résolue si l’image rétinienne de l’espacement entre ces barres constitutives correspond au moins à l’espacement entre deux cônes. La plus part des lettres constitutives d’une série d’optotypes peuvent être vues comme l’agencement de « paires » de barres plus ou moins longues, et d’orientation variable.
Pour généraliser ce concept à l’ensemble des motifs visuels, on peut remplacer notre paire de barres par un cycle comprenant une portion « brillante », et une portion « sombre » mais où, à la différence du cycle issu des barres du E, la transition entre le blanc et le noir n’est pas abrupte. Dans ce cycle, le « raccord » est progressif entre la partie la plus brillante- la région où la luminance est plus forte – et la partie la plus sombre – la région où la luminance est plus faible ». Le cycle le plus fin que la rétine peut échantillonner couvre deux fois la distance minimale entre deux cônes fovéolaires. Cette distance est celle qui sépare la région la plus claire de la région la plus sombre d’un « cycle ».Quand la rétine doit échantillonner des cycles plus fins que la résolution rétinienne ne permet d’échantillonner, un phénomène de perception erronée dénommé « aliasing » peut survenir.
Considérons un signal élémentaire comme celui d’une fréquence spatiale (en cycles par degré). Chaque cycle, constitué d’une paire de bandes de luminance (une sombre, une claire) doit être convenablement échantillonné pour être perçu; la bande sombre et la bande claire du cycle doivent se projeter sur un photorécepteur distinct. Quand ces photorécepteurs (cônes) sont adjacents, on atteint la limite d’échantillonnage.
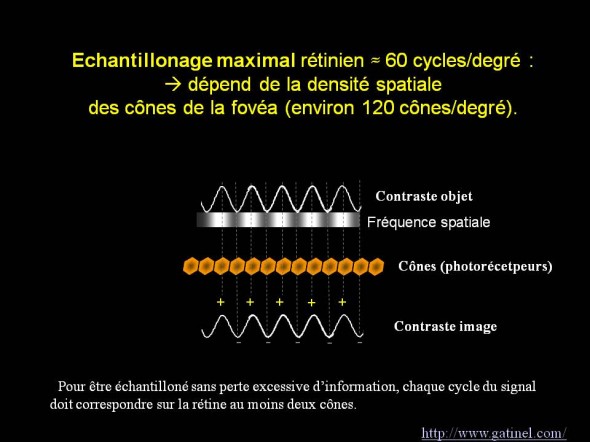
Echantillonnage d'une fréquence spatiale par les cônes de la fovéola à la limite (théorème de Nyquist)
Quand le signal est « trop fin » (supérieur à la limite de Nyquist), l’échantillonnage résulte en une perte d’information, ou la perception de motifs « erronés »: ce phénomène est appelé « aliasing ».
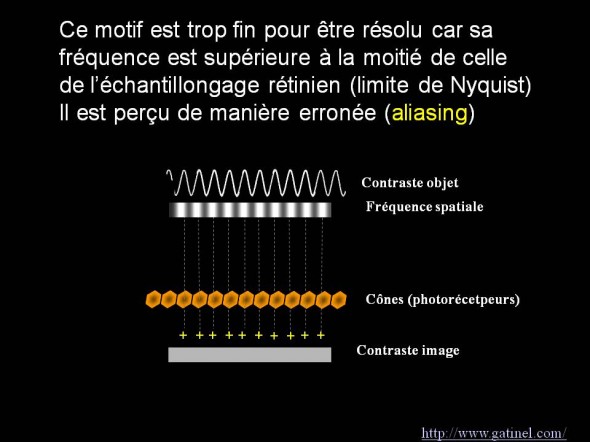
Phénomène d'aliasing, lié un échantillonnage insuffisant : dans cet exemple, le signal n'est perçu que comme une bande de luminance homogène.
En utilisant une longueur focale de 17 mm, on peut établir l’angle sous tendu par ce cycle : l’inverse de ce nombre nous fournit le nombre de de cycles qui « tiendraient » dans un angle de 1°. Les chiffres obtenus concernant les capacités d’échantillonnage limite de la mosaïque rétinienne varient entre 60 et 75 cycles par degré, selon que l’on choisit une distance inter-cône plus ou moins élevée. Le concept de « fréquences spatiales » est très important pour comprendre la Fonction de Transfert de Modulation (FTM ; Modulation Transfer Function) ; cette fonction fait correspondre contraste de l’image et contraste de l’objet: diffraction et aberrations optiques induisent une réduction (modulation) du contraste de l’image rétinienne vis à vis du contraste de l’objet.

Laisser un commentaire