Recueil du front d’onde
Le recueil du front d’onde préside à la réalisation d’un examen aberrométrique. La qualité optique de l’œil est très corrélée à l’existence de déphasages (différences de chemin optique) au sein du front d’onde. Les applications du recueil du front d’onde concernent principalement l’étude de certains symptômes visuels, dont on soupçonne l’origine d’être optique. En chirurgie réfractive, l’étude préopératoire des aberrations optiques permettra de déterminer l’intérêt d’un traitement personnalisé et d’en programmer la délivrance en guidant les tirs du laser.
Analyse du front d’onde en aberrométrie
L’analyse des aberrations optiques de l’œil repose sur les travaux de Hartmann et Tscherning au 19e siècle, qui ont donné naissance à deux catégories principales d’analyseurs de front d’ondes.
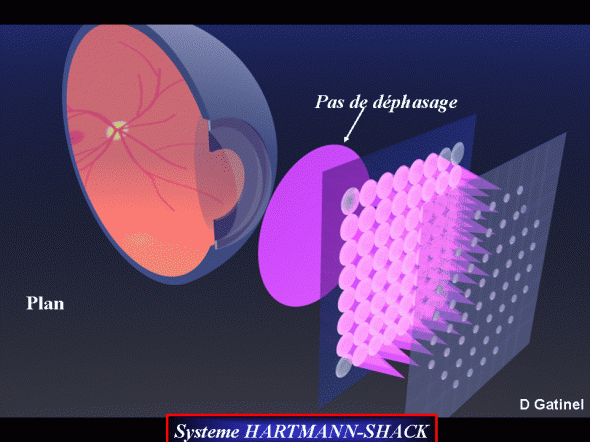
Etude du front d’ondes réfléchi : systèmes de type Hartmann-Schack
Principes du recueil du front d’onde
De façon schématique, les principales étapes permettant l’analyse du front d’ondes sont :
-émission d’un rayon laser incident centré sur la fovéa,
-recueil du signal réfléchi à la sortie de l’œil par une micro-réseau de lentilles,
-focalisation sur un capteur numérique du front d’ondes par chacune des lentilles du faisceau (le front d’ondes est ainsi « fragmenté » en plusieurs portions contiguës),
-mesure de la déviation du faisceau de chaque lentille par rapport à la position de référence (qui correspondrait à une portion de front d’ondes plat). La déviation correspond à l’écart de la position occupée par le centroide (image formée par la microlentille sur le capteur CCD) avec celle de référence.
-calcul mathématique par intégration, afin d’obtenir une représentation tridimensionelle du front d’onde.
Exemple : recueil d’un front d’onde « idéal » avec un aberromètre Schack Hartman
Nous raisonnerons de manière simplifiée, et dans un contexte purement « monofocal ». Pour un œil » idéal », c’est-à-dire dépourvu de toute aberration optique monochromatique (système uniquement limité par la diffraction pour les points sources situés à l’infini), le front d’ondes émergent tel qu’il est mesuré par l’aberromètre à la sortie de la pupille d’entrée est plat.
Aucune déviation n’est détectée par le réseau de microlentilles, chaque portion de ce « front d’onde » idéal à la sortie de l’oeil étant parallèle au plan de la microlentille. Il n’y a pas de différence de chemin optique pour tous les points de la pupille.
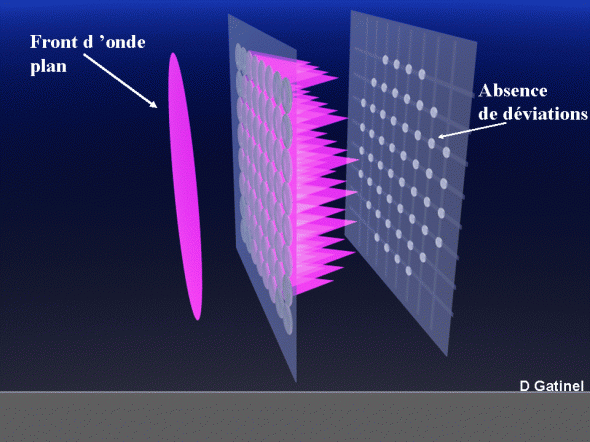
Si ce même front d’ondes était mesuré « à l’intérieur » de l’oeil, il serait parfaitement sphérique et centré sur la fovéa.
Etude du front d’ondes par imagerie rétinienne
-Analyseur de type Tscherning
-Lancer de rayons rétiniens : système Tracey (retinal ray tracing)
-Réfractométrie incidente ajustable (Ingoing adjustable refractometry)
Etude du front d’ondes par réfractométrie à balayage (système OPD scan)
Analyse du front d’ondes
Représentation du front d’onde
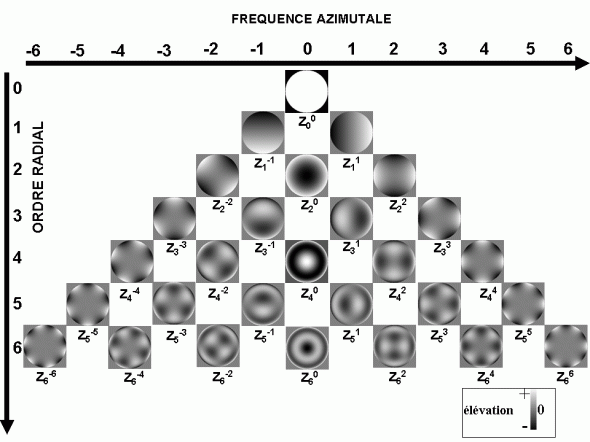
Le front d’onde est une construction théorique qui permet de représenter les différences de chemin optique (ou déphasage) sur l’ensemble de la pupille d’entrée (dans le cas de l’oeil, la pupille d’entrée correspond au pourtour de la pupille irienne). Pour être intelligible, l’analyse du front d’onde requiert que les aberrations qui s’y trouvent soient caractérisées (qualifiées) et quantifiées (taux). La représentation du front d’onde peut être effectuée par une décomposition en une somme de fonctions particulièrement intéressante dans ce contexte : les polynômes de Zernike. Les coefficients qui pondèrent ont une valeur proportionnelle à l’aberration optique qui leur correspond. Les premiers polynômes de Zernike s’interprètent aisément, car ils correspondent aux déphasages qu’infligent les aberrations optiques « classiques » comme le défocus, l’astigmatisme régulier, le coma, le trefoil, etc.
La base des polynômes de Zernike comprend théoriquement une infinité de polynômes; toutefois, le logiciel qui effectue la décomposition du front d’ondes travaille avec une « base tronquée » (c’est-à-dire un nombre limité de polynômes). Plus le nombre de polynômes choisis est faible, plus les calculs seront rapides, mais approchés (moins précis). De plus, le nombre de microlentilles de la matrice du capteur de l’aberromètre fixe le nombre maximal de points d’échantillonnage intervenant dans le calcul de décomposition du front d’ondes.
Principes de la décomposition en signaux élémentaires
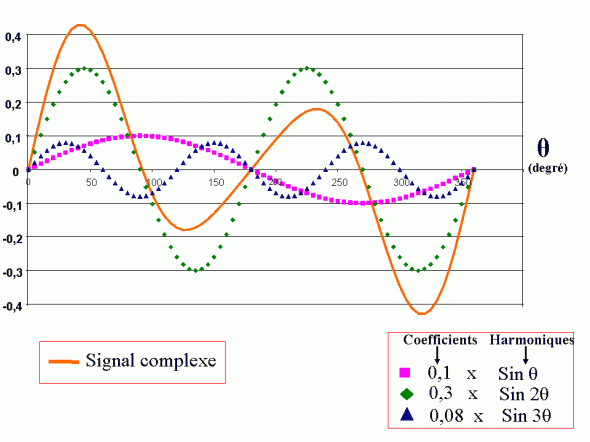
Principe de la décomposition d’un signal complexe en signaux élémentaires. Un signal complexe périodique peut être décomposé en harmoniques élémentaires affectées d’un coefficient particulier (décomposition spectrale). Dans cet exemple, trois harmoniques suffisent à la décomposition du signal complexe initial. L’addition de chacun de ces harmoniques permet de reconstituer le signal complexe : chaque harmonique est affectée d’un coefficient. Plus celui-ci est élevé, et plus son influence dans la forme du signal est importante (dans cet exemple, la forme globale du signal analysé est proche de l’harmonique (Sin 2θ). Ce type de décomposition en fonction sinusoïdale de fréquences croissantes (θ, 2θ, 3θ…) correspond à l’analyse de Fourier, qui vise à déterminer la valeur des coefficients à affecter à chacune des harmonique afin de reconstituer le signal initial par sommation. En général, plus le signal est complexe, et plus le nombre de signaux élémentaires nécessaires à sa description est élevé. Le principe utilisé pour la décomposition en polynômes de Zernike d’une surface telle que l’enveloppe d’un front d’onde est similaire. Chaque polynôme de Zernike peut être considéré comme une harmonique; l’analyse du front d’onde est effectuée en calculant la valeur du coefficient attribué à chacun des polynômes.
La transcription d’une surface d’onde recueillie en polynômes de Zernike s’apparente ainsi à la décomposition d’une note de musique en signaux harmoniques. En fonction du type d’instrument joué, l’intensité (nuance) de chaque harmonique sera différente et une valeur d’intensité pourra être attribuée à chaque signal harmonique. Au terme de ce processus, on aura décomposé la note initiale en une somme de signaux élémentaires affectés d’une valeur d’intensité sonore (amplitude du signal). Selon l’exactitude et le degré d’analyse pratiqué, il est possible de reconstituer secondairement plus ou moins fidèlement la note jouée à partir des informations fournies par le travail de décomposition initial. On pourra également extraire de la note une ou plusieurs harmoniques ; une note peut ainsi être « débarrassée » sélectivement d’harmoniques indésirables (pour une même note, le timbre d’un instrument de musique dépend de la composition harmonique de la note jouée).
Intérêt des polynômes de Zernike pour la description du front d’ondes
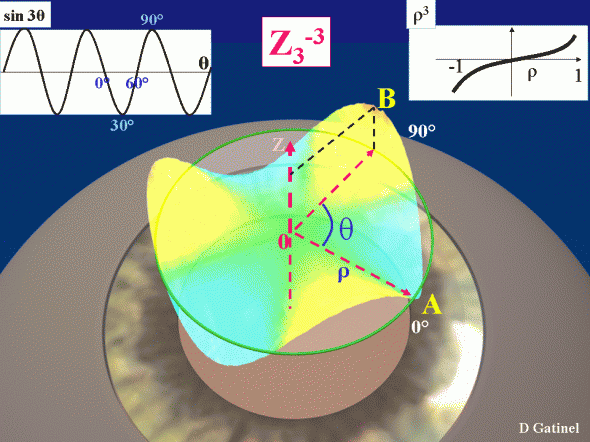
Représentation schématique du polynôme de Zernike (hors facteur de normalisation) correspondant à l’astigmatisme triangulaire (trefoil) Z3-3 sur le disque pupillaire normalisé (rayon égal à 1) matérialisé sur cette figure par un contour vert. Il est égal au produit d’une fonction polynomiale du rayon de degré 3 (ρ3 ) où ρ représente la distance du point considéré au centre, et d’une fonction trigonométrique de fréquence azimutale égale à 3 (sin3θ), où θ correspond à l’angle fait avec l’horizontale du méridien où est situé le point considéré.
Décomposition du front d’ondes en polynômes élémentaires
La décomposition mathématique d’un front d’ondes en polynômes de Zernike est un processus mathématique qui nécessite la normalisation du rayon de la pupille (la valeur du rayon de la pupille est supposée égale à 1 pour le calcul des coefficients). Toutefois, la distribution des polynômes et la valeur de chacun des coefficients varient en fonction du diamètre pupillaire obtenu lors du recueil du front d’ondes. Autrement dit, une variation de la valeur du diamètre pupillaire chez un même patient entre deux examens induit une variation dans la valeur des coefficients attribués aux différentes aberrations présentes au sein du front d’ondes étudié. En général, plus le diamètre pupillaire est grand, plus la valeur des coefficients attribués aux différents polynômes est élevée
De plus, les valeurs attribuées à chacun des coefficients RMS des polynômes utilisés pour l’analyse du front d’onde doivent être interprétés avec précaution. Si la qualité de la fonction visuelle dépend en partie du taux d’aberration présent au sein du front d’onde, elle n’est pas directement proportionnelle à ce taux et à la valeur des coefficients considérés séparément ou en groupe. Il existe en effet des compensations entre les aberrations optiques de différents degrés issues de la décomposition en polynômes de Zernike.
Interprétation du front d’ondes après décomposition en polynômes de Zernike
– A) Aberrations optiques en fonction de leur degré (ordre radial de la classification des polynômes de Zernike)
Il s’agit du tilt. Elles sont la conséquence d’un défaut d’inclinaison d’un ou plusieurs éléments constituant le système optique.
Il s’agit du défocus, et de l’astigmatisme. Ces aberrations correspondent aux amétropies sphéro-cylindriques paraxiales (sphère et cylindre). Le défocus correspond à une déformation parabolique du front d’onde avec symétrie de rotation. L’astigmatisme représente également une déformation parabolique du front d’onde, mais qui varie avec le méridien considéré et possède une symétrie axiale. Il correspond à la combinaison de deux surfaces en forme de selle, dont la résultante est une surface du même type mais dont l’orientation fournit l’axe de l’astigmatisme.
(voir Rubrique Astigmatisme sur le site)
Elles correspondent aux aberrations de type coma et trefoil (« trèfle »). Les polynômes qui les expriment ne présentent pas de symétrie de rotation ni de symétrie axiale. Elles traduisent un défaut d’alignement (décentrement) des éléments constituant le système optique. Leur taux augmente notablement après LASIK ou PKR, reflétant probablement une relative imperfection dans le centrage du traitement. Elles induisent un déphasage asymétrique prédominant sur les « bords » du front d’onde (augmentant avec la distance au centre de la pupille).
Il s’agit des aberrations de sphéricité. Les polynômes qui les expriment présentent tous une symétrie axiale, et pour certains, une symétrie de rotation. Elles augmentent avec le diamètre pupillaire et traduisent un déphasage des points du front d’ondes situés à la périphérie de la pupille d’entrée. Elles augmentent considérablement après LASIK et PKR conventionnelles, mais également et de façon moindre après chirurgie guidée par l’aberrométrie. Elles traduisent l’existence d’un resurfaçage suboptimal au niveau de la périphérie de la zone optique et/ou un diamètre insuffisant de cette dernière par rapport à celui de la pupille.
Selon le degré, elles présentent une symétrie axiale (degrés pairs) ou non (degrés impairs). Elles traduisent l’existence d’imperfections optiques multiples non systématisées qui exercent un effet particulier au niveau des bords du front d’onde.. Elles ont en général une faible incidence sur la fonction visuelle sauf quand leur taux est particulièrement élevé (comme au décours d’une cicatrisation cornéenne irrégulière, d’une chirurgie incisionnelle ou d’une kératoplastie transfixiante).
-B) Application à l’interprétation du front d’ondes
-en cas d’amétropie sphérique importante, le front d’onde aura une forme globalement parabolique ! cette parabole peut être approximée par une couple sphérique en première approximation; elle est centrée sur le punctum remotum de l’oeil amétrope.
-en cas d’amétropie myopique, le sommet de la parabole est dirigé vers l’arrière (le centre est retardé).
-en cas d’amétropie hypermétropique, le sommet est dirigé vers l’avant (les bords sont retardés).
-l’existence d’un astigmatisme associé induira une légère asymétrie axiale, particulièrement perceptible au niveau des bords de la parabole de révolution. En cas d’astigmatisme mixte, la forme du front d’onde ressemble à celle d’une chips de type « Pringle ».
-l’existence d’un taux d’aberrations sphériques élevé induit une élongation de la parabole, avec dépression ou voussure localisée de son sommet.
-enfin, la présence d’aberrations de type coma induit une élongation supplémentaire et asymétrique de la parabole.
En présence d’une amétropie sphéro cylindrique, les aberrations de haut degré ont en général un taux beaucoup plus faibles que les aberrations de bas degré (tilt, défocus, astigmatisme). La forme du déphasage qu’elles impriment est en général mieux analysé quand on extrait les aberrations de bas degré de la représentation du front d’onde.

Laisser un commentaire