Topography and longitudinal chromatic aberration characterizations of refractive–diffractive multifocal intraocular lenses. Loicq J, Willet N, Gatinel D. JCRS, 2019

The optical design of multifocal intraocular lenses uses concepts that are sometimes difficult to grasp, especially when it concerns diffractive technology and chromatic aberration control. We published an article (available here) that is based on the optical bench analysis of several models of multifocal diffractive implants to describe their main optical characteristics and report their comparative performances. The underlying goal was to try to correlate the diffractive design of the studied IOL to their optical behavior in terms of power and chromatism.

We have tried to relate these properties to the topographic study of diffractive gratings measured directly on the surface of these IOLs. We hope these results can help clinicians better understand the optical reality of these lenses, which is sometimes blurred by commercial communication and marketing.

Skipping the mathematical details, one can apprehend the diffraction subtleties by learning some relatively simple rules. To illustrate some of the concepts discussed in this article, here are some explanatory diagrams that reflect some of the presented concepts and results. I hope that these illustrations will help the reader to become more familiar with the properties of diffractive IOLs, especially when it comes to chromatism.

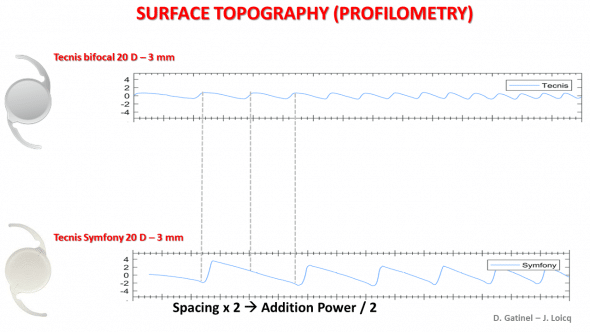
Comparative analysis of the diffractive profile of two lenses can be very instructive as the diffractive profile has a strong impact on the optical properties of a given IOL. As an example, this figure shows two different bifocal IOL topologies:  Tecnis bifocal ZMB00 and the Tecnis Symfony. Topography measurements were acquired using an optical profilometer (Bruker Contour GTI).

The graphs represent the diffractive profiles extracted from the general topology of the IOLs.

Let’s leave aside the difference in height of the diffractive steps for the moment and concentrate on their spacing.

The pitch is inversely proportional to the addition power provided by the diffractive grating. From the depicted harmonic relation between the step widths of the two analyzed IOLs (2 steps on the Tecnis ZMB00 vs one step on the Technis Symfony) one can clearly conclude that the diffractive structure of the Symfony resembles that of a bifocal IOL, and that the addition power of the Symfony is roughly half of that of the ZMB00.

In a previous publication, we have demonstrated that the Symfony, claimed to be an Extended Depth of Focus (EDoF) lens has a diffractive structure providing a power addition of +1.75 D in green light. Again, knowing that the power addition of a diffractive lens is theoretically fixed by the spacing between two consecutive diffractive steps, the number of rings observed on the Symfony is in accordance  with the theory, as 9 rings were been utilized in the case of the EDoF lens, versus more than 20 for the bifocal Tecnis.

Another striking difference is the height of the diffractive steps between these two implants. The Symfony lens has higher steps, which are labeled with the term « echelette » by the manufacturer a semantic choice which could be motivated by the need to differentiate this diffractive grating from competing multifocal diffractive IOLs.

Understanding the consequences of modulating the height of the step of a diffractive pattern is of paramount importance to grasp the chromatic properties of some multifocal IOLs.

The height of the steps governs the amount of light energy distributed on each focus for a given wavelength, and the variation of the refraction index between the IOL and its surrounding medium. The energy associated with a particular focus is linked to the diffraction efficiency of the IOL for the considered wavelength. This efficiency is directly connected to the phase modulation that a considered light undergoes, when it passes through a periodic structure, such as a sawtooth grating, for instance. The phase modulation results from the difference in refractive index for the considered wavelength as it traverses the IOL and surrounding medium (aqueous humor when the IOL has been implanted).

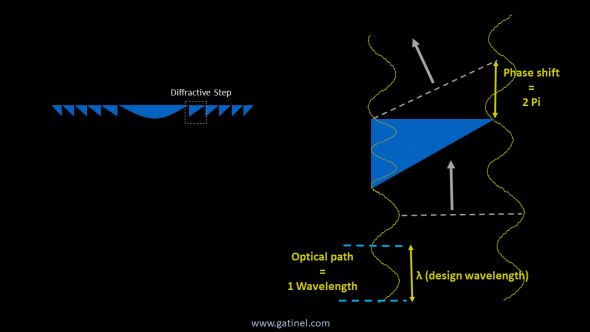
In this example, the phase shift induced by a diffractive step is equal to 2 Pi for the considered wavelength (the equivalent optical path is equal to one wavelength). The maximum constructive interference at the output of the diffractive grating causes the deflection of the incident wavefront towards a single focus (corresponding to the 1st diffraction order). For shorter wavelengths, the phase shift induced by the same step height would be longer than 2 Pi, and this would generate an additional focus corresponding to the 2nd order of diffraction. The focal length of this 2nd order of diffraction would be equal to half of the 1st order foci focal length for that wavelength (the power /vergence would be twice). For longer wavelengths, the phase shift would be shorter than 2 Pi, and this would cause the diffraction of some of this incident light energy in the 0th order of diffraction: in the absence of another optical component, this 0th order diffracted light would not undergo any deviation).

Diffractive optical elements have opposite color dispersion characteristics (i.e different longitudinal chromatic aberration – LCA) than refractive lenses: for a considered focus, the short-wavelength (blue) come into focus after the long-wavelength (red).

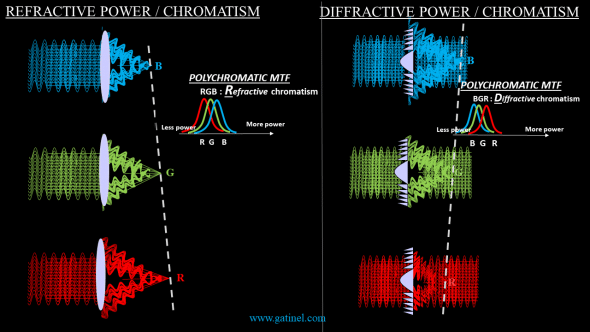
The refractive index of a refractive lens depends on the wavelength considered. It increases for the shortest wavelengths and decreases for the longer wavelengths. For this reason, the blue radiation is focused closer to the lens (has more power) than the red radiation.
For reasons related to the directions in which the constructive interferences, which depend on the wavelength under consideration, the color foci generated by a diffractive process appear in the reverse order than with refractive chromatism. These characteristics make it possible to consider the partial or total correction of chromatic aberration thanks to the combination of refractive and diffractive chromatic dispersion.

The IOL material has a higher refractive index than the aqueous humor; hence, any incremental thickness of the IOL causes some optical path delay or equivalently, a shift in the phase of the considered light wave. For a given wavelength of interest, a phase difference of 2 Pi corresponds to a full-wave difference. If the height of a diffractive step is adjusted so that the phase shift is equal to 2 Pi (one exact wavelength of interest of optical path delay), then all the light energy corresponding to this wavelength will be directed to the 1st order foci.

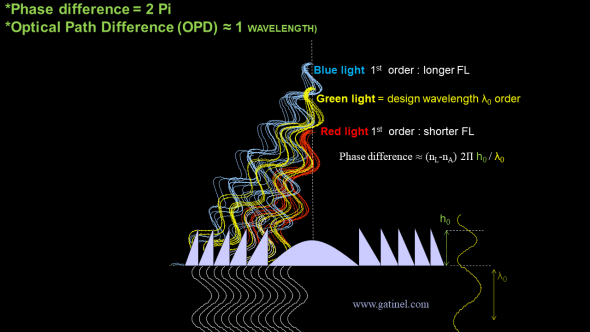
When the height of the steps causes a phase shift equal to 2 Pi (one wavelength) for the green wavelength, it is diffracted in order 1. However, the red (longer) light has also some of its diffracted energy in order 0 (the phase shift is slightly less than 2 Pi), while blue has some of its diffracted energy in order 2 (the phase shift is slightly less than 2 Pi) (these orders are not shown here). For each diffraction order,  the order of the color foci is caused by diffractive chromatism.  
(nL is the refractive index of the IOL material, nA is the refractive index of aqueous humor.)

However, one should note at this stage that a 2 Pi phase shift scenario only applies to the wavelength of interest, which would be presumably of green color (peak of retinal sensitivity) in the context of IOL design. Longer wavelength (between green and the red extremity of the visible spectrum)  undergo a phase shift slightly less than 2 Pi and thus have some energy diffracted in the 0th order, in addition to the 1st order. Conversely, shorter wavelengths (between green and the violet extremity of the visible spectrum) have some energy diffracted in the 2nd order of diffraction as they undergo a phase shift of more than 2 Pi.

Diffracting light into one single diffraction order is not very interesting in the case of a multifocality, as the purported goal of the diffractive design is to split incoming light into several foci. As one can guess, when the height of the step does not match a 2 Pi phase shift, incoming light will be diffracted in multiple consecutive diffraction orders.

When the height of the steps causes a phase shift of less than 2 Pi (half a wavelength in this schematic depiction), the green wavelength is diffracted in order 0 and order 1. The same goes for the other wavelengths, but red is preferentially diffracted in order 0, while blue is preferentially diffracted in order 1. The recombination of the colored radiation in order 0 will be focused at the focal distance of the monofocal carrier lens as if no diffraction occurred: the chromatism of order 0 is refractive in the case of a diffractive intraocular lens whose 0th order corresponds to the far vision foci. The recombination of the colored radiations in order 1 constitutes the total of light energy focused at a focal length that is determined by the spacing of the steps of the diffractive grating and should correspond to a reading addition power in the context of a diffractive intraocular implant for presbyopia correction. The chromatism of the 1st diffraction order is naturally of diffractive type.
(nL is the refractive index of the IOL material, nA is the refractive index of aqueous humor.)

When the phase delay introduced by the height of the diffractive step is longer than 2Pi for the wavelength of interest, the main split occurs between the 1st and 2nd orders of diffraction. Such design incurs higher steps than that of a diffractive IOL diffracting light of the design wavelength in the 0th and 1st orders of diffraction.

When the height of the steps causes a phase shift greater than 2 Pi (3 Pi, about 1.5 wavelengths in this schematic depiction), the green wavelength is diffracted in the order 1 and the order 2. The same goes for the other wavelengths. However, the red (longer wavelength) is a little more diffracted in order 1, while blue is a little more diffracted in order 2.

The extinction of the 0th order of diffraction provides the opportunity to design diffractive multifocal lenses for which all the incoming light is diffracted into the 1st  and higher orders of diffraction.  In these orders, the focal distance of diffracted colors is dictated by diffractive chromatism (nth order diffraction red foci has more power than nth order blue foci), which is opposite to refractive chromatism. This “diffractive chromatism” can be used to compensate for the “refractive chromatism” of the monofocal IOL carrier alone or even the combined refractive chromatism of the cornea and the lens, a claim of the Symfony lens.

The higher steps of the Symfony bifocal EDoF lens are indeed conceived to diffract green light in the 1st and 2nd order of diffraction (phase shift > 2 Pi for green light). In comparison, the lower height of the Tecnis ZMB00 bifocal diffractive steps is designed to split green light evenly between the 0th and 1st orders of diffraction.

These striking difference in the diffractive design explain the differences in the optical behavior and chromatism of the two lenses:

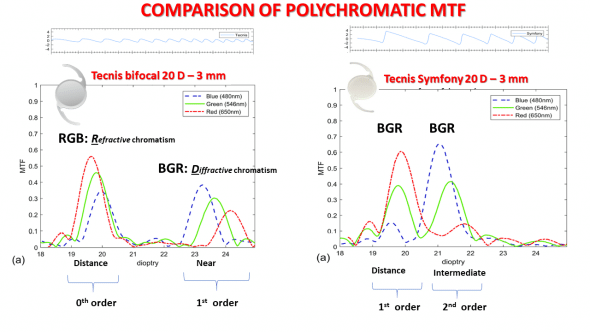
The Tecnis bifocal implant shares the light energy incident mainly between order 0 and order 1. The order 0 is focused thanks to the power of the monofocal carrier lens: the order of the color peaks of the polychromatic MTF curve for that distance focus is dictated by refractive chromatism. Order 1 (focus for near addition) is generated by a diffractive mechanism that causes the order of the peaks of the polychromatic MTF curve to be dictated by diffractive chromatism.
The Tecnis bifocal EDoF Symfony implant shares the light energy mainly between the 1st and 2nd order of diffraction. The 1st order is focused thanks to the power of the monofocal carrier lens AND the addition provided by the diffractive grating. The 2nd order of diffraction creates an addition focus for intermediate vision. The location of the R, G, and B color peaks which combined create the  2 main peaks (distance and intermediate, respectively) of the polychromatic MTF curve of the Symfony is dictated by diffractive chromatism.

The design of the Symfony implies a reduction of the base power of the monofocal carrier, by an amount equal to the addition power of the 1st order of diffraction! The sum of these two powers provides the nominal power of the IOL, for distance vision correction (ex: in a labeled « 22D » power IOL, the monofocal carrier contributes to 20.25D, and the 1st order to 1.75D). The chromatic aberration at this far focus will be dominated by the diffractive nature of the light focusing mechanism, and could compensate for the refractive chromatism brought the cornea.

The improvement of vision quality by LCA reduction has not yet been demonstrated. Although the results were not extrapolated to clinical relevance, we hope that this study still offers the reader a new performance metric to characterize multifocal IOLs and their different foci.

Read the paper for more information about the influence of the material hydrophilicity vs hydrophobicity and trifocality technology capacities on chromatism compensation.