Using Artificial Intelligence and Novel Polynomials to Predict Subjective Refraction. Rampat R, Debellemanière G, Malet J, Gatinel D. Sci Rep 10, 8565 (2020)
Here we present a synopsis of our study, where machine learning using wavefront data processed with a new polynomial decomposition basis is leading to accurate and precise prediction of spectacle correction.
The paper is available here: https://www.nature.com/articles/s41598-020-65417-y
Optical wavefront sensing using aberrometry is an objective method that allows mathematical reconstruction and analysis of lower and higher-order (degree) monochromatic aberrations of the eye. We believe that this objective method had the potential to be the new standard for optimizing the correction of refractive errors by converting aberrometry data to accurate sphero-cylindrical refractions.
The output of a typical wavefront analysis is a list of coefficients, each weighing a specific aberration mode. It is expected that the taxonomy of the higher-order aberrations is clinically relevant and equipped with interesting mathematical properties.
When a wavefront decomposition is performed, each mode is given a coefficient value. The higher the value of the coefficient, the higher the « weight » or effect of the considered mode on the total wavefront error. Wavefront reconstruction over a circular pupil can be achieved by adding some Zernike modes, each weighted by a coefficient whose value is specific to the wavefront of interest.
Various metrics can be derived from the wavefront coefficients analysis:
– The low degree component of the wavefront should correspond to or be highly correlated with the spectacle correction of the measured eye.
– The higher degree component should predict the residual optical defects that persist after correcting that eye with the best spectacles’ correction.
In general, there is a difference between the subjective refraction and the objective refraction predicted by the analysis of the wavefront from the value of the coefficients weighting the low-degree spherical and cylindrical defocus modes. Part of this discrepancy may be related to the influence of high degree aberrations on the subjective perception of the effect of a given low degree correction. The study of the interactions between the best subjective refraction and high degree aberrations is interesting for more than one reason: beyond the prediction of subjective refraction, it also aims to improve the design of personalized refractive corrections and adjust the component low degree refractive with respect to the possible presence of high degree aberrations. Current analyzes are hampered by the fact that the Zernike classification is not suitable for this situation, since certain so-called high-degree aberration modes contain terms of low degree.
Machine learning is already in use in Ophthalmology for image analysis in medical retina and glaucoma as well as regression tasks, notably in IOL calculations.
Our aim was to build and evaluate a set of predictive machine learning models to accurately and precisely objectively refract a patient using wavefront aberrometry with a new aberration decomposition and to evaluate the relative importance of each aberration in the prediction process for each vector.
The accurate distinction between lower and higher wavefront components is mandatory to accurately predict spectacle refraction (as well as accurate retinal image metrics, which was not investigated in this study).
However, Zernike polynomials have one major drawback for describing the ocular wavefront in an ophthalmic context: these polynomials do not accurately distinguish between Lower and Higher Order Aberrations. Lower order terms are present within the expression of some Higher Order coefficients so we can’t accurately predict sphero-cylindrical refraction or accurately define the effects Higher-Order Aberrations on the retinal image viewed.
Thus, the influence of the Zernike spherical aberration Z(4,0) on the spherical cylindrical refraction is essentially linked to the low degree component (defocus) contained in this mode. These characteristics do not allow us to isolate well the specific influence of the high degree component in r4.
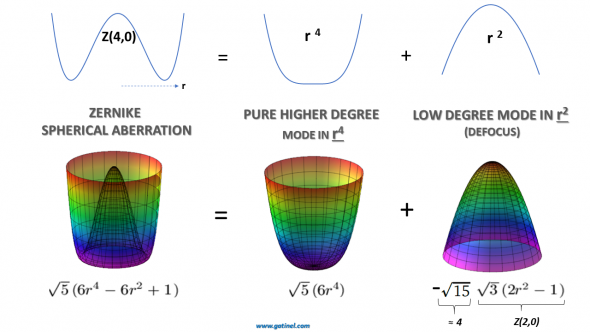
The Zernike spherical aberration mode contains not only a high degree term in r^4 but a low degree term in r^2 which is equivalent to defocus. Each micron of Zernike spherical aberration Z40 contains nearly 4 microns of defocus of opposite sign. If an ocular wavefront is exclusively a r ^4 phase aberration, its reconstruction in Zernike polynomials should automatically include an artifactual defocus component (low degree) to compensate for the defocus necessarily introduced by the Zernike Z(4,0) mode. This mixture does not allow us to simply predict the subjective refraction and study the specific influence of the high degree term in r^4 from a Zernike expansion.
The same goes for high-degree astigmatism Z(4,+/-2), which contains low-degree astigmatism:
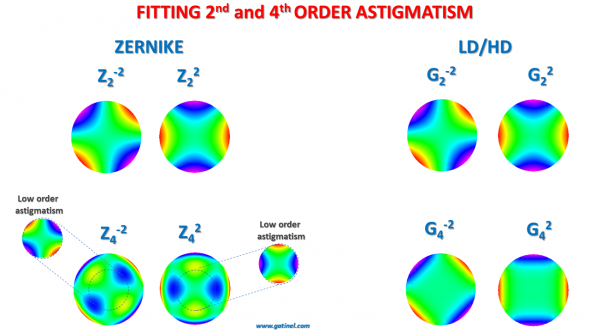
Comparison of the modes aimed at modeling the low and higher degree astigmatism wavefront error. Note the tormented aspect of the higher-order Zernike modes (bottom left) which is caused by the presence of lower-order astigmatism within their analytical expression
Better reconstruction of low order astigmatism would be expected if higher-order astigmatism was devoid of low order astigmatism (bottom right). In eyes with high order astigmatism, this would also allow us to better estimate the specific influence of pure high-order astigmatism on the subjective low-order astigmatism correction.
We have developed a solution to these problems based on new polynomial functions to better distinguish between low degree (LD) and high degree (HD) aberrations: the LD/HD modes expansion. The core of this work has recently been published in the Journal of Optical Society of America (JOSA A), and some relevant clinical examples in the Journal of Refractive Surgery.
We have created new orthogonal and Normalized modes G(n,m) to replace the high order Zernike « impure » modes. Their analytical expression no longer contains low order terms (2 or less), and their central portion is flat.
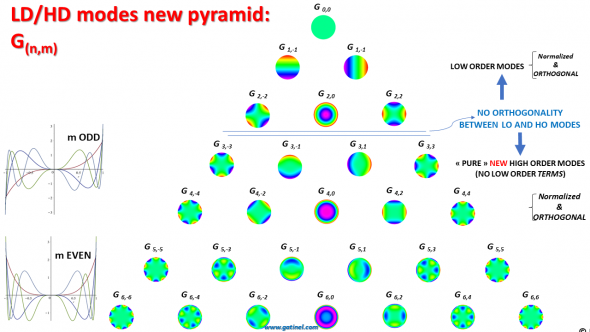
The LD/HD aberration classification proposes a clear cut between low and high-order (degree) aberrations. The higher-degree modes are “paraxially flat” ( cross-sections, left). There is no orthogonality between the LD and HD spaces.
However, orthogonality is maintained between the modes comprised within the low degree and the high degree space. The rupture of orthogonality echoes the clinical approach, which «decouples » the low (spectacle-corrected) and high-order aberrations. It is possible to calculate RMS coefficients of grouped modes within the low and within the high-degree modes. The total RMS cannot be calculated directly from the low degree RMS and high degree RMS values using Pythagorean calculations.
A wavefront error can be decomposed in the LD/HD classification as a sum of weighted G(n,m) modes. The g(n,m) coefficients can be directly computed from the Zernike coefficients z(n,m) without the need for a new wavefront acquisition.
The low order modes G(2,0), G(2-2), and G(2,2) are orthogonal and their respective coefficients can be easily converted in the 3D dioptric vector space components of the refraction M, J0, and J45.
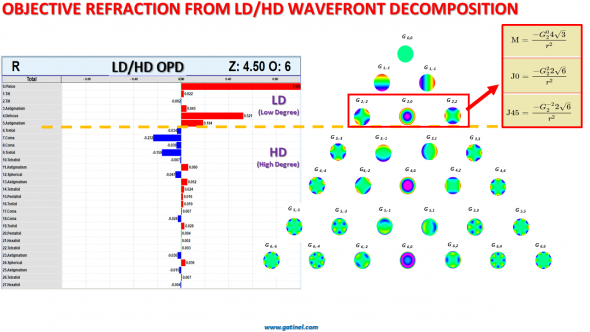
In the LD/HD decomposition, no low degree term is present in the high degree modes. All the terms corresponding to 2nd degree spherical and cylindrical defocus are gathered in the low degree component (LD). The low order coefficients of the 2nd radial degree mode of the LD/HD classification can be converted in the vector components of the refraction (r is the radius of the pupil). This comprehensive 2nd degree component is equivalent to an osculating quadric to the wavefront and can serve to compute an objective “paraxial refraction”. However, this objective refraction, although close to the subjective refraction, often differs slightly from this one on an individual basis.
The remaining high degree component is devoid of low degree terms e.g. defocus and 2nd-degree astigmatism. This allows unequivocal analysis of the influence of the high-order aberrations on the subjective spectacle low order correction.
A total of 2890 electronic medical records of patients (6397 eyes) evaluated for refractive surgery at the Laser Vision Institute Noémie de Rothschild (Foundation Adolphe de Rothschild Hospital, Paris) were retrieved and analyzed. For each eye, the following data was available:
– Non-cycloplegic subjective refractions: Each refraction in Sphere S, Cylinder C, and axis A format was transformed into 3D dioptric vector space (M, J0, J45) where the three components are orthogonal.
– Wavefront analysis: obtained using the OPD-Scan III (Nidek, Gamagori, Japan) aberrometer specially configured to run using beta-software incorporating the new series of LD/HD polynomials up to the 6th order.
A machine learning approach using LD/HD polynomials was developed for predicting the results of conventional, sphero-cylindrical refraction from wavefront aberrations.
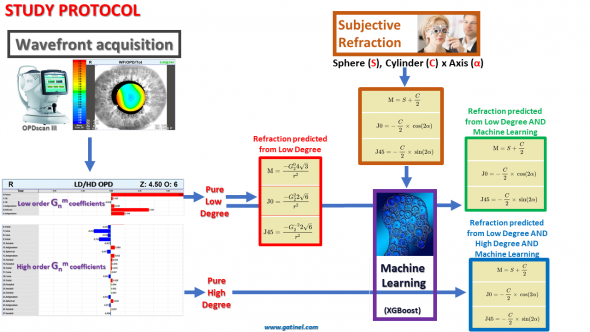
Diagram summarizing the study protocol: the machine learning algorithm was trained to predict subjective refraction components using low +/- high degree G(n,m) wavefront coefficients from the LD/HD expansion.
XGBoost is an implementation of gradient boosted trees focused on performance and computer efficiency. It can perform both regression and classification tasks. It was chosen because of its recognized performances and its resistance to overfitting.
Feature importance analysis was achieved via the calculation of SHAP (SHapley Additive exPlanations) values for each model in order to determine the most influential polynomials.
Read this paper to learn how the best precision and accuracy were obtained, when all the novel polynomials coefficients were used as predictors, demonstrating the significant influence higher-order aberrations have on spectacle correction.
I wish to thank the co-authors who have contributed to this work: Guillaume Debellemanière (MD), Radhika Rampat (MD), and my Ph.D. directors: Laurent Dumas (Ph.D.), and Jacques Malet (Ph.D.).
I also wish to thank the Nidek company and its R&D team for implementing this new method in a beta-software, now able to process wavefront data obtained with our OPD-Scan III wavefront sensor.
More pages on this website about wavefront sensing and analysis:
Novel wavefront decomposition method
Novel wavefront decomposition method: clinical analysis
Pre and post LASIK aberrations


FULLZ USA UK CANADA
SSN NIN SIN with NAME DOB ADDRESS
High Credit Scores Pros
CC with CVV
Dumps with Pin codes Track 101 & 202
Real DL|ID Front Back with Selfie
Passport Photos
Business EIN Company Fullz
Young Age fullz 2002 Above
Fullz for UberEats|SBA|PUA|UI|DoorDash|KYC
Spcific info you can get Cities|States|Gender|ZipCodes
Carding|Loan Methods & Tutorials
Spamming|Scripting Tools & Tutorials
Scam Pages|Shells|C-panles
Senders|Mailers
RDP|SMTP
& many other fresh stuff available
Valid & Legit stuff will be provide
NO refund|Only Replacement
Payment mode crypto Currencies
CONTACT:
ICQ 752822040 ‘ (at)killhacks
Tel Gr (at)leadsupplier ‘ (at)killhacks
Email Bigbull0334 (at) onion mail . org
Good read. I learnt French in school back in the day.
tildaloch@mein-handwerk.net
Get your ex lover back no matter why he left you.
My boyfriend that left me a few months ago just came back to me last night crying for me to take him back. After a 3 year relationship with my boyfriend, he changed suddenly and stopped contacting me regularly, he would come up with excuses of not seeing me all the time. He stopped answering my calls and my sms and he stopped seeing me regularly. I then started seeing him with different girls several times but every time he would say that he loved me and that he needed some time to think about our relationship. But I couldn’t stop thinking about him so I decided to go online and I saw so many good talks about this spell caster called Dr Kadiri and I contacted him and explained my problems to him. He cast a love spell for me. and After 11hours, my boyfriend came back to me and started begging me to forgive him. We moved in together after a few months and he was more open to me than before and he started spending more time with me than his friends. We eventually got married and now have been married happily with a son. Ever since Dr Kadiri helped me, my boyfriend is very stable, faithful and closer to me than before, You can also contact this spell caster and get your relationship fixed .Here’s his contact, WhatsApp him: +2348102430456 or Email him at: drkadirilovespellhome@gmail.com
I rarely write reviews, but I had to for this! Because I tried several apps to help with no luck. Back then, I was very confused and always felt awful about my partner’s cheating attitude. I really wanted to track and catch him red-handed. I downloaded this app hoping it would help but I wasn’t satisfied with its features as I needed to monitor my partner closely. I then spoke with a trusted colleague of mine at work and she gave me a genuine recommendation about an ethical private investigator named Michael Calce Wizard, I wrote to his email at michaelcalcewizard78@gmail.com explaining how I wanted to have complete access to his call log, iMessage/SMS, social media activities, gallery, texts, deleted or not, his precise location day in day out. I paid for his services and in about 2-3 hours, I had complete access to his phone. I got concrete evidence. it was unbelievable to see the evidence of cheating on me. Who likes to live with a cheater, I used the evidence I got to file for a divorce. I’m thankful to Michael Calce Wizard for helping me out of my dilemma and suspicions. His services are highly rated and affordable. If you are having trust issues and need valid evidence, how about you contact michaelcalcewizard78@gmail.com. Thank you Michael Calce Wizard for an incredible job !! I highly recommend his services, simply the best.
Contact : michaelcalcewizard78@gmail.com
WhatsApp Number : +447375542502