Acuité visuelle et dimensions de l’image rétinienne
Quelle est la taille de l’image rétinienne d’un objet vu par l’œil ? Cette question est importante pour comprendre les facteurs limitant l’acuité visuelle, et certaines conséquences de la chirurgie réfractive, en particulier pour les fortes amétropies. Le caclul de la taille de l’image rétinienne est également important pour les problèmes liés à la différence de taille des images rétiniennes (anéisoconie). Une différence excessive de la taille des images rétiniennes entre les yeux droit et gauche d’un même sujet peut induire une disparité excessive et des troubles de la vision binoculaire, avec réduction de la perception du relief (stéréoscopie).
Si la densité, la taille des photorécepteurs de la fovéa varie d’un oeil à l’autre, il est évident que pour une même densité de photorécepteurs (capacité d’échantillonnage), la résolution rétinienne sera d’autant plus importante que l’image projetée sera grande.
Dimensions de l’image rétinienne d’un objet situé à l’infini
Ce problème peut être généralisé à celui d’n système optique quelconque, dont on connait la puissance globale (appelée D, en dioptries). Ce système forme dans des conditions paraxiales l’image d’un objet situé à l’infini dans son plan focal image. La hauteur de cette image est T’. Voici comment la calculer :
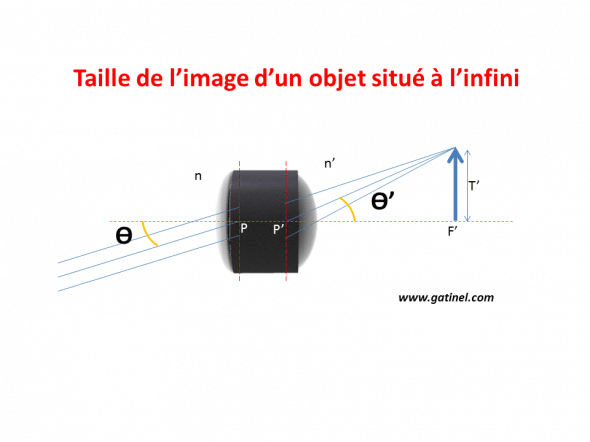
La taille de l’image formée par un système optique d’un objet situé à l’infini peut être calculée si l’on connait l’angle qu’il sous tend avec le système (lui même dépend de la taille de l’objet et sa distance avec le système optique), et la puissance du système optique.
La figure ci-dessus permet d’établir (en exprimant ces distances en mètres, et les angles en radians)
T’= ϴ’ P’F’
En utilisant l’équation paraxiale (pour de petits angles), on peut aussi poser :
n ϴ =n’ ϴ’ (n et n’ sont les indices de réfraction des milieux objets et image)
Ainsi, T’= (n/n’) ϴ P’F’
Par ailleurs, D = n’ / P’F’, donc P’F’ = n’/D
On obtient au final : T’ = n ϴ / D
Cas de l’œil :
Le milieu d’observation habituel de l’œil est l’air, donc n= 1.
On obtient ainsi une formule simple : T’ = ϴ / D qui établit que les dimensions de l’image rétinienne d’un objet qui sous-tend un angle ϴ est égal au rapport de cet angle avec la puissance équivalente de l’œil. On choisit généralement une valeur arrondie de 60 D pour le pouvoir réfractif équivalent de l’œil (cornée + cristallin).
Pour un angle d’une minute d’arc (exprimé en radian), et une puissance oculaire de 60 D, on obtient que la taille T’ de l’image rétinienne est égale à 0.004850 mm soit environ 5 microns. Pour séparer deux points qui forment un angle d’une minute d’arc avec l’œil, il faut 3 photorécepteurs, soit un espace entre le centre de ces photorécepteurs de 2.5 microns (deux photorécepteurs sont stimulés, et séparés d’un photorécepteur non stimulé).
Certaines études montrent que la taille minimale des cônes de la fovéa peut être inférieure de moitié à cette valeur (1.7 microns environ), et ceci explique que l’acuité visuelle de résolution (pouvoir séparateur) puisse atteindre 30 secondes d’arc (une demi minute d’arc, soit 20/10 environ).
Effet des moyens de correction des défauts optiques sur la taille de l’image rétinienne
Dans l’exemple précédent, nous avons considéré un œil emmétrope.
Pour un œil amétrope simplifié, la taille de l’image rétinienne varie avant et après correction de l’amétropie, qui peut être accomplie par un verre de lunettes, une lentille ou une chirurgie photoablative.
Pour un objet situé à l’infini, on peut établir que le grossissement (grossissement ou « magnification ») ou le rétrécissement (réduction) de la taille de l’image (on appelle ce facteur GV) induit par un verre de lunette est lié au rapport :
GV = Taille de l’image après correction (nette) / Taille de l’image avant correction (floue)
Ce rapport est également celui des angles que sous-tendent les objets vus avec et sans correction vis à vis du centre pupillaire. Exprimé en taille angulaire, ce rapport devient :
GV = ϴ’/ ϴ
Prenons l’exemple d’un œil hypermétrope, pour lequel l’image se forme en arrière de la rétine.
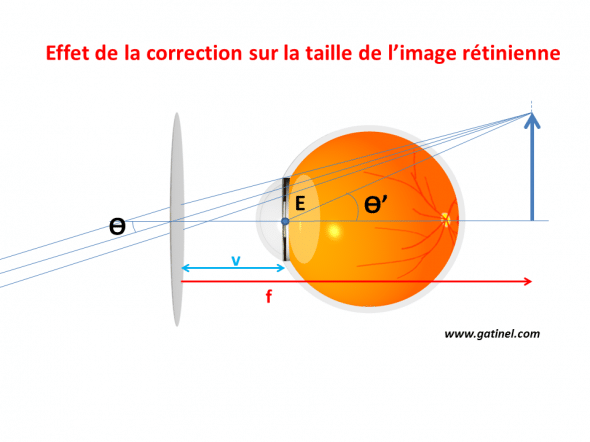
L’objet sous-tend avec l’œil hypermétrope un angle ϴ avec la pupille d’entrée de l’œil (il s’agit de la taille angulaire apparente). L’œil corrigé « voit » l’objet correspondant à l’image formée par la lentille correctrice, sous un angle ϴ’. Le rapport de ces angles permet de calculer l’effet induit sur la taille de l’image rétinienne par la correction optique.
Pour cet œil amétrope non corrigé, en utilisant la formule donnant la taille de l’image en fonction de l’angle sous-tendu par l’objet, on obtient:
T’= ϴ/D, où ϴ est l’angle formé avec l’axe visuel pour un rayon passant par la pupille d’entrée. Cette image est floue, car l’oeil est amétrope et non corrigé.
Avec un verre de lunette convexe correcteur, l’œil devient emmétrope, car le verre focalise les rayons parallèles captés de l’objet dans le plan du verre convexe (qui correspond au punctum remotum de l’oeil hypermétrope). En effet, l' »action » d’un verre correcteur pour l’hypermétropie (et la myopie) est de focaliser les rayons émis par les objets éloignés dans le plan du punctum remotum de l’oeil amétrope. Ils y forment une image virtuelle que l’oeil amétrope « voit » alors nette, sans effort (le punctum remotum correspond à la distance à laquelle doit se situer un point pour être imagé sur la rétine d’un oeil amétrope).
Dans le cas de l’oeil hypermétrope, ce punctum remotum est un plan situé en arrière de l’oeil. l’angle du rayon émergent de cette image « virtuelle » passant par le centre de la pupille d’entrée est noté ϴ’. Cet angle est celui de l’objet vu par l’oeil (cet objet est donc l’image virtuelle formée par le verre correcteur).
D’après la géométrie de l’image, cet angle peut être calculé comme suit :
ϴ’ = T’ / (f – v) où v est la distance du verre au centre de la pupille.
On obtient donc, en remplaçant ϴ et ϴ’ par les expressions calculées:
GV = T’/ (f-v) T’ D, ou, après simplifications :
GV = 1 / (1 – vD)
Cette expression fait intervenir la distance du verre correcteur (v), et sa puissance (D)
Pour un œil myope : D<0, donc GV < 1 : la taille de l’image est réduite.
Pour un œil hypermétrope : D >0, donc GV >1 : la taille de l’image rétinienne est augmentée.
Ces effets seront d’autant plus marqué que v est grand.
Exemples de modification de l’image rétinienne des verres correcteurs et conséquences pratiques
Oeil myope
Un oeil myope est corrigé par un verre de 3 dioptries placé à 12 mm de l’oeil, quel est le pourcentage de réduction de la taille de l’image rétinienne?
Il faut calculer la distance du verre au centre de la pupille d’entrée de l’oeil simplifié: celle-ci est située à environ 3 mm du sommet de la cornée, donc v = 15 mm (= 0.015 m). On calcule GV=95%, soit une réduction de 5% de l’image rétinienne en taille. Une telle différence peut induire une difficulté à fusionner les images si l’autre oeil est emmétrope (verre plan). A l’inverse, la réalisation d’une chirurgie réfractive, délivrée dans le plan cornéen (LASIK ou PKR) permet (comme en lentilles de contact) de « grossir » l’image focalisée sur la rétine, et d’obtenir un gain au moins théorique en acuité visuelle.
Ce gain est particulièrement intéressant pour la correction de la myopie forte en LASIK, ou en chirurgie de la cataracte. L’illustration suivante représente l’effet d’un verre correcteur pour myopie forte (-29 Dioptries en lunettes). La longueur axiale de l’œil est de 33 mm.
La correction du verre n’est taillée qu’au sein d’une portion centrale circulaire, de manière à amincir les bords du verre et améliorer l’esthétique de la monture portée. Les bords du verre ont une puissance nulle.
Un cliché pris à faible distance (2 cm) avec un smartphone permet de comparer la taille de l’image transmise après réfraction par le verre correcteur de -29 D. Le calcul du grandissement théorique du verre de -29 D est égal à 63% (en supposant que l’écran soit « à l’infini »). Cette réduction correspond à peu près à celle qui est observée sur le cliché (au centre). On peut estimer qu’une correction de cette myopie par une chirurgie du cristallin (remplacement du cristallin par un implant destiné à emmétropiser ou laisser une faible myopie) permettrait un gain proportionnel en taille de l’image projetée sur la rétine, et donc un gain significatif de la meilleure acuité visuelle corrigée.

Effet de réduction de la taille de l’image transmise par un verre fortement concave pour la correction d’une myopie de -29 Dioptries dans le plan lunettes. Le calcul théorique prédit une réduction d’environ 65%, conforme à ce qui est observé. A gauche, mesure au fontofocomètre de la puissance du verre, au centre cliché d’un écran d’ordinateur pris à 2 cm au travers du verre correcteur (noter l’effet de réduction de l’image et l’effet prismatique du verre fortement concave). En haut à droite, le cliché est pris à plus grande distance du verre, ce qui accentue l’effet de réduction de l’image. Au droite au centre, port de l’équipement optique par le sujet fortement myope
Oeil hypermétrope
Un oeil hypermétrope est corrigé par un verre de 6 Dioptries, placé à 12 mm de l’oeil.
v = 15 mm , et GV = 1,10 soit une augmentation de 10% de l’image rétinienne en taille.
Ces effets de modification de taille des images sont faciles à percevoir au travers de verres de lunettes pour un emmétrope L’image vue est « floutée » par la correction qui introduit une défocalisation, mais elle est plus petite au travers d’un verre concave correcteur de myopie, et plus grande au travers d’un verre convexe correcteur d’hypermétropie.
Ces pourcentages peuvent sembler modestes, mais ils peuvent atteindre des valeurs plus élevées pour les fortes amétropies, comme la myopie forte. Par exemple, pour une myopie de 16 D, la correction en lunettes induit une réduction de 20% de la taille de l’image rétinienne (par rapport à la taille de l’image floue, du même oeil non corrigé). On peut établir de manière symétrique qu’une correction dans un plan plus proche du centre pupillaire (lentille, ou chirurgie réfractive cornéenne) peut induire un « grossissement » de l’image rétinienne vis à vis de l’image nette en lunettes (correction de la myopie). La correction dans le plan de la pupille est accomplie en cas de chirurgie de la cataracte, puisque l’on remplace le cristallin par un implant).
Un grossissement de l’image rétinienne de 15% à 20 % est bénéfique car il permet à la rétine de mieux échantillonner l’image formée: Le gain attendu en terme d’acuité visuelle est significatif car la réduction de l’angle minimum de résolution (MAR) est du même ordre. Ceci est d’autant plus bénéfique car certaines études montrent que les forts myopes ont une capacité d’échantillonnage rétinienne moins élevée que les emmétropes (plus faible densité de photorécepteurs au niveau de la fovéa). Ainsi, un myope fort de 16 Dioptries dont la meilleure acuité visuelle corrigée en lunettes est de 8/10 (MAR =1,25 minute d’arc) bénéficie d’une acuité visuelle en lentilles de 10/10 (MAR = 1 minute d’arc). Cette différence est bien entendue accentuée pour les myopies encore plus fortes.
Ainsi, la correction de la myopie forte permet une meilleure acuité visuelle quand elle est effectuée par un système proche de l’oeil (lentille, chirurgie réfractive cornéenne, implant intra oculaire).
Ces modifications de la taille de l’image s’accompagnent d’autres phénomènes comme des variations du champ de vision apparent, qui est plus étroit en lentille qu’en lunettes.
En revanche, l’hypermétrope fort possède une acuité visuelle légèrement meilleure en correction lunettes, puisque l’image est « grossie » sur la rétine. Ceci s’accompagne d’une réduction du champ visuel apparent.
Enfin, on peut montrer que si l’existait une technique de correction consistant à avancer ou reculer la rétine pour corriger l’amétropie (avancer vers la cornée pour les myopes, et reculer la cornée pour les hypermétropes), alors la taille de l’image rétinienne serait la même une fois l’oeil corrigé que celle qu’il avait auparavant avec un verre de lunettes (situé à environ 16 mm du plan principal objet de l’oeil).
La correction de l’astigmatisme implique une modification de la taille de l’image qui varie avec l’azimut ! Ceci explique pourquoi les lignes droites observées au travers de verres toriques (cylindriques) correcteurs semblent subir une légère « rotation », un changement d’inclinaison.

Bonjour Dr, suite à votre article de 2016 très technique, je me permets de soumettre mon cas : suite au changement d’un implant défectueux (opacité 100%) je me retrouve avec un œil légèrement myope et une image rétrécie en largeur (environ 15% à mon avis). On me dit que le cerveau va s’habituer mais 2 mois après l’opération je ne note pas de changement. C’est gênant pour conduire d’autant que l’autre œil (directeur) est atteint d’une légère DMLA. Qu’en pensez-vous. Est-il possible de corriger ? Cordialement. JJC
NB en temps qu’ancien pilote de chasse, ma vue était parfaite. Maintenant j’ai 81 ans.
Si les efforts de correction ont été suffisant, et que votre acuité visuelle demeure limitée à 8/10, il est effectivement possible que ceci soit lié à une moindre densité ed photorécepteurs au niveau de la fovéa, ce qui a été montré pour les yeux myopes forts. Par ailleurs, la réduction de la taille de l’image rétinienne provoquée par les verres de correction de la myopie forte pourraient également expliquer cette moindre acuité. L’acuité visuelle en correction lentille, LASIK (quand celui ci est possible), ou implant intraoculaire permet souvent de gagner une ou deux lignes d’acuité visuelle, en raison de l’augmentation de la taille de l’image refocalisée sur la rétine (vis à vis de celle qui est obtenue en correction lunettes). Un test en lentille de contact correctrice pourrait confirmer ce point.
Bonjour et merci pour cet article très intéressant.
Etant myope forte, je suis corrigée au maximum à 8/10 en lunettes et ce depuis l’enfance (ma myopie étant bien moindre à l’époque), et ce sans problème rétinien, amblyopie ou strabisme.
Est-ce nécessairement du à un problème de photorécepteurs, ou bien à une mauvaise adaptation de lunettes?
Merci!