Pouvoir optique paraxial de la cornée
Calcul du pouvoir optique (vergence) de la cornée
Le pouvoir optique paraxial ou vergence de la cornée dépend de la courbure de ses faces avant et arrière, ainsi que de son épaisseur.
Que cherche-t-on ?
A déterminer la vergence (pouvoir optique) de la cornée entière (effet conjugué de la réfraction des faces avant et arrière). On souhaite à déterminer un modèle paraxial de la cornée, ce qui implique la détermination de la position des plans principaux, et des distances focales, comme pour une lentille épaisse (voir la page consacrée à la justification de l’optique paraxiale et des plans principaux)
Que connait-on ?
La topographie de la cornée permet de mesurer les courbures apicales de la cornée, et il est possible d’obtenir l’épaisseur par une mesure tomographique.
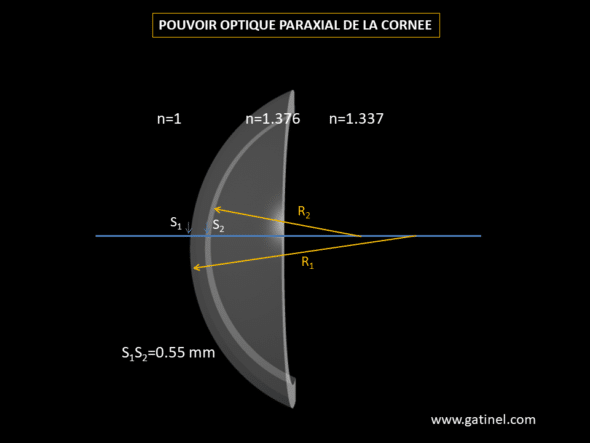
On connait la valeur de l’indice de réfraction du stroma cornéen (nco = 1.376, et de l’humeur aqueuse (nhaq=1.337 ou 1.336)
La courbure antérieure possède un rayon R1 = 7.8 mm
La courbure postérieure possède un rayon R2 = 6.5 mm
L’épaisseur eco = S1S2 = 0.55 mm
Représentation des données dont on connait les valeurs numériques pour le calcul de la puissance paraxiale de la cornée.
Calcul de la puissance de la face avant de la cornée
D1 = (nco – 1)/R1 = (1.376 -1)/0.0078 = 48.21 D
Distances focales face avant
La distance focale objet est donnée par f1 = -1/48.20 m = -0,02074 m
La distance focale image est donnée par f’1= 1.376/48.21 m = 0.02854 m
Calcul de la puissance de la face arrière de la cornée
D2 = (nhaq – nco)/R2 = (1.337 -1.376)/0.0065 = -6.0 D plus la cornée est cambrée (R2 diminue), plus la face postérieure fait « diverger » les rayons lumineux!
Distances focales face arrière
La distance focale objet f2 = -1.376/-6.0 m = 0,2293 m
La distance focale image f’2 = 1.337/-6.0 m = -0,2228 m
L’étape suivante est de calculer la puissance du système centré équivalent à la cornée (Dco), en tenant compte de l’épaisseur de la cornée au centre (distance entre la face antérieure et la face postérieure).
Puissance du système centré équivalent à la cornée (Dco)
On utilise pour cela la formule de Gullstrand, qui concerne les systèmes « épais » : on retranche à la somme des termes de puissance le produit de l’épaisseur par les puissances avant et arrière divisé par l’indice de réfraction du stroma.
Dco = D1 + D2 – eco(D1D2)/ nco = 48.21 -6.15 –0.00055 x 48.21x-6.15/1.376 = 42.32D
La distance focale objet de la cornée (face avant et face arrière) est égale à fco = -1/ Dco = -1/42.32 m = -0,02362 m
La distance focale image de la cornée est égale à f’co = 1.337/ Dco = 1.337/42.32 = 0.03158 m
Il reste à déterminer la position des plans et points (intersection des plans avec l’axe optique) principaux de la cornée.
Position des plans principaux de la cornée
La distance entre (point) plan principal objet Hco et le sommet de la cornée S1 est:
S1Hco = eco fco / f2 = 0.55 x ( -23.62) / (222.8) = – 0.0583 mm
La distance entre (point) plan principal image H’co et le sommet de la cornée S2 est:
S2H’co = -eco f’co / f’1 = -0.55 x ( 31.58) / (28.54) = – 0.6085 mm
(des pages sont consacrées à la modélisation paraxiale d’une lentille épaisse et aux explications et calcul des la position des plans et points principaux d’un système paraxial)
Le signe négatif des distances correspond à une position du plan principal objet située en avant de la cornée (58.3 microns avant S1). La position du plan principal image est également située à 0.55-0.6085 = 0.0585mm environ 60 microns en avant de la face avant S1.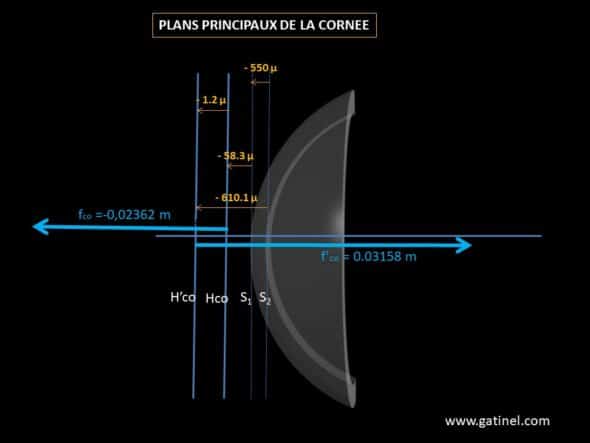
Position des plans principaux de la cornée (les distances ne sont pas à l’échelle)
Conclusion
L’écart entre les plans principaux de la cornée est très faible (1.8 microns), et la distance avec le sommet de la cornée (vertex en S1) est négligeable.
On peut assimiler le comportement optique paraxial de la cornée à celui d’un dioptre sphérique. Un tel dioptre aurait une courbure telle que :
R = (1.336-1)/42.17 = 7.97 mm.
Le même calcul peut être effectué pour le cristallin (voir calcul de la puissance paraxiale du cristallin). Le cristallin n’est pas assimilable à un dioptre sphérique, et le calcul de ses propriétés paraxiales correspond à celui effectué pour une lentille épaisse.
Conséquences: approximation du pouvoir optique de la cornée
Le rayon calculé avec la formule du dioptre sphérique est relativement proche du rayon de courbure antérieur « réel » de la cornée (7.8 mm). L’indice considéré est comme il se doit pour ce calcul est celui de l’humeur aqueuse (n=1.336). Si l’on choisit une valeur un peu plus réduite pour cet indice (ex : n =1.333), on obtient une valeur encore plus proche de la valeur initiale du rayon de courbure antérieur.
Cette approximation correspond à l’utilisation d’un indice dit « minoré » ou kératométrique, utilisé sur les kératomètres et dans le logiciel des topographes pour calculer les cartes de puissance (on devrait dire courbure) axiale et tangentielle en dioptrie. L’intérêt de cette approximation était lié à l’impossibilité de mesurer la face postérieure de la cornée de manière aisée en pratique clinique. Elle fournit d’ailleurs une estimation suffisamment précise de la puissance kératométrique en dioptries pour la plupart des applications courantes.
Toutefois, elle n’est valide que pour les cornées dont l’effet de la courbure postérieure sur la puissance antérieure ne diffère pas trop de la « moyenne ».
Par exemple, si l’on mesure une valeur de rayon de courbure de 8.5 mm (cornée plate, après LASIK ou PKR myopique), mais que l’on conserve la même valeur de courbure postérieure (6.5 mm), le calcul de la puissance paraxiale en utilisant les équations précédentes fournit la valeur suivante : Dco = 38.2 D.
En utilisant l’approximation avec n=1.333, on obtient une puissance paraxiale égale à 39.2 D : une erreur de 1D (surestimation) peut avoir des conséquences cliniques non négligeables. Il est ainsi déconseillé d’utiliser cette approximation (cornée = dioptre sphérique avec indice minoré) après chirurgie réfractive pour réaliser un calcul biométrique, et ce d’autant plus que les autres imprécisions de mesure de la kératométrie tendent après chirurgie réfractive à surestimer la puissance cornéenne centrale… ce qui induit une sous-estimation de la puissance de l’implant à poser et risque d’induire une hypermétropie après chirurgie de la cataracte.
La position de l’implant (après insertion dans le sac capsulaire qui s’effectue lors de la chirurgie de la cataracte) peut varier pour des raisons qui tiennent à la géométrie de l’oeil opéré (profondeur de la chambre antérieure, comportement de l’implant dans le sac capsulaire, etc.). Dans un modèle paraxial de l’oeil « pseudophake », qui associerait cornée et implant, la position effective de l’implant correspond à la distance entre le plan principal image de la cornée, et le plan principal objet de l’implant.
Enfin, dans un calcul paraxial (calcul biométrique paraxial par exemple), la longueur « optique » de l’oeil n’est pas tout à fait égale à la longueur anatomique : il faut en effet faire débuter la longueur de l’oeil au niveau du plan principal objet, qui est situé environ 50 microns en avant de la cornée. Ceci explique le terme « +0.050 » (en millimètres) qui est souvent ajouter à la longueur axiale (L), mesurée dans les formules biométriques (ex: formule de Colebrander).
Grâce au calcul des puissances focales et de la position des éléments cardinaux de la cornée, on peut calculer la puissance optique de l’oeil entier.

Laisser un commentaire